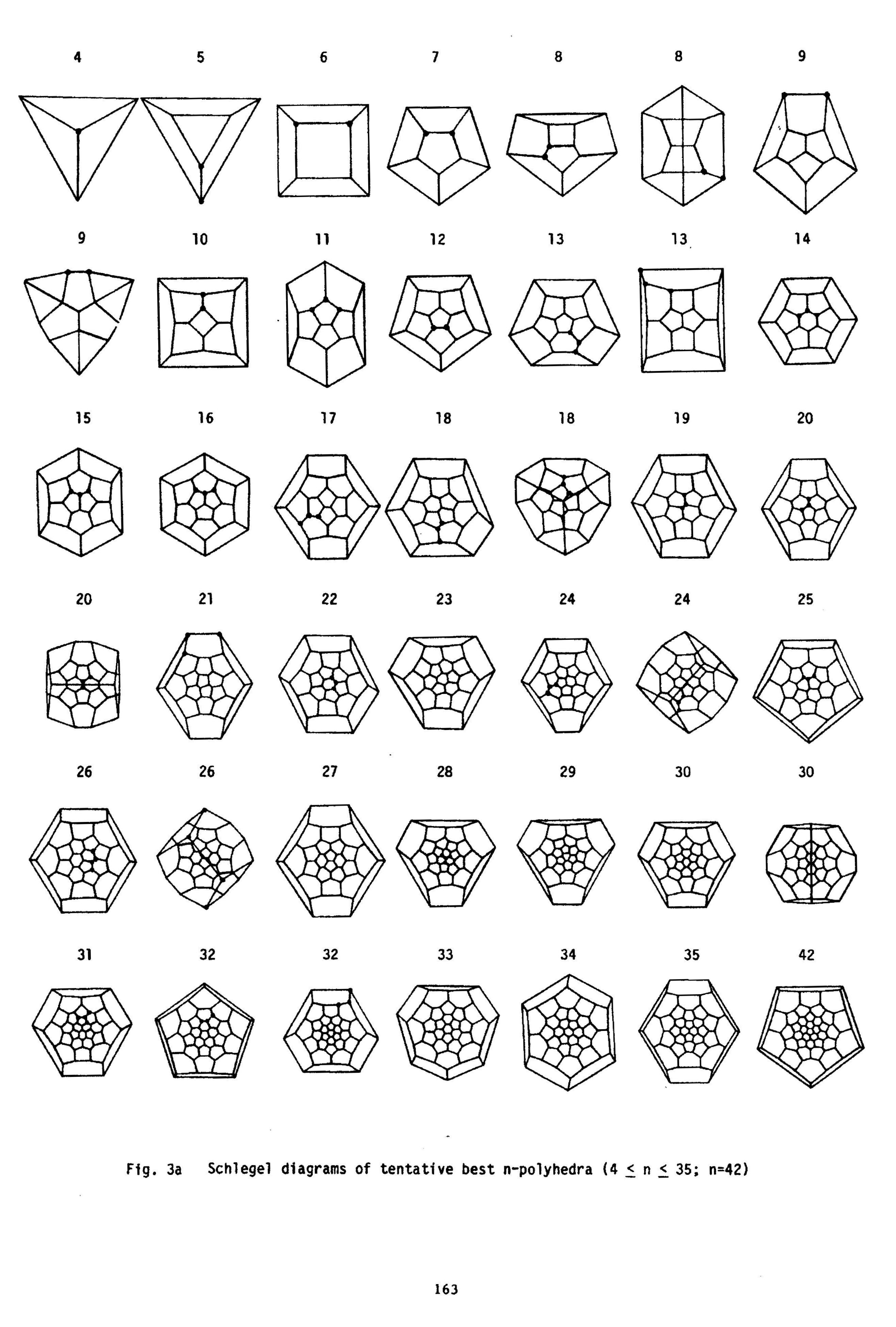
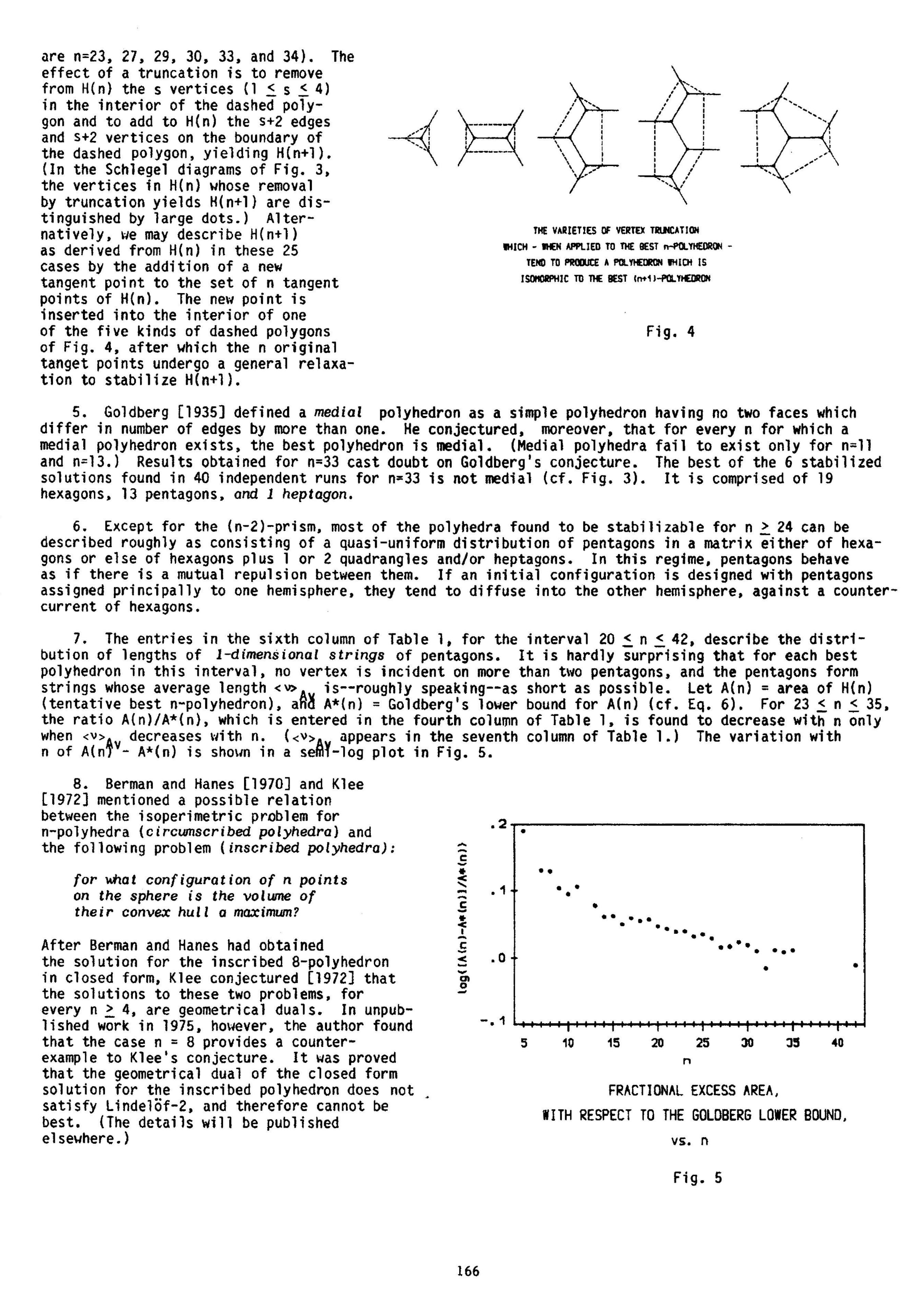
ROUNDEST POLYHEDRA
Alan H. Schoen

Comments are welcome!


Nested pair of truncated icosahedra, (sculptor unknown)
Photographed by Reiko Takasawa Schoen in Madison
Square Park, New York City, October 21, 2012

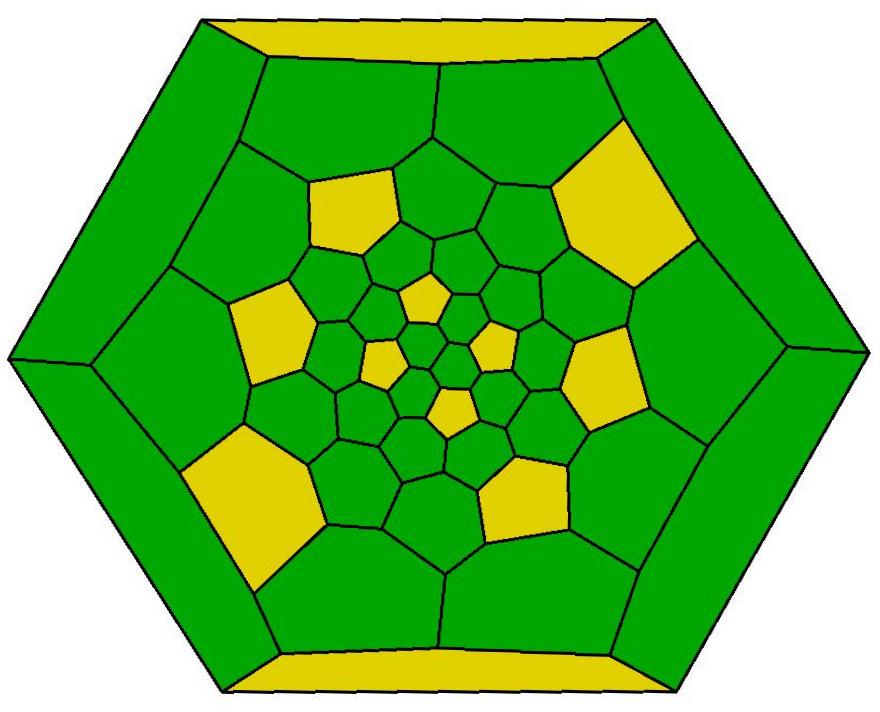
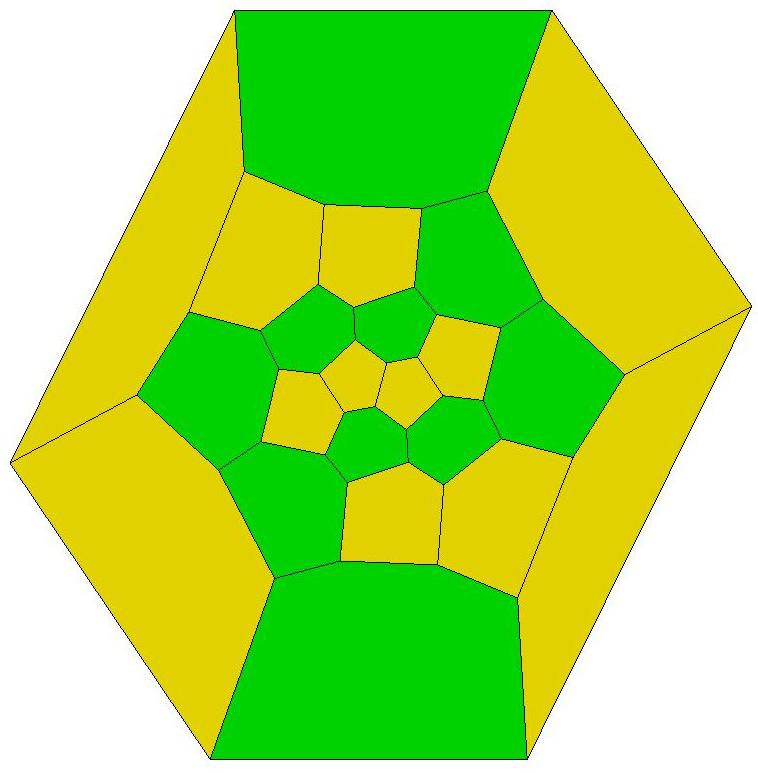
The fifteen convex cells in this packing are the Voronoi polyhedra of
fifteen points located at random positions in the central region of a sea
of more than one hundred random points. The computer program used
to carry out the calculations was designed by the author and was coded
in FORTRAN by Randall Lundberg in 1969. In 1971, Robert Fuller
constructed this vinyl model.
I DREW MOST OF THE COMPUTER
IMAGES BELOW USING COORDINATE
DATA PROVIDED BY WAYNE DEETER.
I THANK HIM FOR HIS GENEROSITY!
A1. Roundest Polyhedra
The theory of roundest polyhedra
(sometimes called best polyhedra)
was first treated by
Simon Antoine Jean L'Huilier
(1750-1840). One
of several accomplishments for which L'Huilier is remembered today
is his generalization
to non-convex polyhedra of the famous formula
of Euler for convex polyhedra,
which Euler first described in 1750 in
a letter to Goldbach:
v, e, and f are the numbers of vertices, edges, and faces, respectively.
The history of this development is summarized in
George G. Szpiro's
fascinating book, "Poincaré's Prize".
Mathematicians refer to the subject of roundest polyhedra as
'The Isoperimetric Problem for Polyhedra'.
In the 19th century the theory
of roundest polyhedra was investigated
by
Jakob Steiner, E. Kötter, Lorenz Lindelöf, and Hermann Minkowski,
and in the 20th century by Ernst Steinitz,
Michael Goldberg, and Victor Klee.
Lorenz Lindelöf proved a fundamental theorem
about roundest polyhedra
(cf.
my 1986 conference paper)
— first in 1869 and again in 1899. In 1986
Klee greatly deepened the analysis and extended it to dimensions beyond three.











Jakob Steiner (1796-1863)
Lorenz Lindelöf (1827-1908)
Hermann Minkowski (1864-1909)



Georgy Voronoy (1868-1908) Ernst Steinitz (1871-1928) Victor Klee (1925-2007)
In 2011, Ms. Ivonne Vetter, a staff member at the
Mathematisches
Forschungsinstitut
Oberwohlfach, noticed that Lorenz Lindelöf's
picture was missing from the pantheon
above. She kindly emailed
me the splendid Lindelöf photo from the Oberwohlfach archives
that you now see here. Thanks, Ivonne!
I regret that unlike Paul Halmos (1916-2006), I never made it a
practice to snap a photo of every mathematician I met.
As a
consequence, I have no photo of Michael Goldberg. If someone
will be kind enough to send me one, I'll be happy to post it.

The Finnish topologist
Ernst Leonard Lindelöf
(1870-1946)
was the son of Lorenz Lindelöf. He was principally a
topologist and complex analyst. Today he is much better
known than his father. (It appears that he never published
anything about the isoperimetric problem for polyhedra.)
Which convex polyhedron with n faces
has the smallest value of the ratio
A 3/V 2?
(A = surface area and V = volume.)
here as IQ. Because it is dimensionless, it is independent of scale.
In 1897, Minkowski proved the existence of a roundest polyhedron
for every n ≥ 4.
In 1899 it was proved by Lorenz Lindelöf that a
necessary condition for a polyhedron
P to be roundest is that
P circumscribes a sphere
tangent to the faces of
P at
their respective centroids.
For a polyhedron circumscribed about the unit sphere,
A/V = 27V = 9A.
Hence minimizing A 3/V 2
is equivalent to
minimizing A (or V).
It has been conjectured — but never proved — that the
roundest
polyhedron is always simple,
i.e., that its vertices are all of degree three.
I learned a little about roundest polyhedra in 1972 when I watched
Klee's
two films about geometry,
'Shapes of the Future — Some Unsolved Problems
in Geometry'. In 1975, Prof. Klee (1925-2007)
gave me copies of the filmscript
booklets for these two films,
Part I: Two Dimensions and
Part II: Three Dimensions.
With the permission of the
Mathematical Association of America,
I have made
digital copies of these films and uploaded them
to YouTube:
Part I: Two Dimensions (YouTube video)
and
Part II: Three Dimensions. (YouTube video)
When I read Klee's booklet for Part II, I found the
"attractive conjecture" he describes
in the next-to-last paragraph of page 5 to be implausible.
(That page is reproduced below.)
I then confirmed by calculation that although Klee's conjecture
does hold for n < 8, it is
false for n = 8, i.e., the polar of Berman and
Hanes' 8-vertex polyhedron
is not tangent
to the unit sphere at face centroids (cf. my scrawled comment at
the bottom of page 5).

Page 5 of Victor Klee's booklet for Part II, which
includes his 'attractive' (but false) conjecture.
Below are stereoscopic images of the polyhedra for
— shown in red — 4 ≤ n ≤ 35

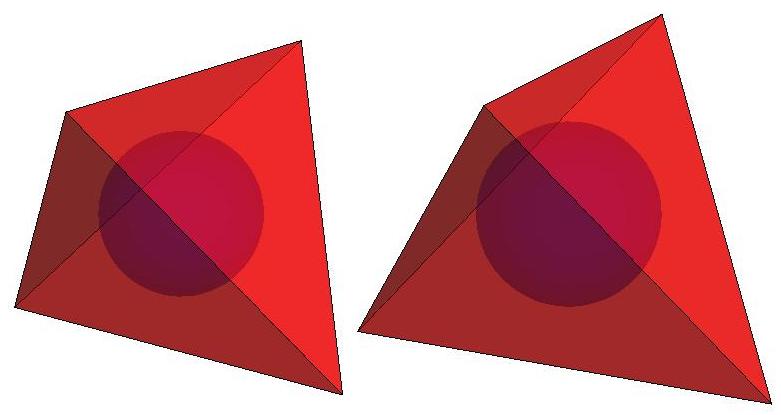
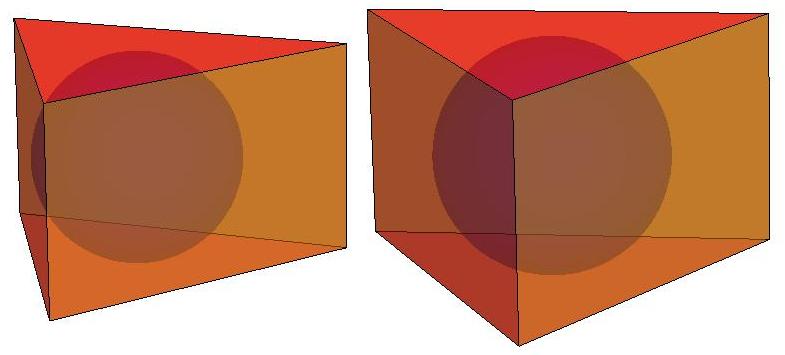
n = 4
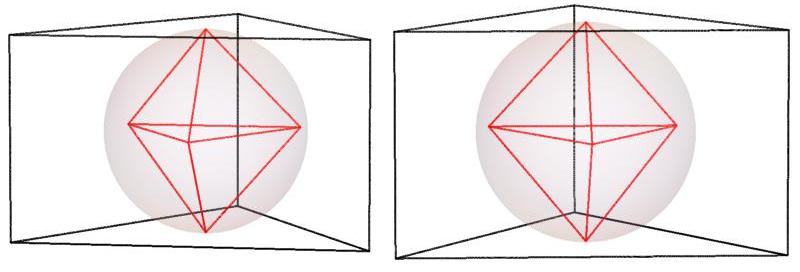
n = 5
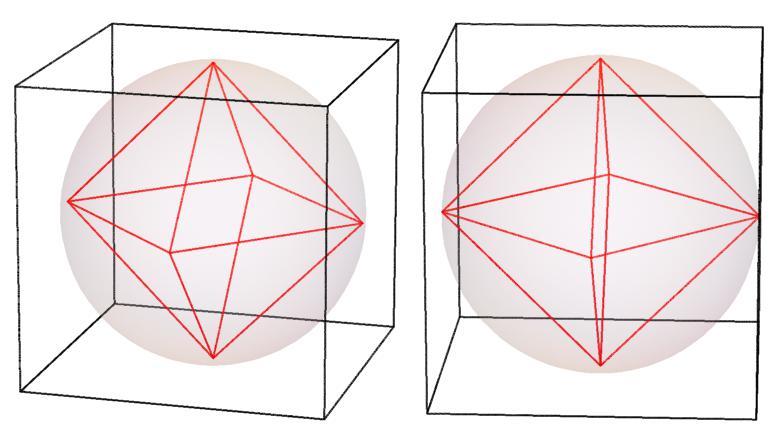
n = 6
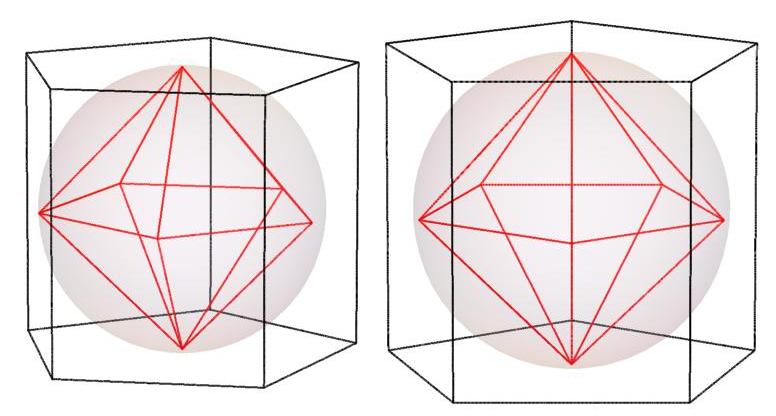
n = 7
n = 8
.jpg)
n = 8
I met Michael Goldberg several times at AMS meetings in the late sixties.
We
discussed minimal surfaces and Voronoi polyhedra, but unfortunately
he never
brought up the subject of roundest polyhedra,
in which I had a growing interest.
Like Victor Klee, Michael was an unusually modest man.
I greatly regret that
he never mentioned to me either of his
groundbreaking publications about polyhedra:
'The Isoperimetric Problem for Polyhedra'
(1934)
and
'A Class of Multisymmetric Polyhedra'
(1937).
In 1985 I discovered Goldberg's 1935 article, but only in 1991,
when I bought
Ian Stewart's wonderfully witty book about mathematics,
"Game, Set, and Math",
did I learn of Michael's 1937 article
introducing what are now
called
Goldberg
polyhedra, a class of polyhedra based on the regular
icosahedron.
Donald Caspar and Aaron Klug independently
rediscovered Goldberg polyhedra
in 1962.
They are related to the structure of several common viruses
and are described
in the Caspar-Klug publication,
"Physical Principles in the Construction of Regular
Viruses",
Cold Spring Harbor Symp. Quant. Biol. 27, pp. 1-24
(cf.
VIRUSWORLD).
My computational geometry 1986 IBM conference paper,
'A Defect-Correction Algorithm for Minimizing the Volume
of a
Simple Polyhedron Which Circumscribes a Sphere',
summarizes my 1986 computer investigation of roundest polyhedra.
Conjectured solutions for 4 ≤ n ≤ 35
and for n = 42 are described and
illustrated. Shortly before the conference, I
issued a
supplement
that includes
conjectured solutions
for 36 ≤ n ≤ 41
and n = 43. (This supplement also
contains
William Tutte's
analysis of the asymptotic number of
simple polyhedra as a function of the number n of faces.)
I made final runs in late 1986 and obtained solutions for n = 45, 46, and 47.
Among the most interesting results of this study were
(a) the discovery of the first example (n = 25) of an
asymmetric polyhedron I conjectured to be roundest;
(b) the discovery of the first example (n = 33) of a
polyhedron— also conjectured to be roundest —
that contains a heptagon.
(c) additional data that support a discovery I made in 1975,
proving the falsity of a conjecture of Victor Klee.
Klee conjectured that for every n>=4, Qn,
the roundest
polyhedron, and Pn, the polyhedron of maximum volume
among all polyhedra with n vertices inscribed in the sphere, are
what I will call strictly dual, i.e. that the
vertices of Pn
coincide with the face centroids of Qn.
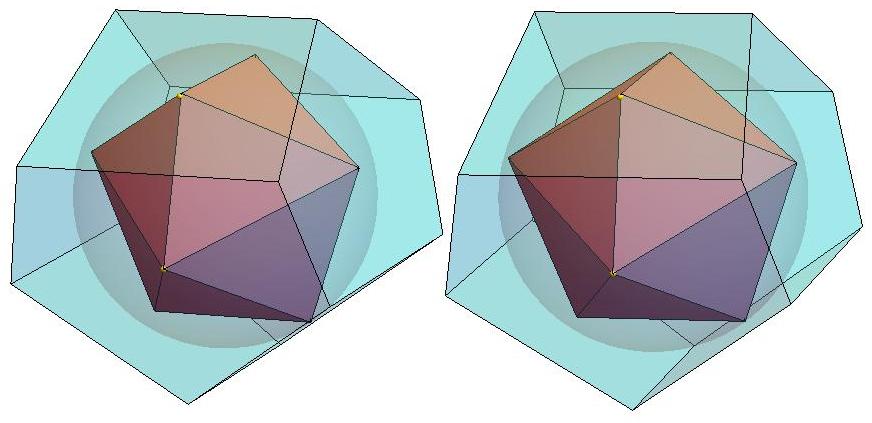
Schlegel diagram
Convex hull
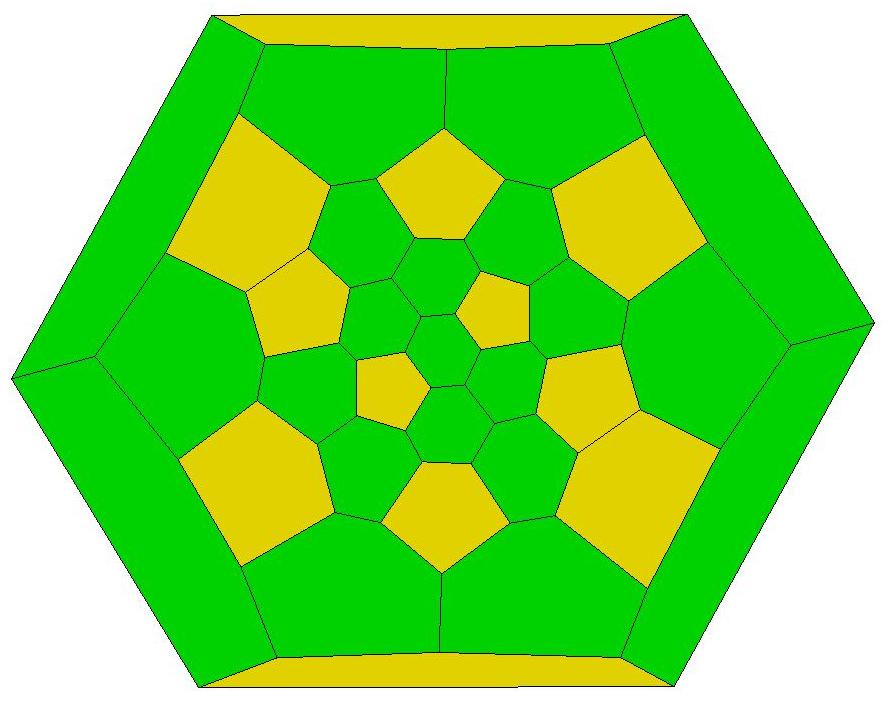
Neil Sloane's Q9, the arrangement of nine points on the unit
sphere S for which the convex hull has maximum volume.
.jpg)
Schlegel diagram
Convex hull
The polyhedron P9, which is found to have minimum volume
among all 9-faced polyhedra that circumscribe the unit sphere S

Edge skeleton of the inscribed polyhedron Q9

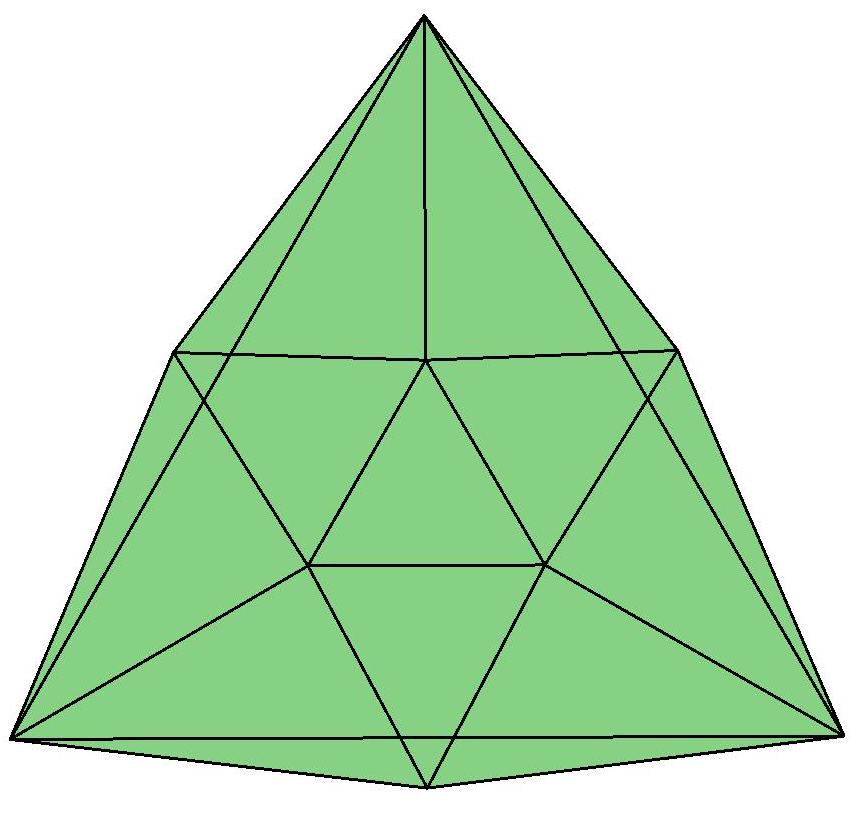
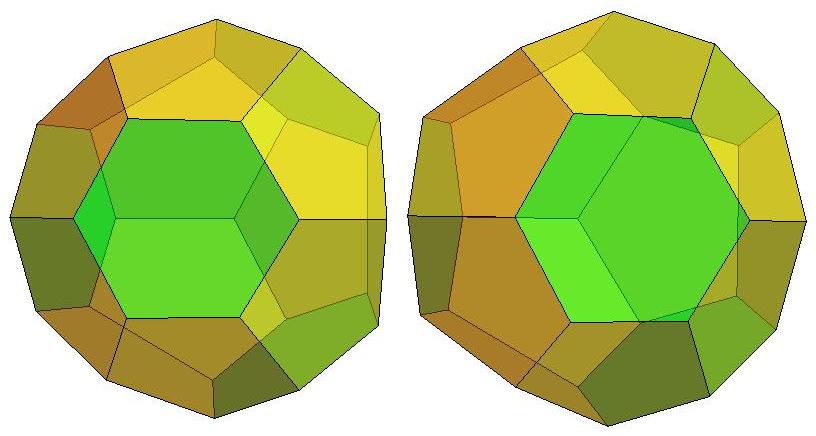
Edge skeleton of Q122, a simplicial polyhedron with
122 vertices, 362 edges, and 240 faces. Q122 has full
icosahedral symmetry. (Discovered by Neil Sloane et al)
Q122 is found to have the largest volume among
polyhedra with 122 vertices
that are inscribed
in the unit sphere. It is the topological dual of a
Goldberg polyhedron P122 that in 2015 was
found by Wayne Deeter to have the smallest
volume among polyhedra with 122 faces that
are circumscribed about the unit sphere.
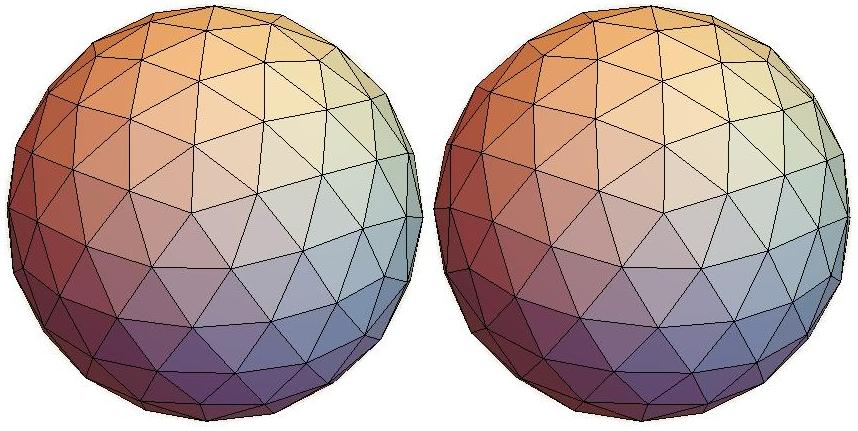
The inscribed polyhedron Q122 (a Goldberg polyhedron)

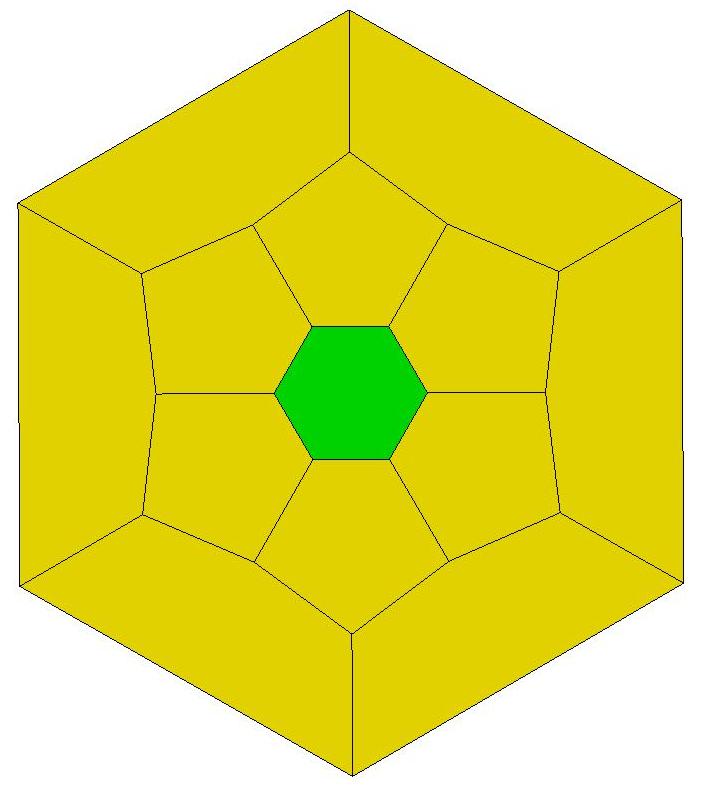
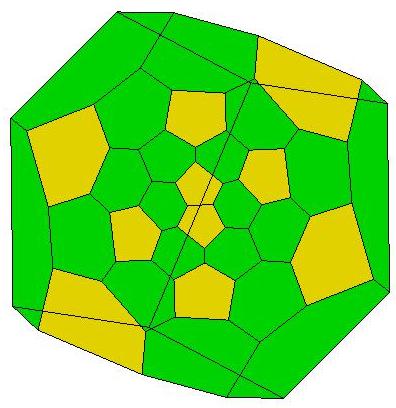
Pied tiling of Q122
It has 240 triangle faces: 60 yellow, 120 green, and 60 red.
The ratios of the triangle areas are [approximately]
yellow : green : red = 1 : 1.125 : 1.148.

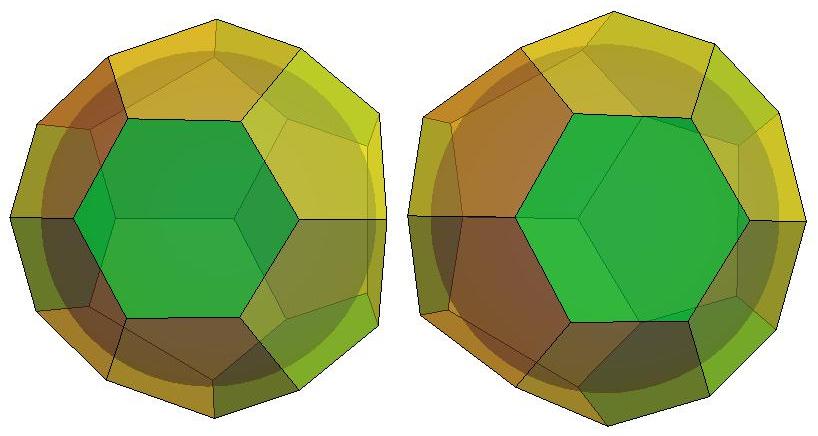
Q122 — nested rings (axial view)

Q122 — nested rings (oblique view)
Schlegel diagram of Q122
.jpg)
Schlegel diagram of the circumscribed polyhedron P122
Schlegel diagram of the circumscribed polyhedron P122

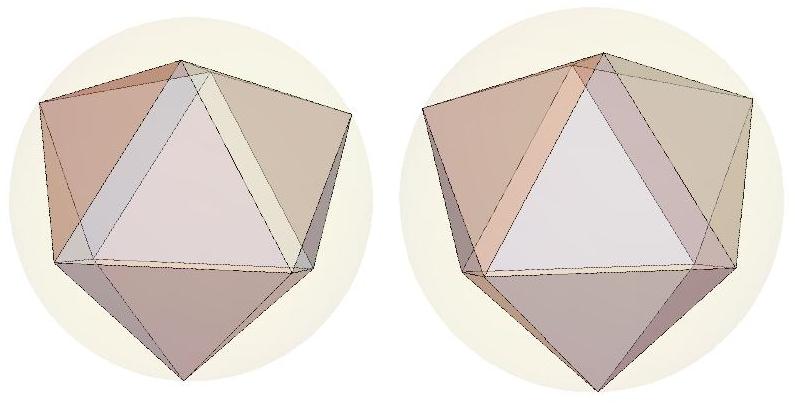
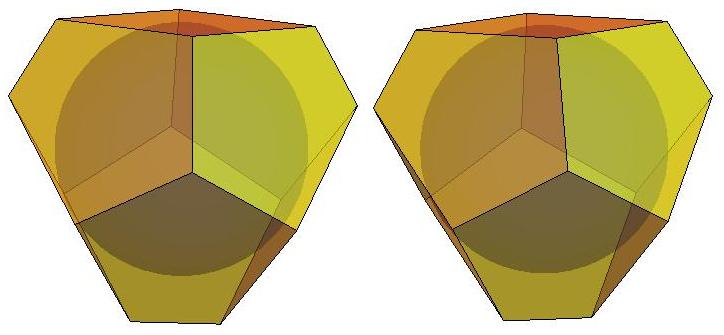
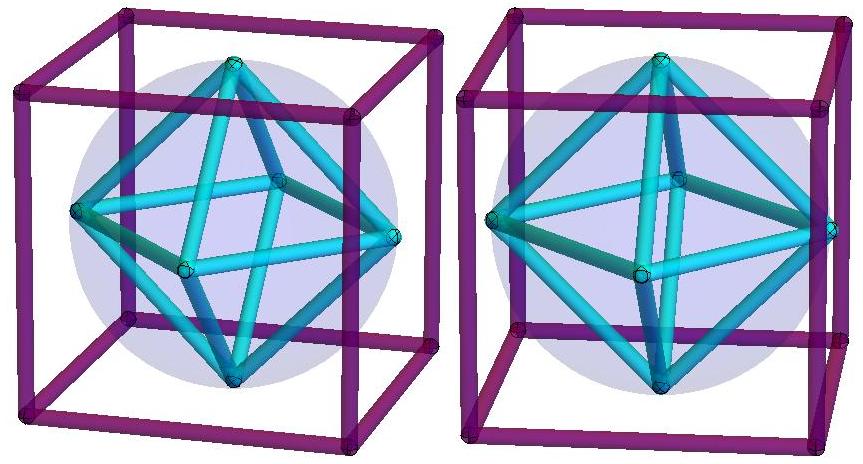
The blue polyhedron P8, which has
eight faces,
is shown here circumscribed about the unit
sphere.
A second polyhedron Q8, which has
eight vertices,
is shown inscribed in the same
sphere. In 1967, Joel Berman and Kit Hanes proved that
Q8
has the largest volume among
polyhedra with eight vertices inscribed in the unit sphere, and
they derived exact expressions
for its vertex coordinates.
In 1934, Michael Goldberg conjectured that P8
has the smallest
volume among polyhedra with eight faces that circumscribe the unit
sphere, but no analytic
expressions are known for its coordinates.
When the two polyhedra are oriented so that the
axes of rotational symmetry and planes of reflection symmetry of
P8 coincide with those
of Q8,
the face centroids of P8
are almost coincident with the vertices of
Q8. The gap
between the face centroids of P8
and the vertices of Q8 is equal to ~0.04700640080523555
on each quadrilateral face
and ~0.003249596513702373 on each pentagonal face.
Tiny yellow
dots mark the centroid locations on one pentagonal face and
on one quadrilateral face.
In the spring of 2015, I was happily surprised to
receive an email from Wayne Deeter, who
informed me that he too had been investigating
roundest polyhedra. He had accumulated an
enormous body of results, which he generously sent me,
from runs of an optimizing computer
program of his own
that he only later discovered is based on an algorithm
very similar to
the one I designed for 'Lindelöf', the optimizing
program I wrote in FORTRAN in 1986.
Lindelöf begins by generating
an n-faced polyhedron circumscribed about the unit sphere.
The
points on the sphere where
the face planes are initially tangent are randomly distributed, but
in every iteration, the faces are appropriately
tilted, causing
their tangent points to migrate on the
sphere in such directions that the gaps between the face
centroids and their tangent points are reduced.
Eventually
the face centroids and tangent points
coincide nearly exactly.
For each value of n, I
anointed the polyhedron with the smallest area (or
volume) as the roundest one, but since I
was using a statistical sampling method to generate
these polyhedra, my conclusions were
only as good as the statistics would allow.
The dramatic
increase in computer speed that had
occurred during the 29 years after my
1986 study allowed Wayne to make hundreds or
thousands of times more runs than I made
in the interval (4 ≤ n ≤ 47) covered by my study.
It is hardly surprising, therefore, that
for one value of n, 38,
Wayne discovered a very slightly
rounder polyhedron than the one I had conjectured was roundest.
Wayne has enormously expanded
the scope of this field by examining polyhedra with far more
faces than any I considered in 1986. This great expansion has enabled him to draw
conclusions
regarding many aspects of the problem that — for the first time —
have good statistical support.
In late 1986,
my polyhedra research notebooks were accidentally lost while the
contents of my
office were being moved to another building across campus,
and they were never recovered.
I then decided
to discontinue my computer studies of this problem.
But Wayne has generously
allowed me to use his data to reconstruct both graphic images
and physical models of the solution
polyhedra I found in 1986 for 4 ≤ n ≤ 47.
Wayne will soon publish an article summarizing his results.
The 19th century German geometer Victor Schlegel introduced the use of flat drawings, which are now called
Schlegel diagrams, to represent the combinatorial structure of convex polyhdra. The geometry of such a
projection diagram is illustrated below for the cube. Let us assume that the faces of the cube are opaque
squares but that the face F has been removed so as to provide a peep hole for a [virtual] observer. The station
point is chosen to be so close to F that the interior surface of every cube face except for F itself is visible.
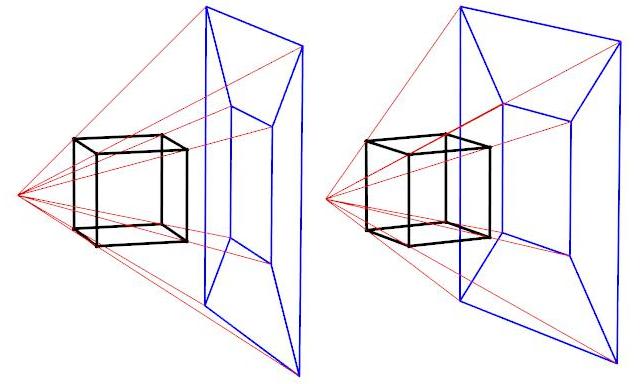
Projection scheme for Schlegel diagram of the cube
.jpg)
Schlegel diagram of the cube
The observer could of course choose instead to locate the station point
just outside a particular vertex V
or an edge E. Schlegel diagrams for the cube under these two arrangements are
illlustrated below.
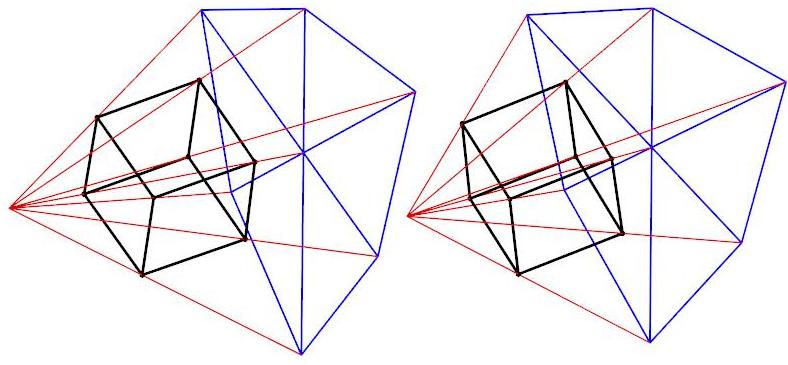
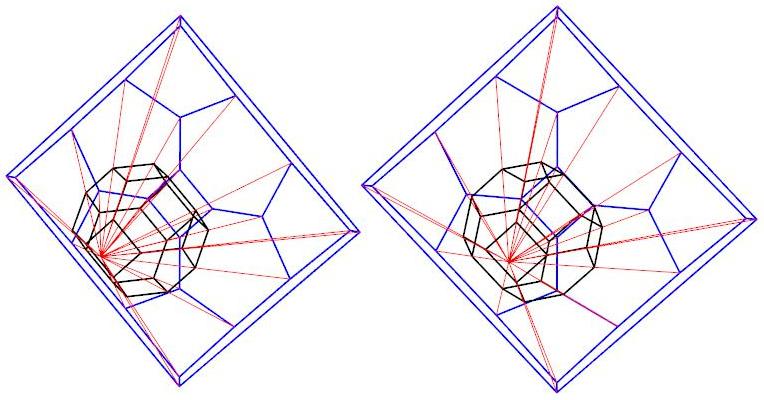
Projection scheme for Schlegel diagram of the truncated octahedron
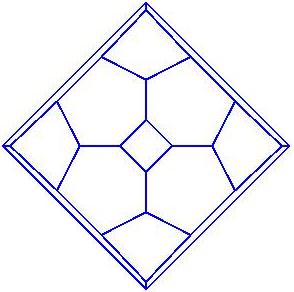
Schlegel diagram of the truncated octahedron
SCHLEGEL DIAGRAMS of conjectured roundest n-faced polyhedra (4 ≤ n ≤ 47)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
4
5
6
7
8
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
9
10
11
12
13
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
14
15
16
17
18
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
19
20
21
22
23
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
24
25
26
27
28
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
29
30
31
32
33
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
34
35
36
37
38
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
39
40
41
42
43
.jpg)
.jpg)
.jpg)
.jpg)
44
45
46
47


4, 5, 6, 7
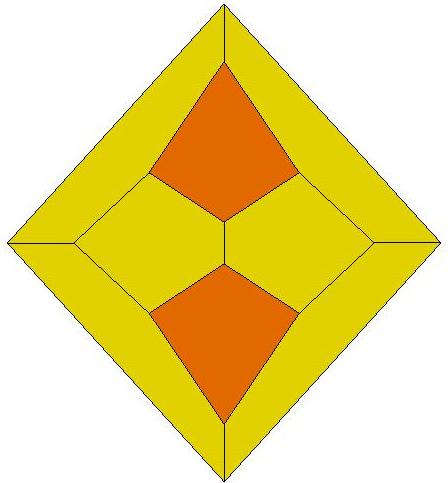
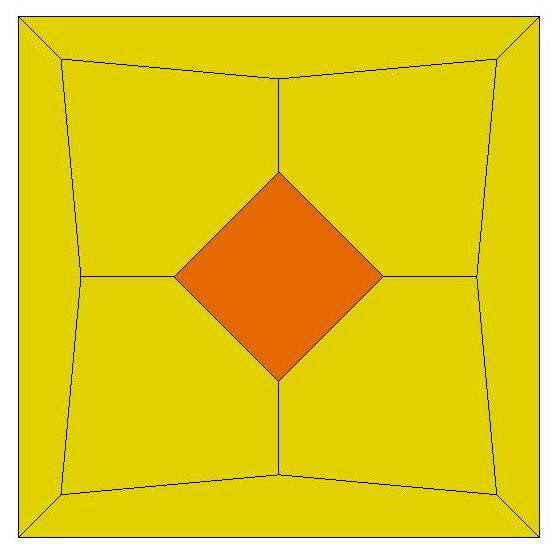
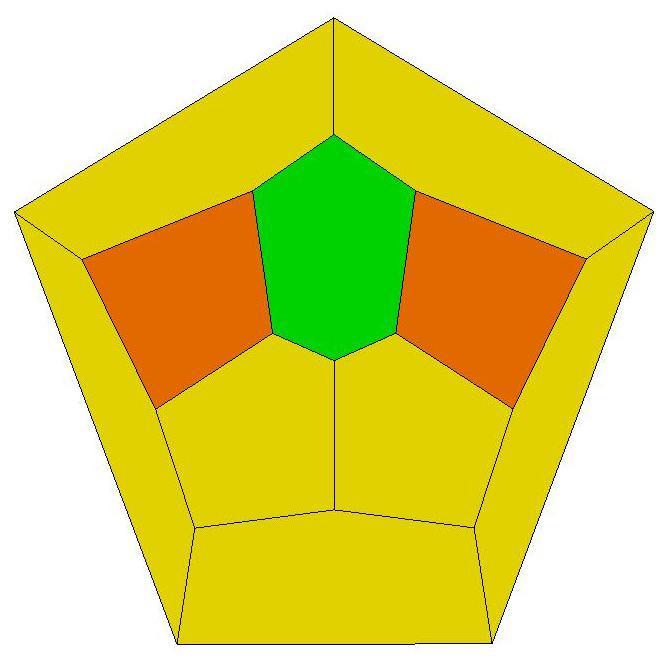
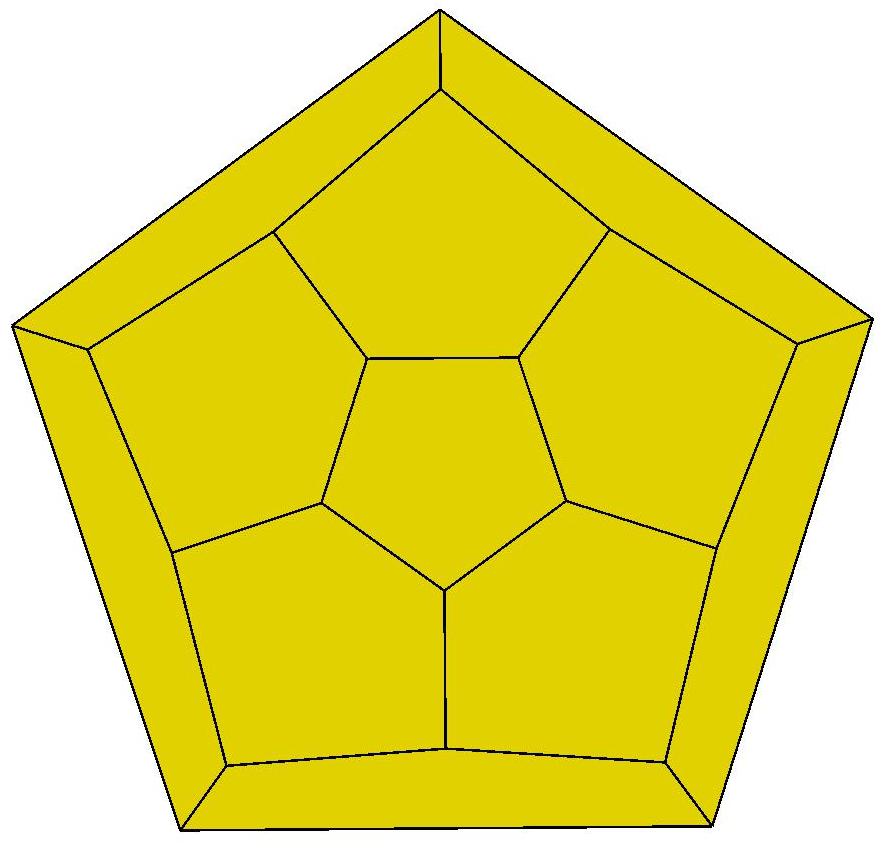
8, 9, 10, 11, 12
.jpg)
.jpg)
.jpg)
.jpg)
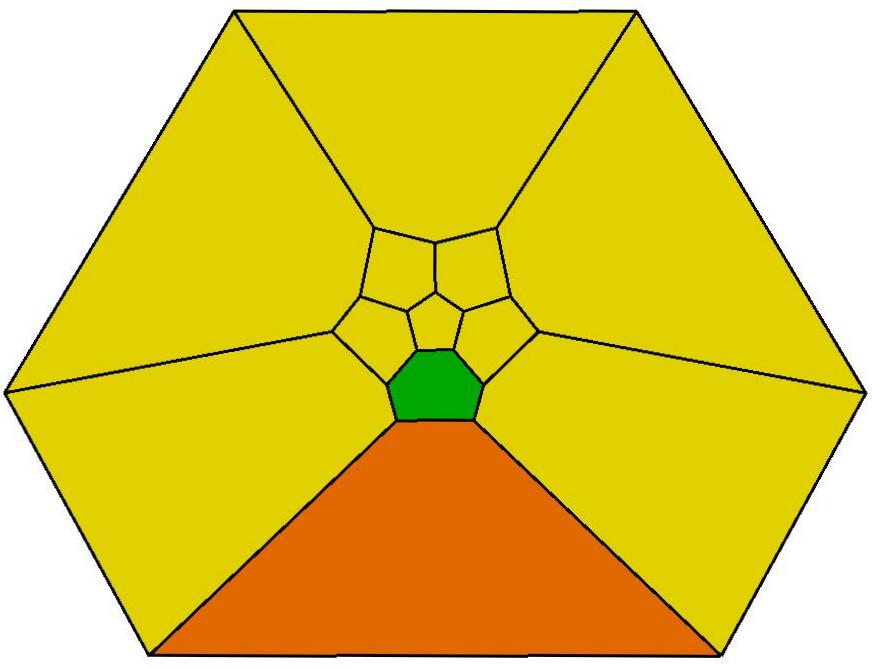
13, 13, 14, 15, 15
.jpg)
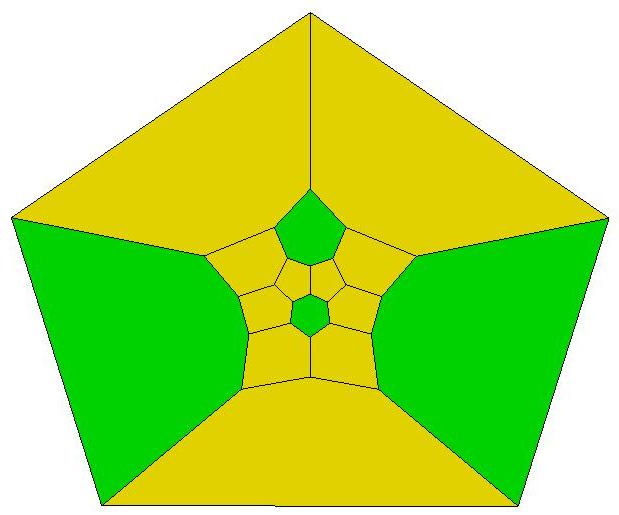
.jpg)
16, 16, 16, 16
.jpg)
.jpg)
.jpg)
.jpg)
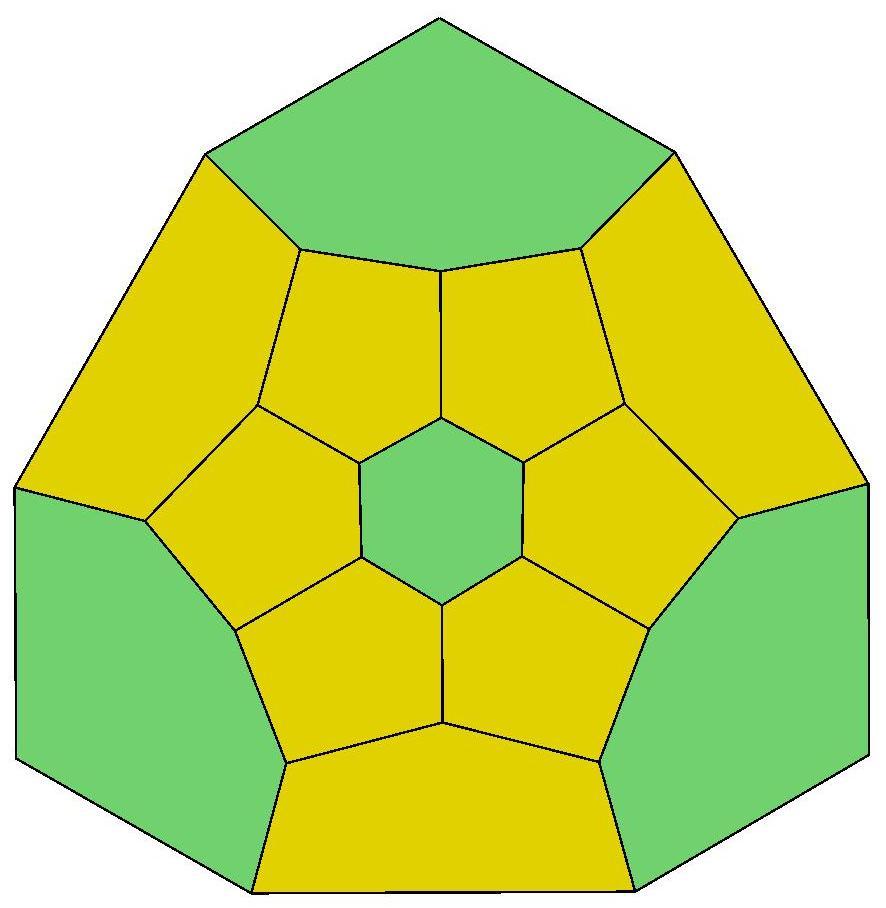
17, 17, 17, 18
.jpg)
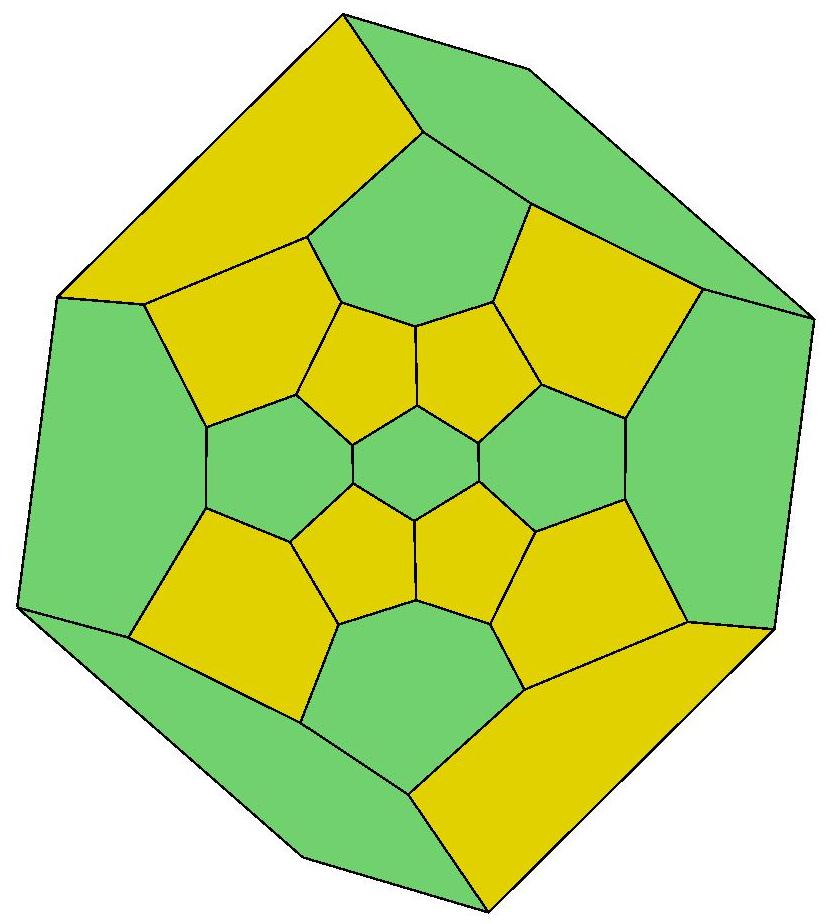
.jpg)
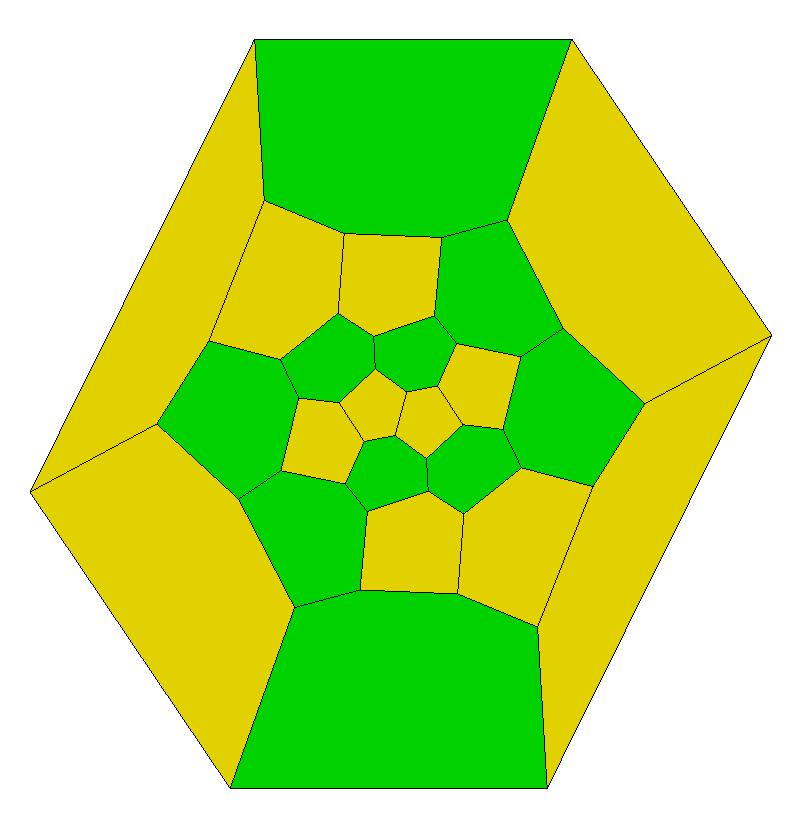
19, 20, 21, 22, 23
.jpg)
.jpg)
.jpg)
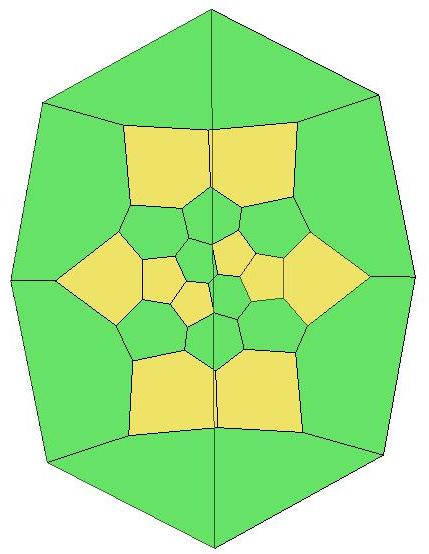
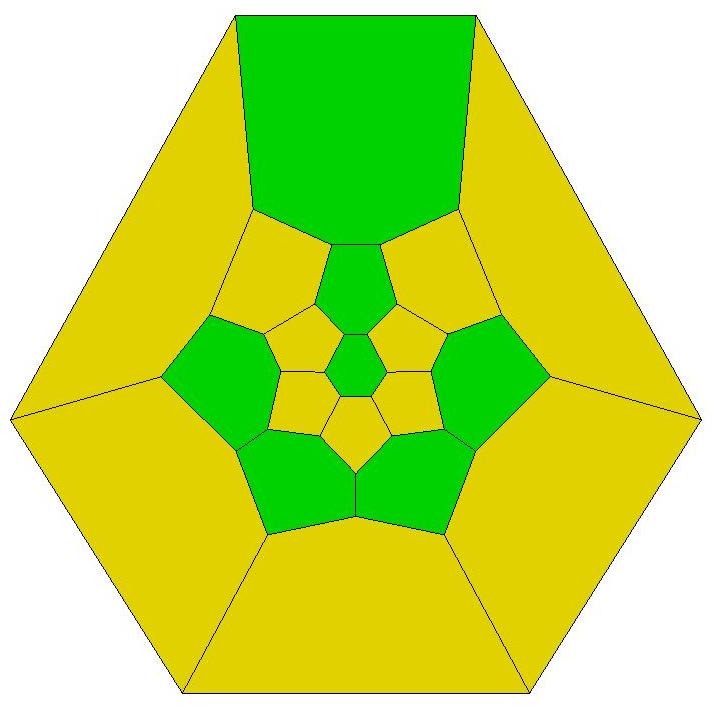
24, 25, 26, 26
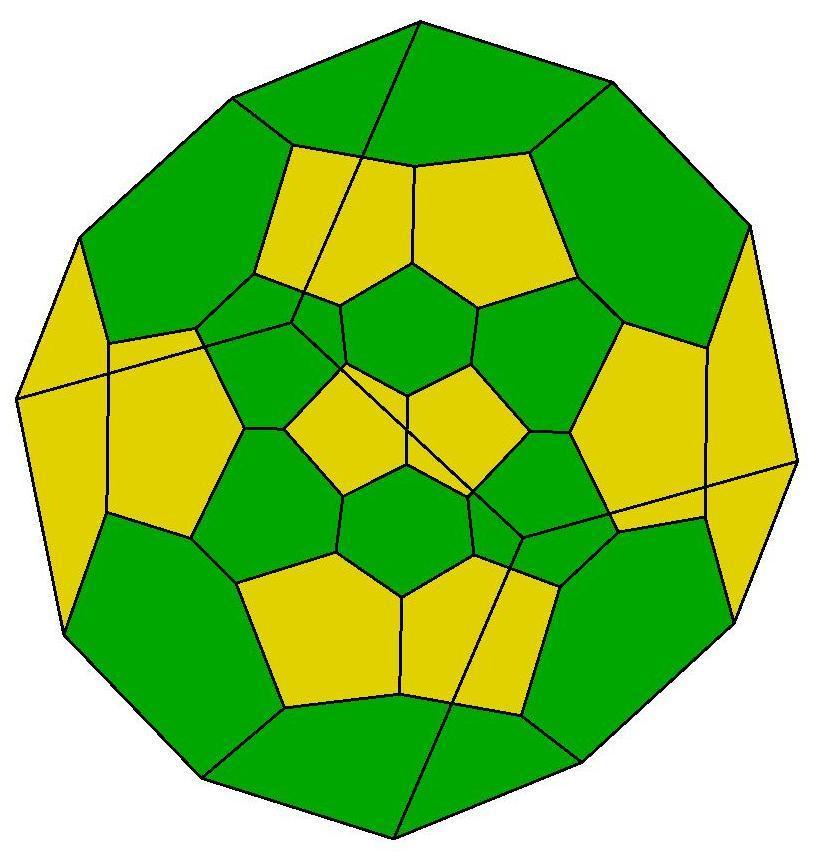
.jpg)
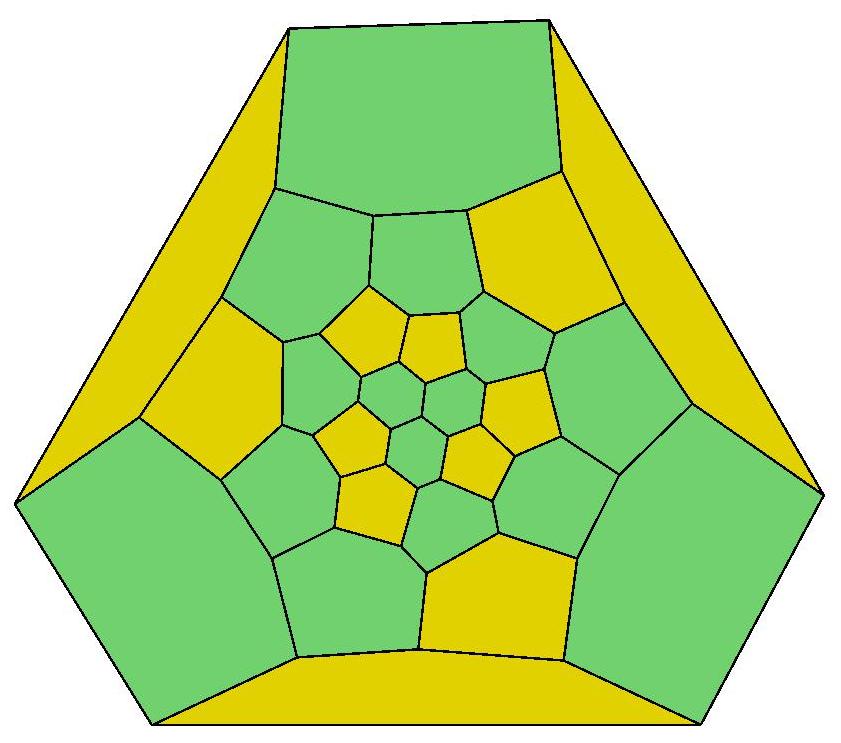
.jpg)
.jpg)
26, 27, 28, 29, 29
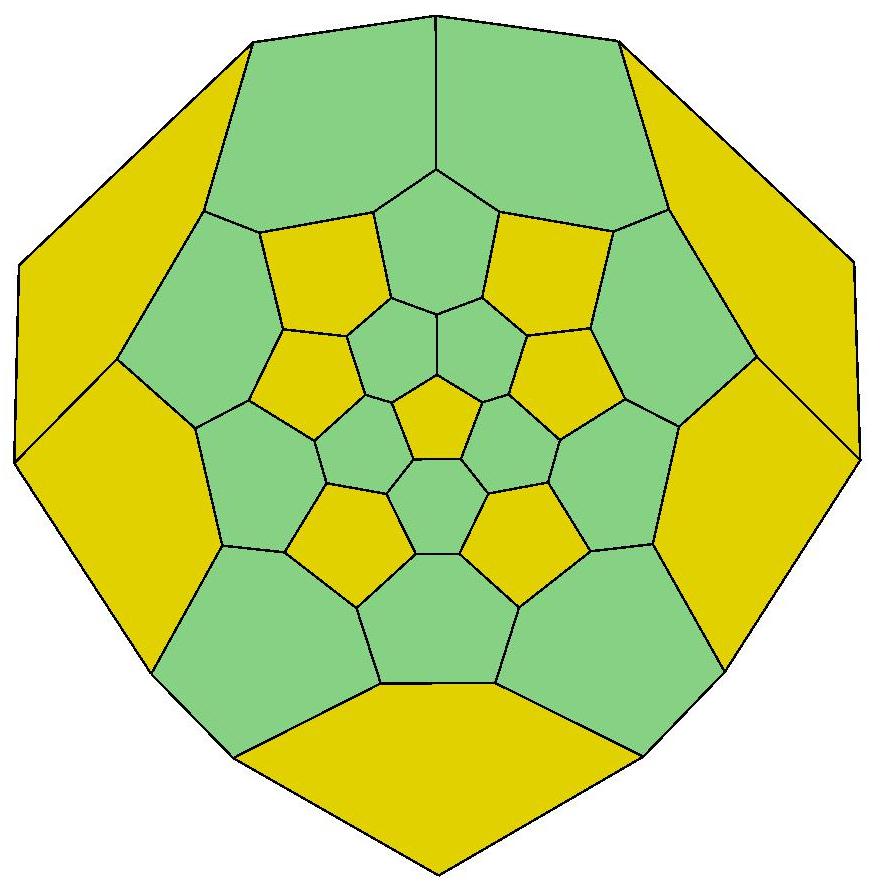
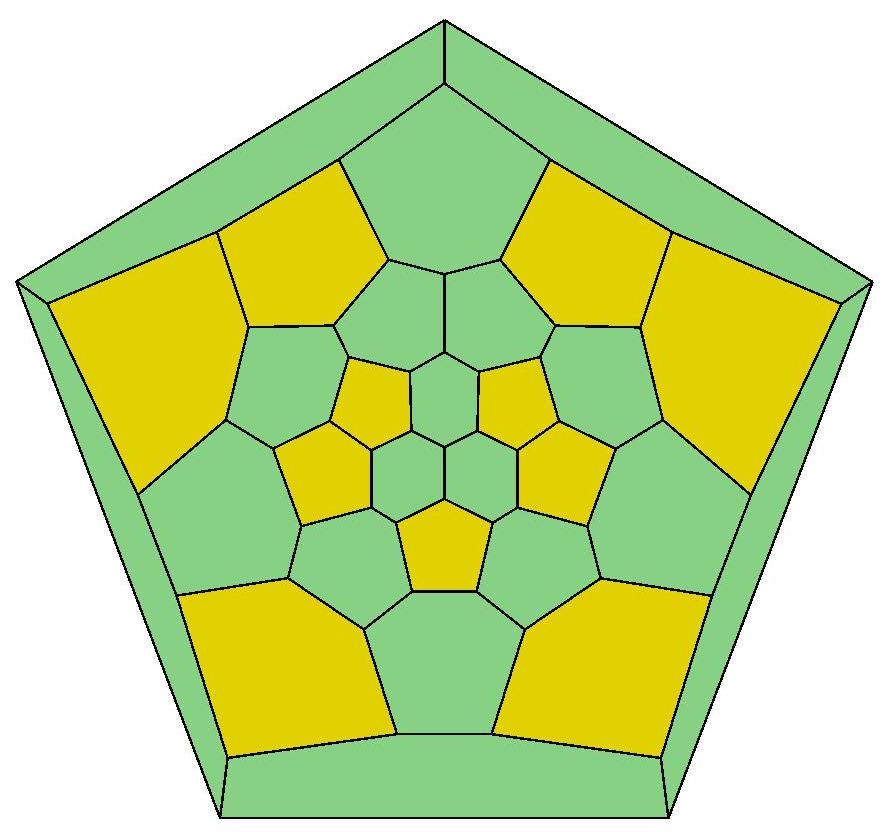
.jpg)
.jpg)
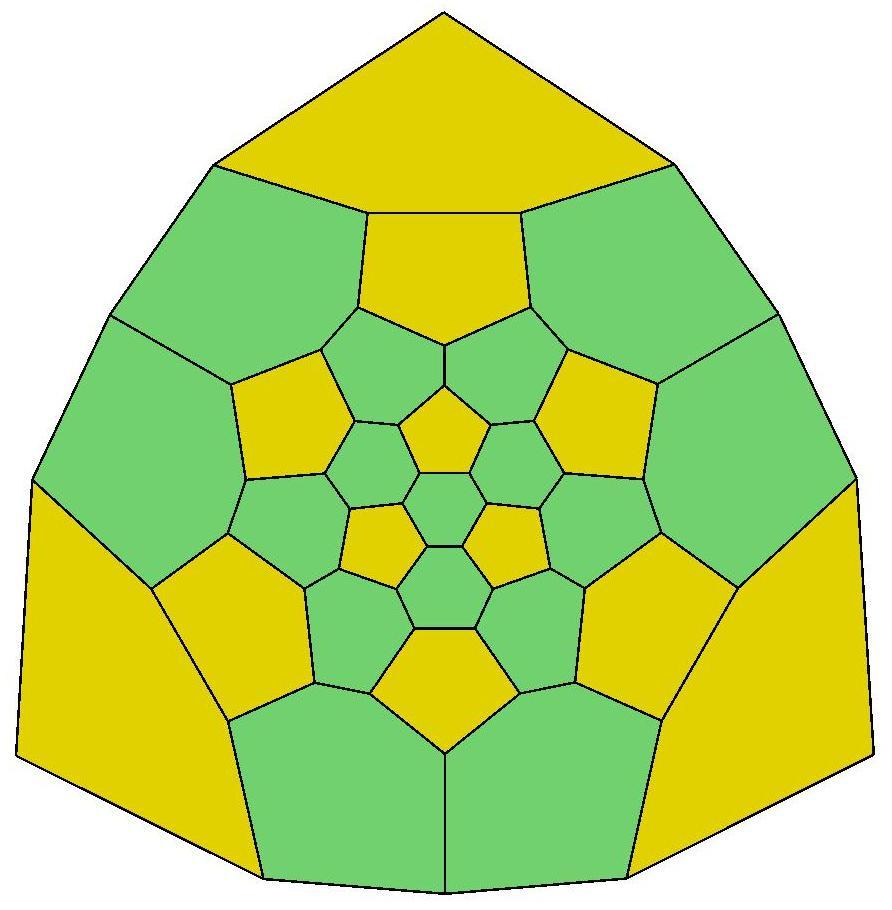
30, 30, 30, 30, 31
.jpg)
.jpg)
.jpg)
.jpg)
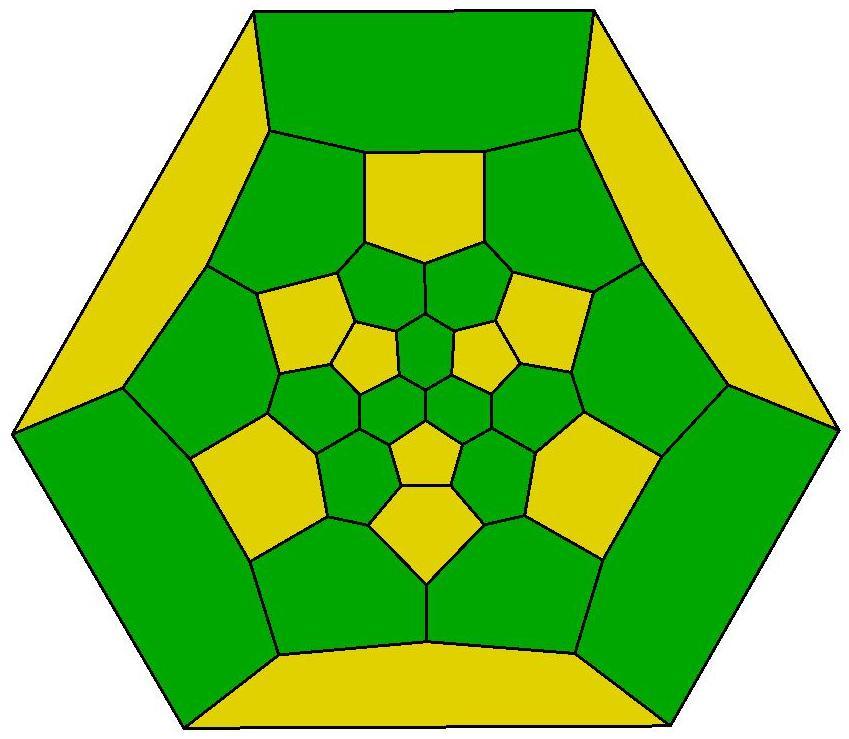
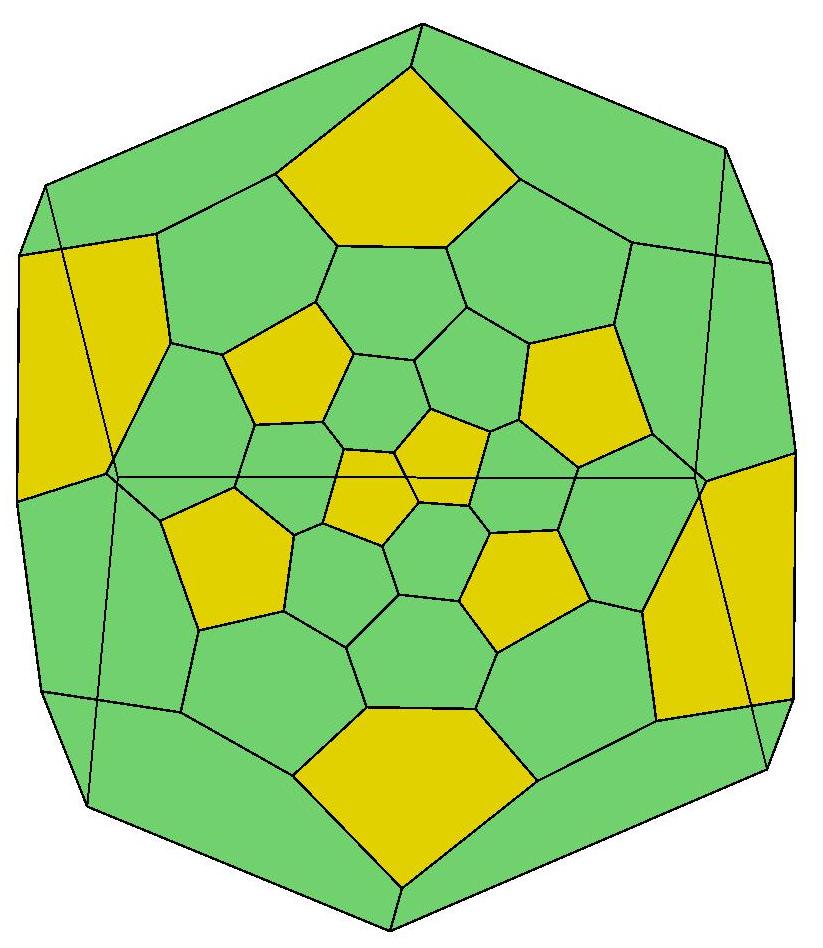
31, 31, 32, 33, 33

.jpg)
.jpg)
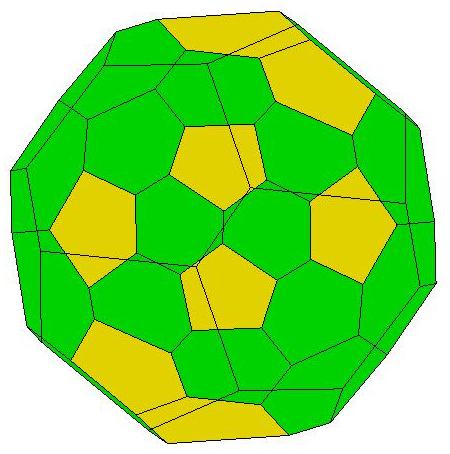
34, 34, 34, 34, 35
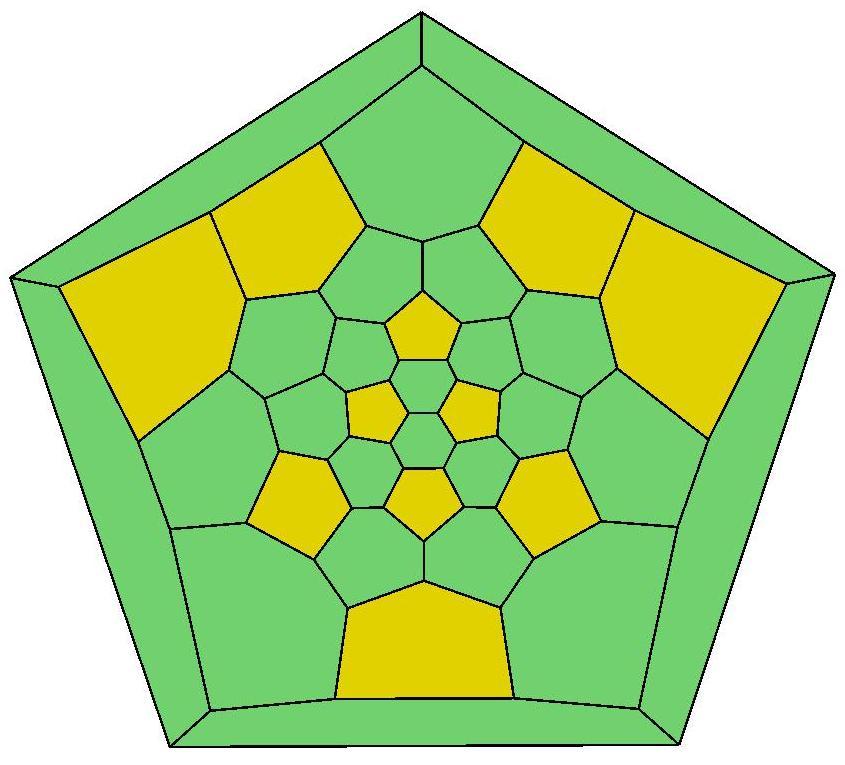
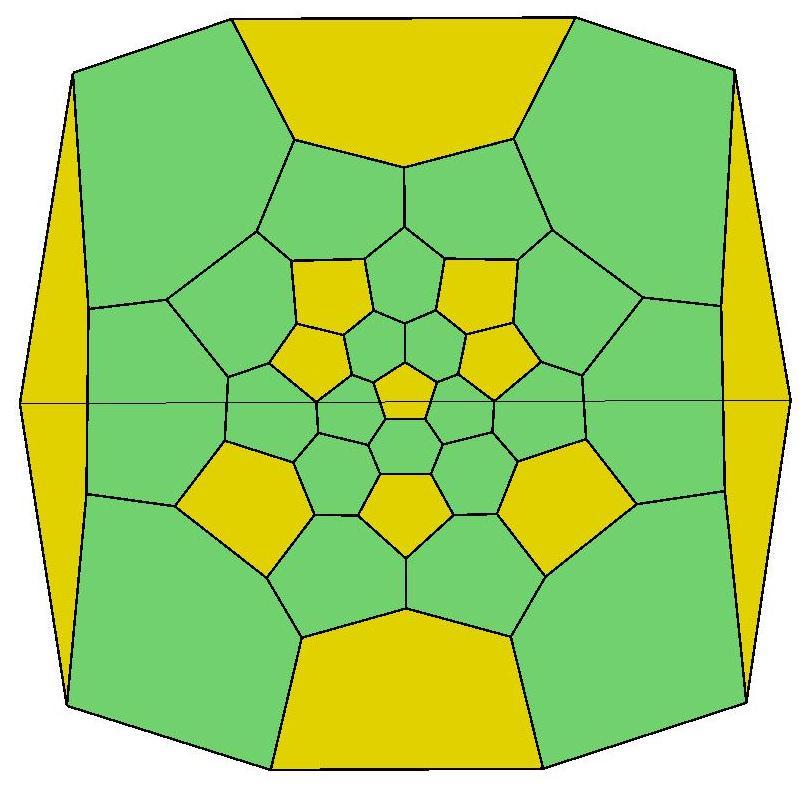
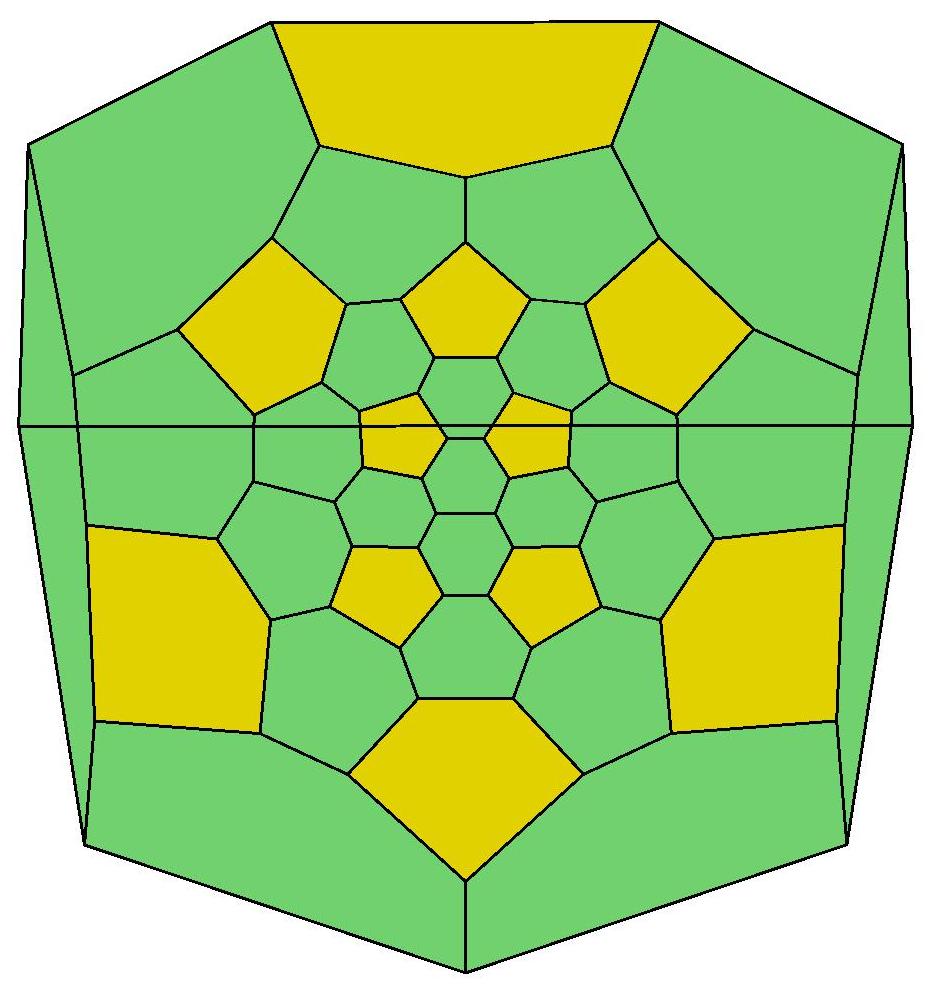
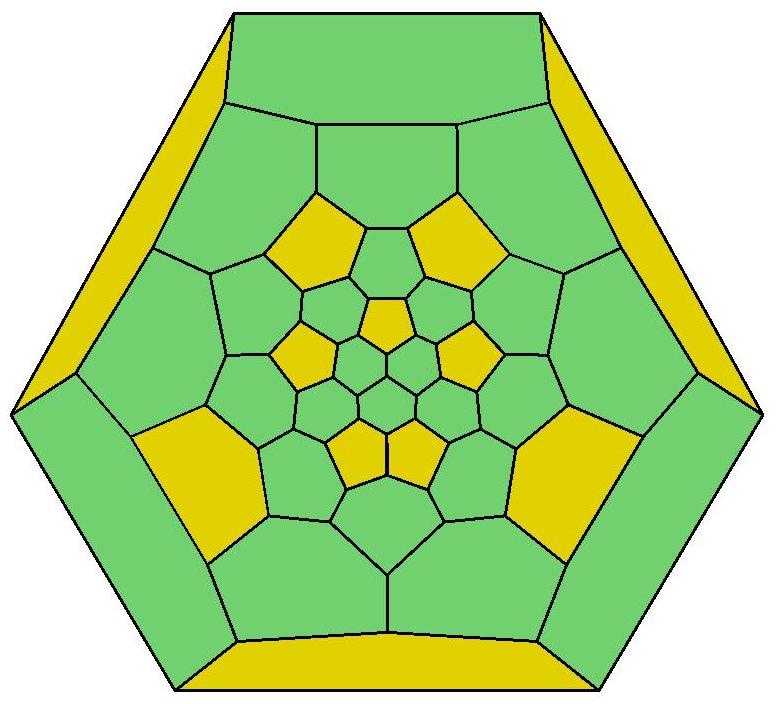
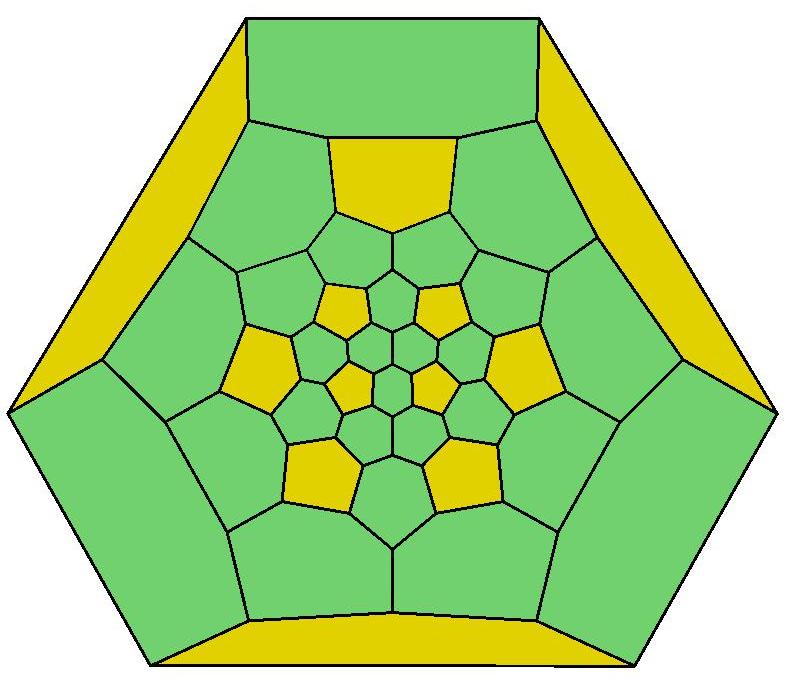
36, 36, 37, 38, 39
.jpg)
.jpg)
.jpg)
.jpg)
40, 40, 40, 41, 42
.jpg)
.jpg)
.jpg)
.jpg)
43, 43, 44, 44, 44
.jpg)
45, 46, 46, 47
Below are schlegel diagrams for the 25 faces of the asymmetrical polyhedron P25:
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
1, 2, 3, 4, 5
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
6, 7, 8, 9, 10
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
11, 12, 13, 14, 15
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
16, 17, 18, 19, 20
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
21, 22, 23, 24, 25
And here are Schlegel diagrams for the 43 faces of P43:
1-5
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
6-10
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
11-15
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
16-20
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
21-25
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
26-30
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
31-35
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
36-40
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
41-43
.jpg)
.jpg)
.jpg)
SCHLEGEL DIAGRAMS AND STEREOSCOPIC IMAGES
OF CONJECTURED ROUNDEST POLYHEDRA FOR
4 ≤ n ≤ 47
(For n = 5, 6, and 7, the sphere-inscribed polyhedra
of maximum volume are also shown for comparison.)

n=4
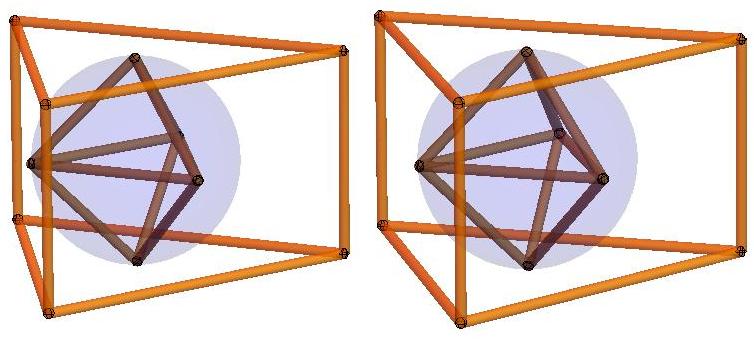
n=5

n=6
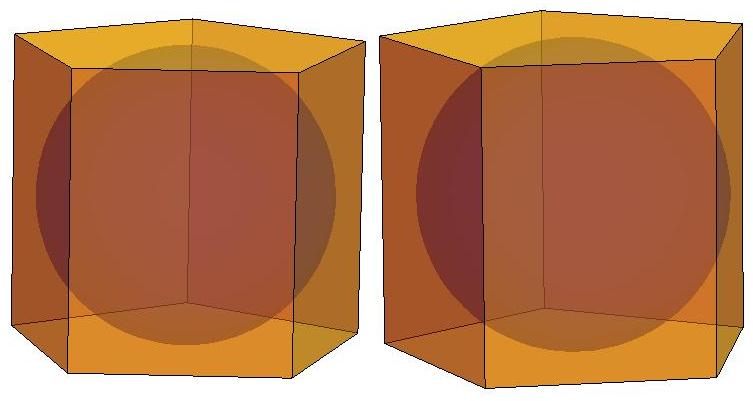
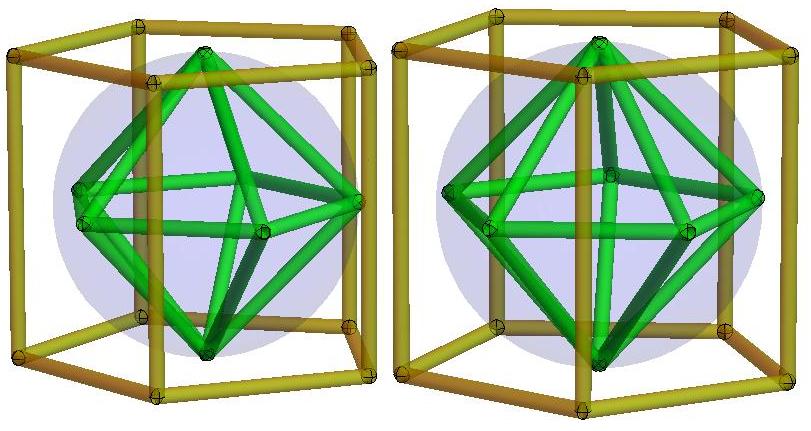
n=7
n=8
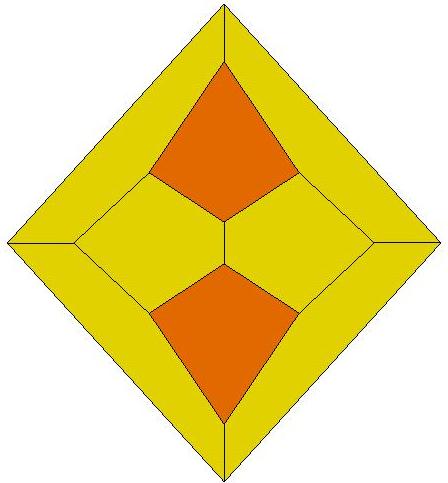
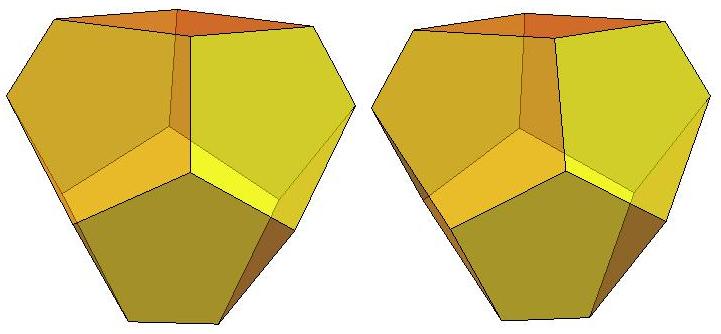

n=9
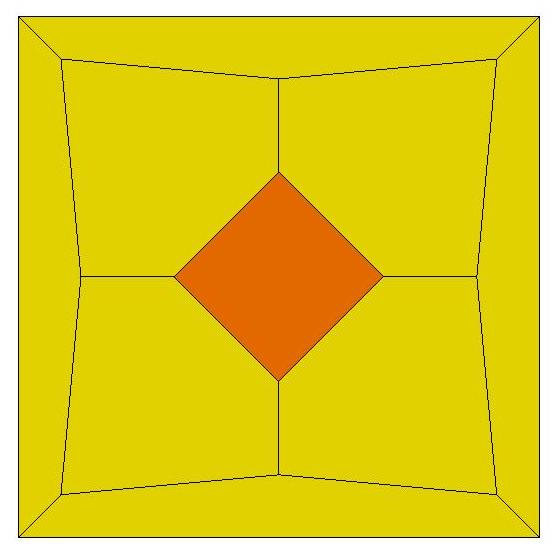
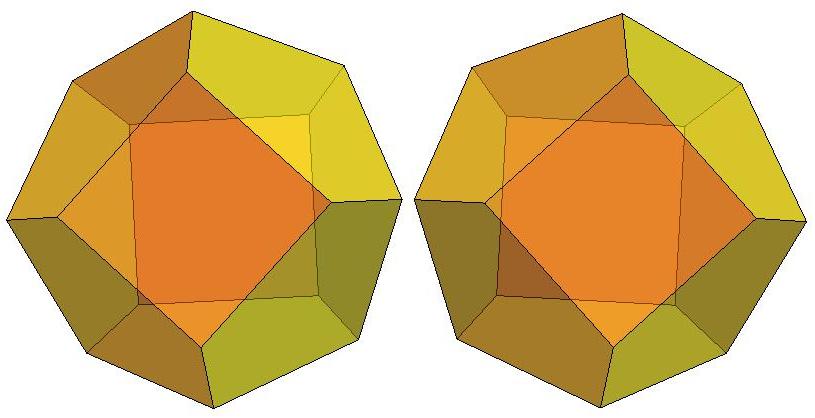
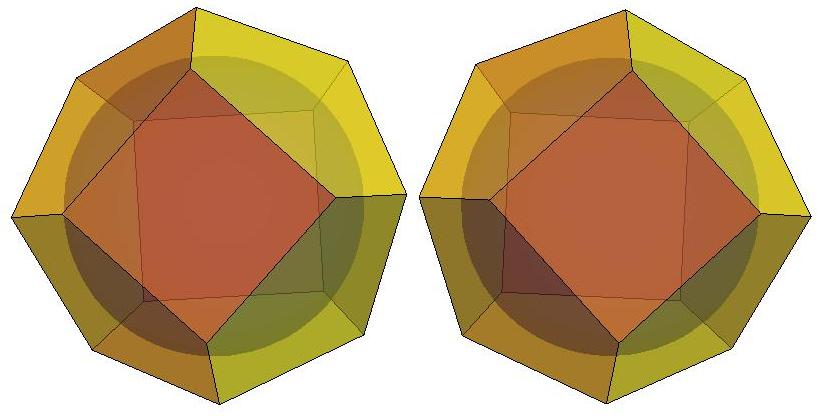
n=10
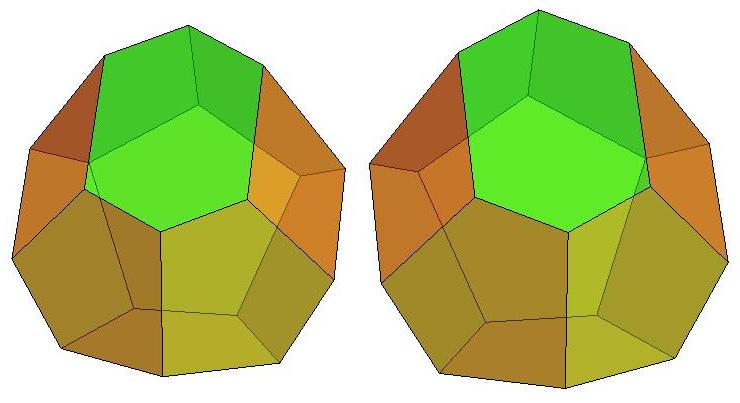
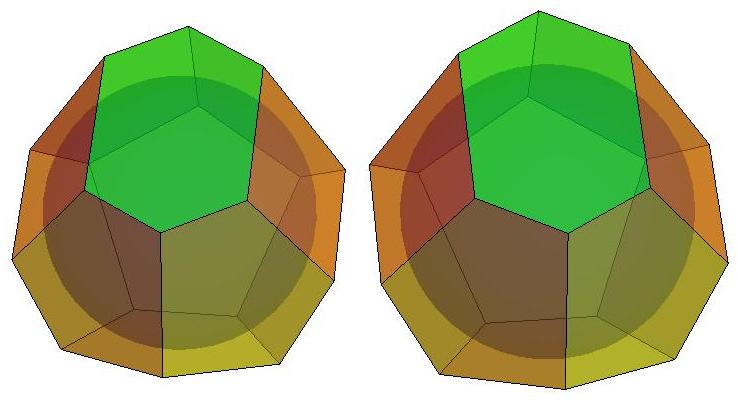
n=11
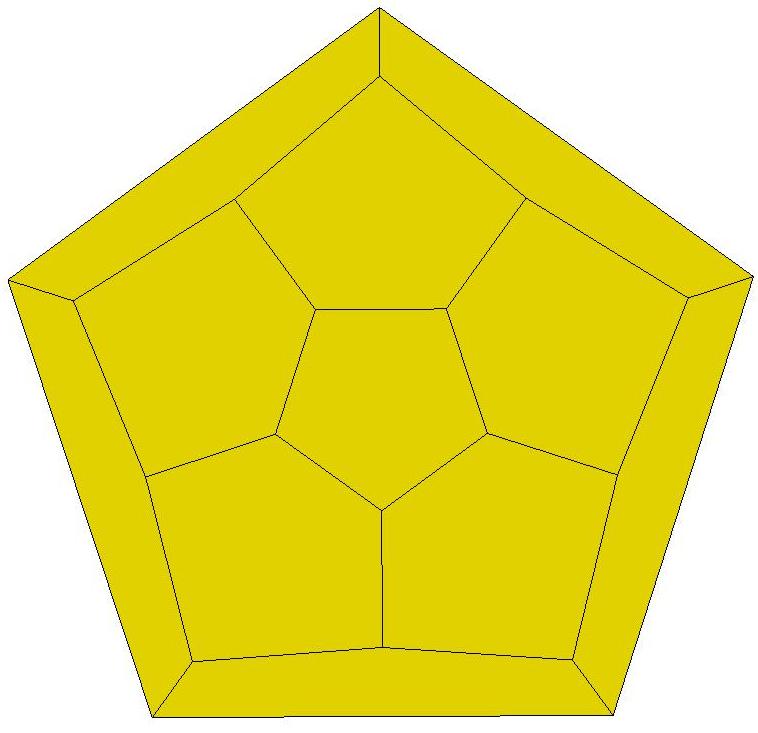
n=12
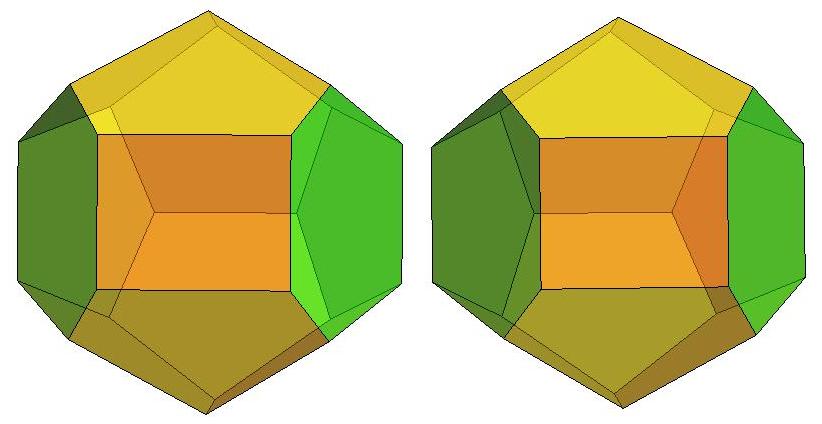
n=13
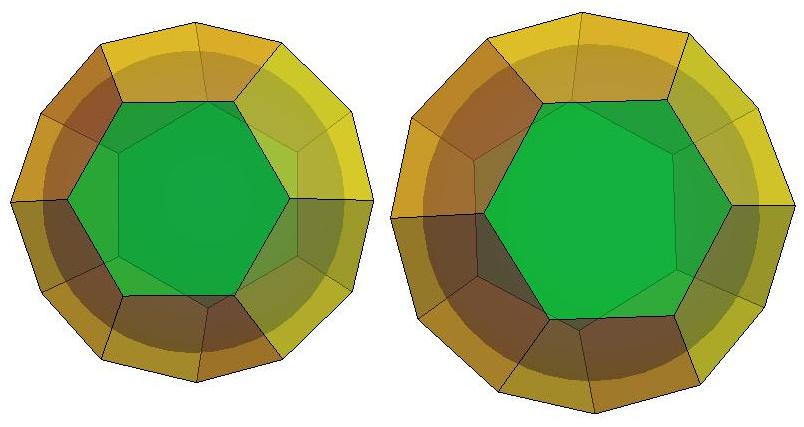
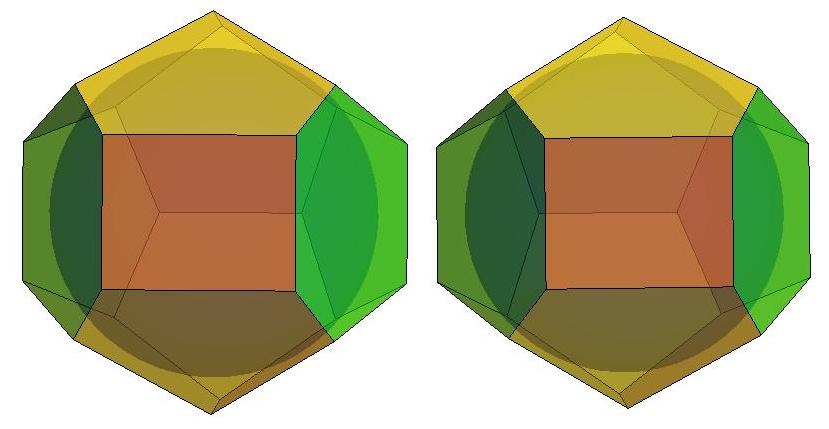
n=14
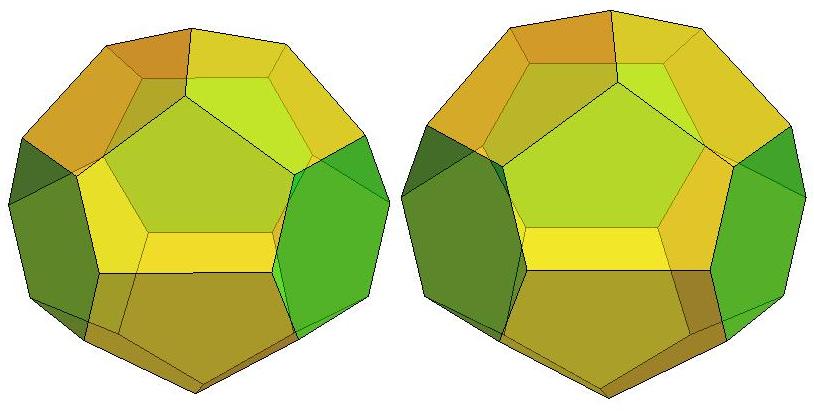
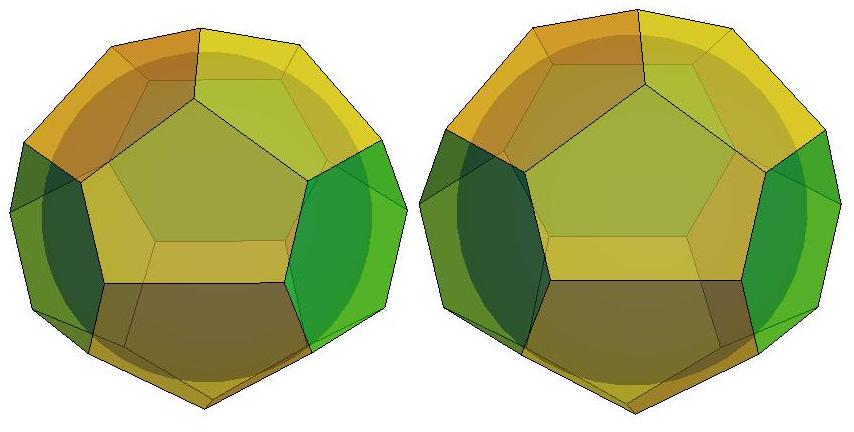
n=15
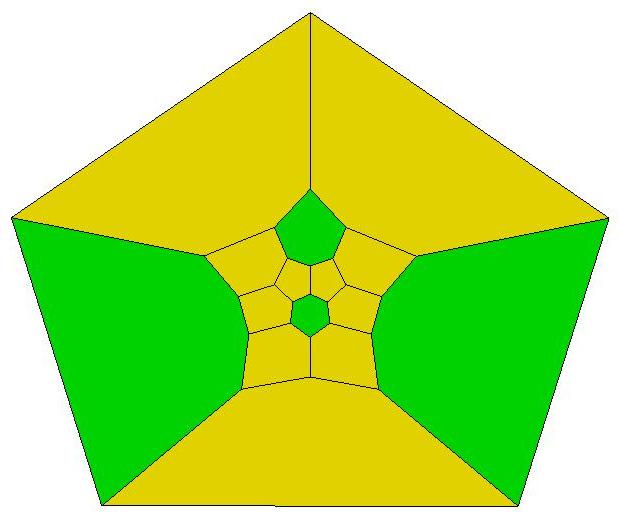
n=16
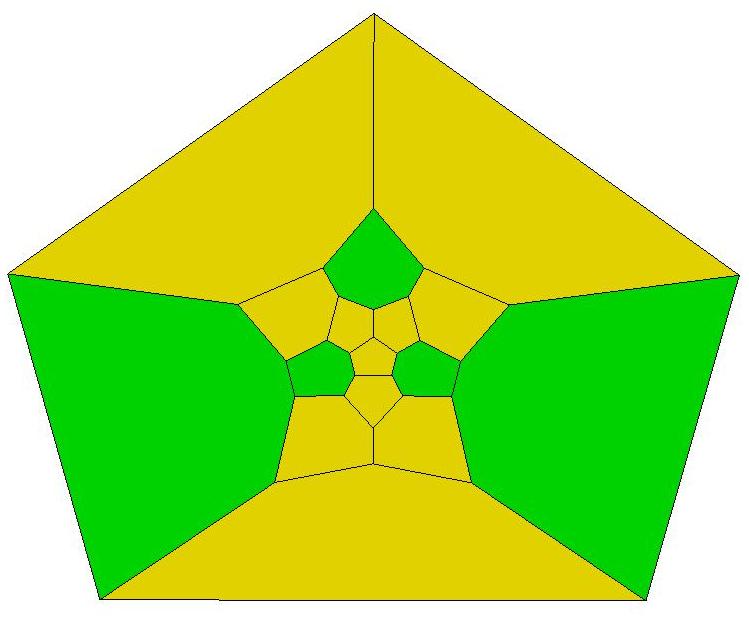
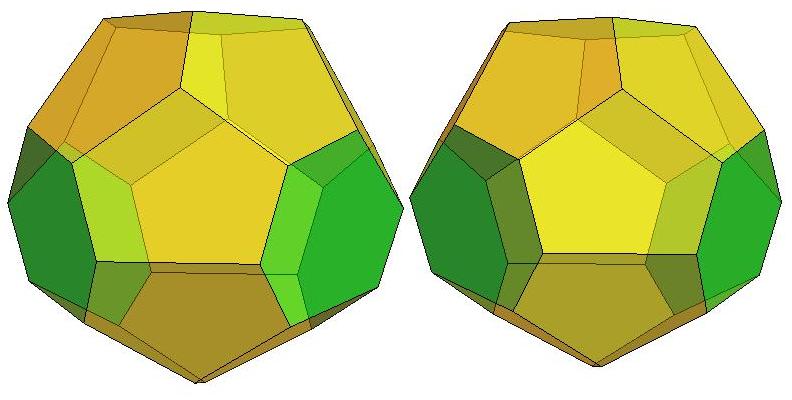
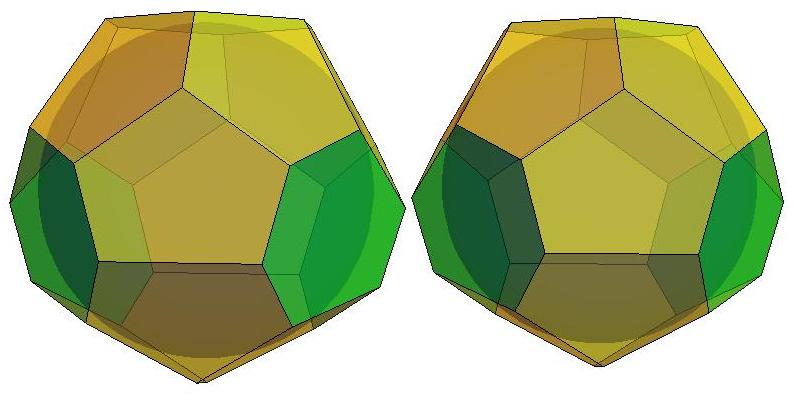
n=17
.jpg)
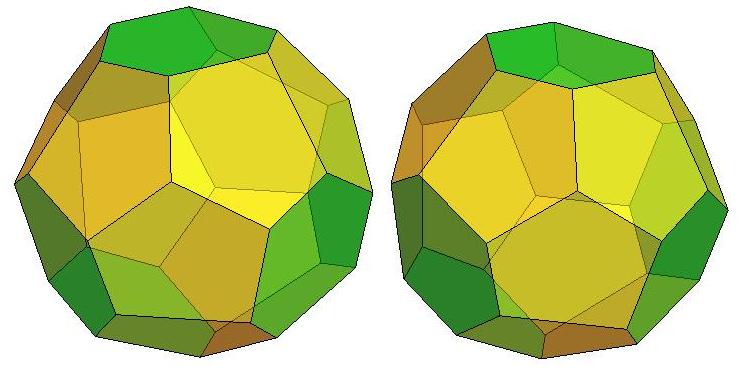
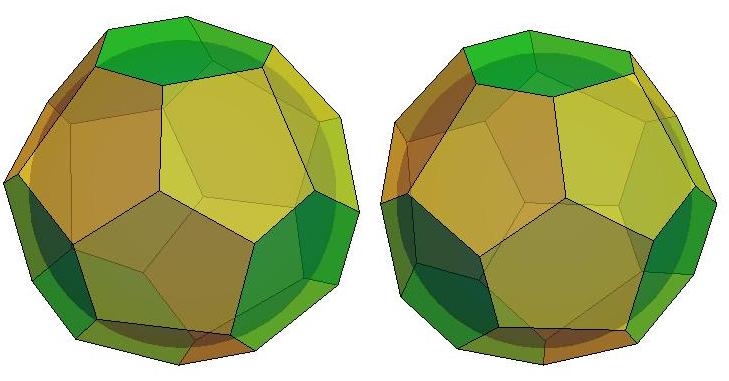
.jpg)
.jpg)
.jpg)
n=18
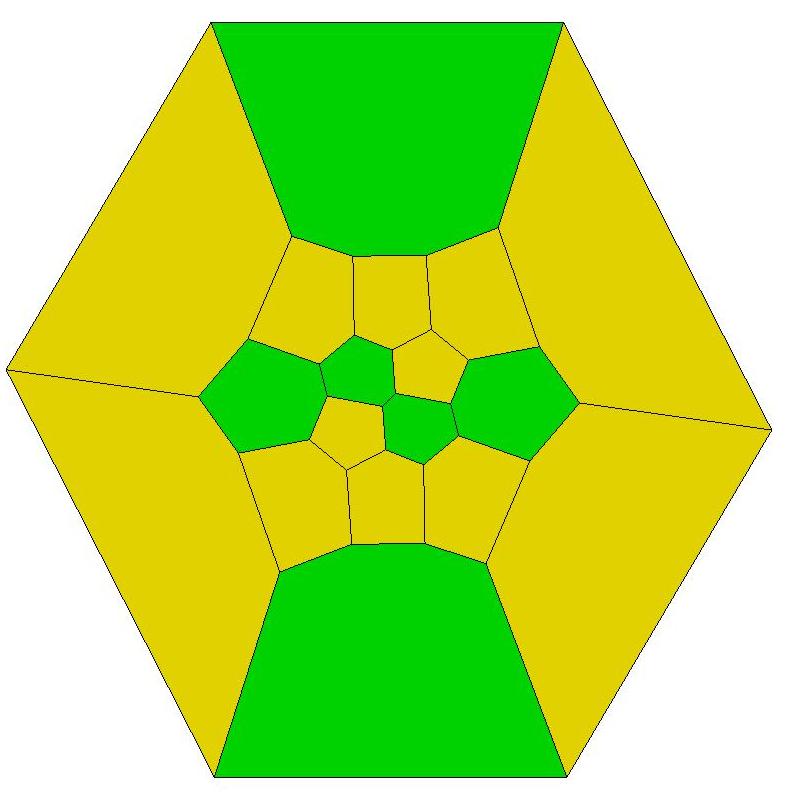
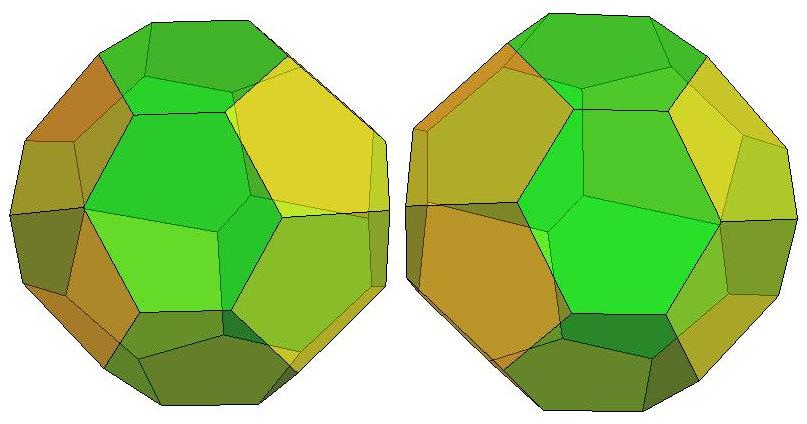
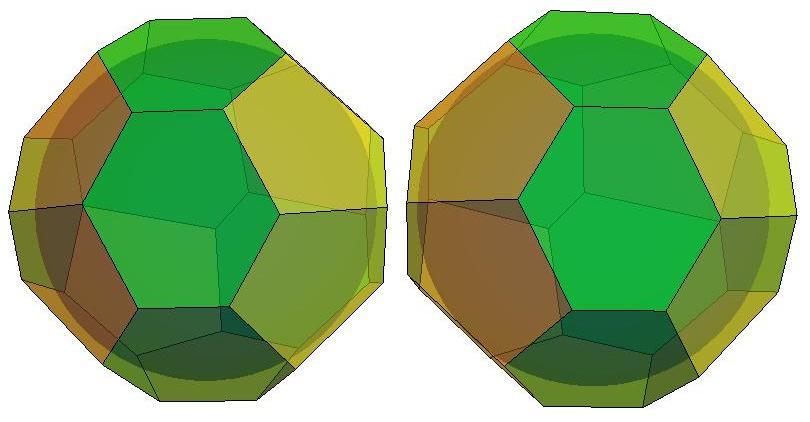
n=19
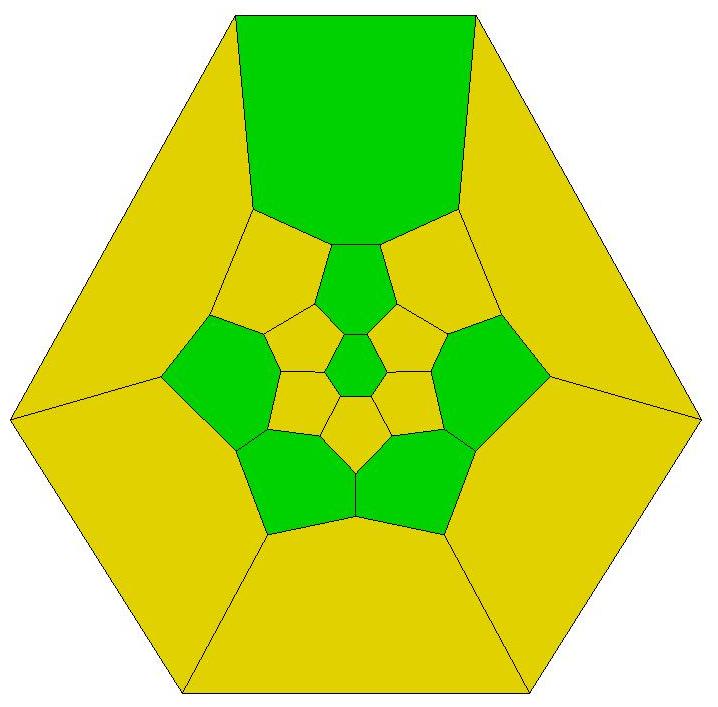
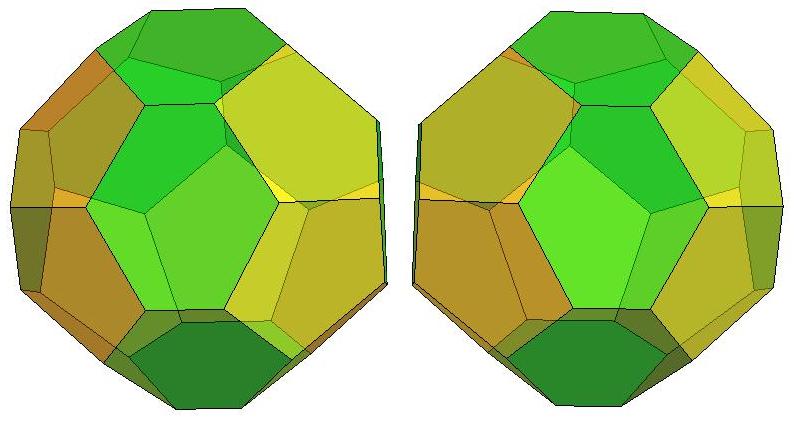
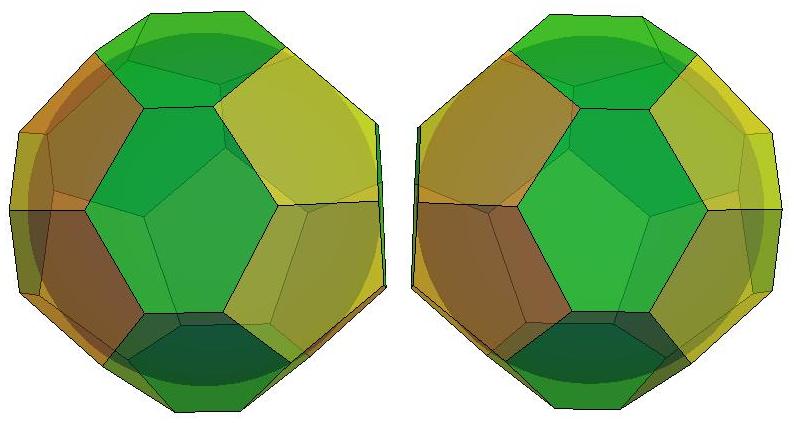
n=20
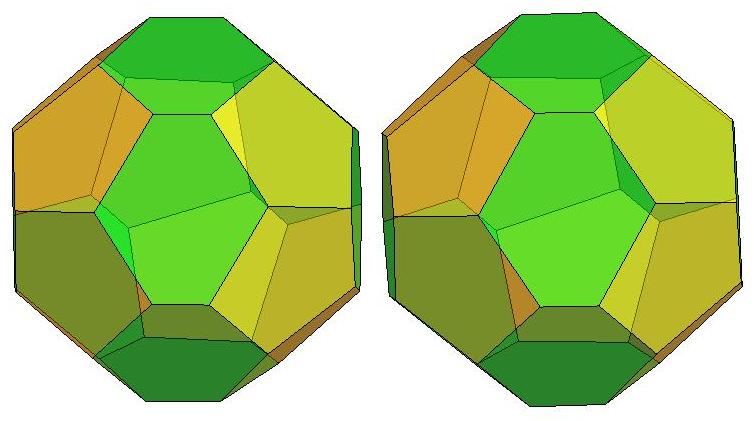
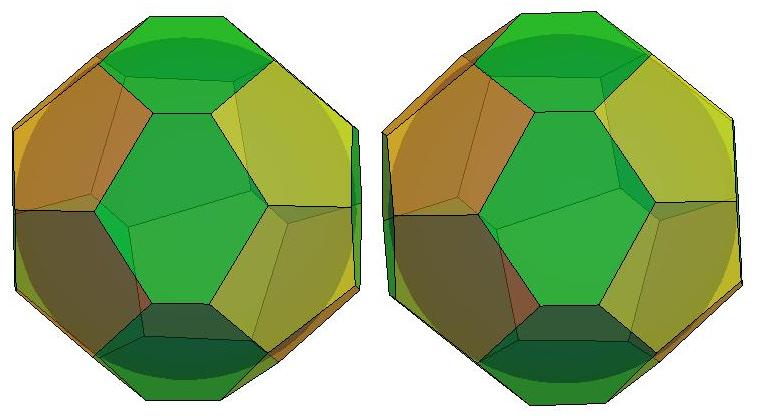
n=21
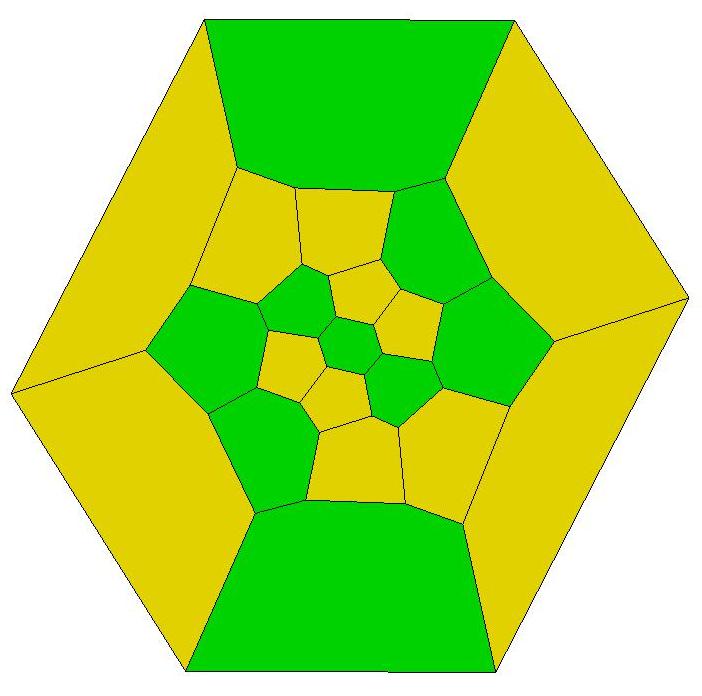
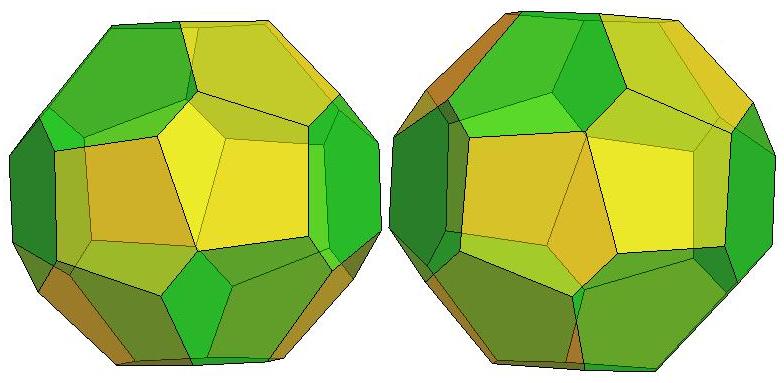
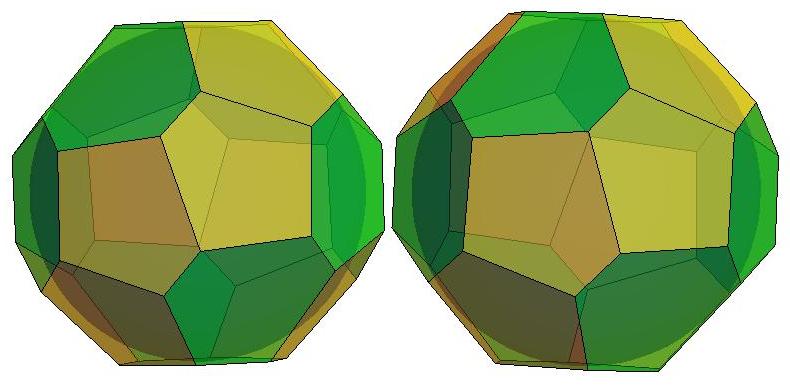
n=22
n=23
.jpg)
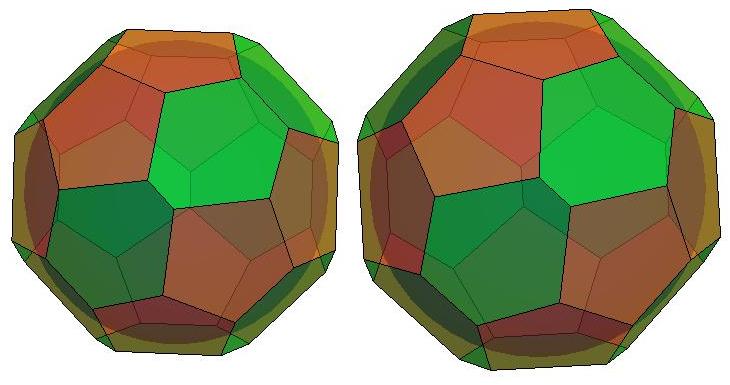
n=24
.jpg)
n=25
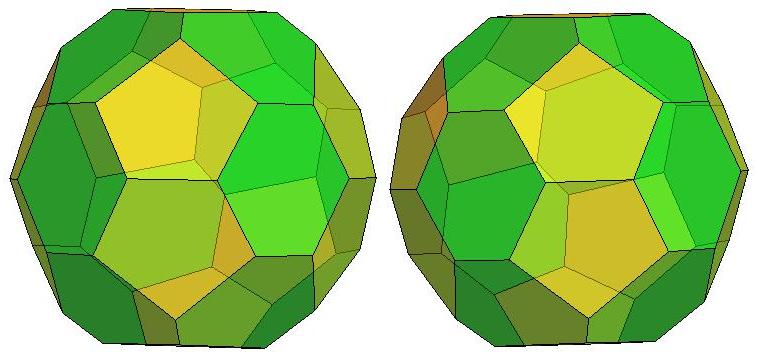
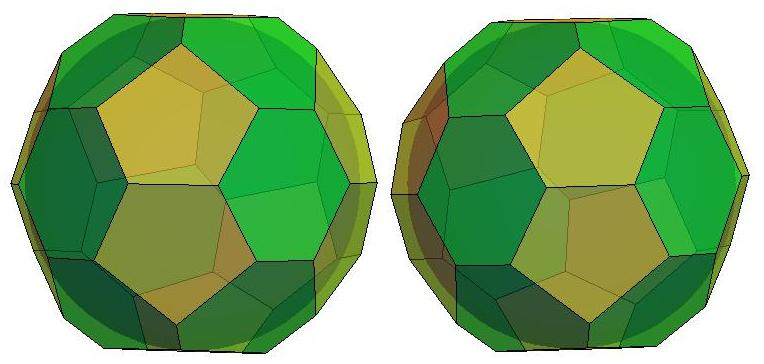
.jpg)
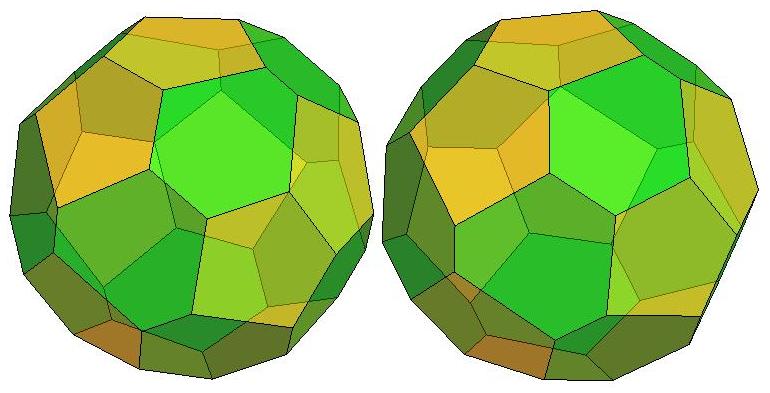
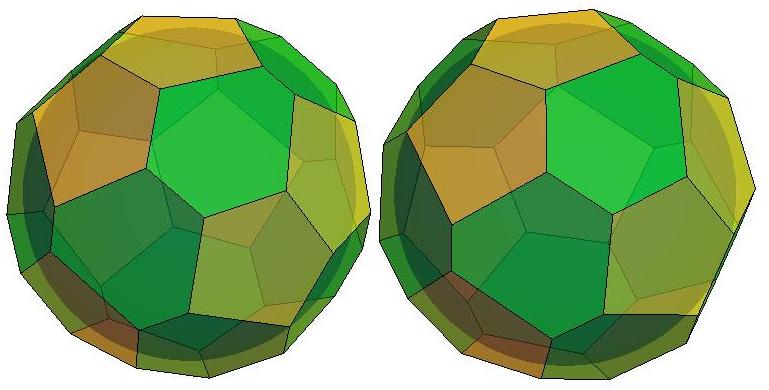
n=26
.jpg)
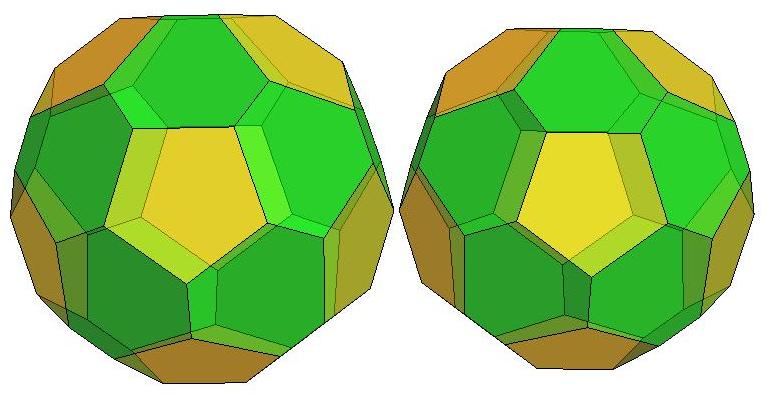
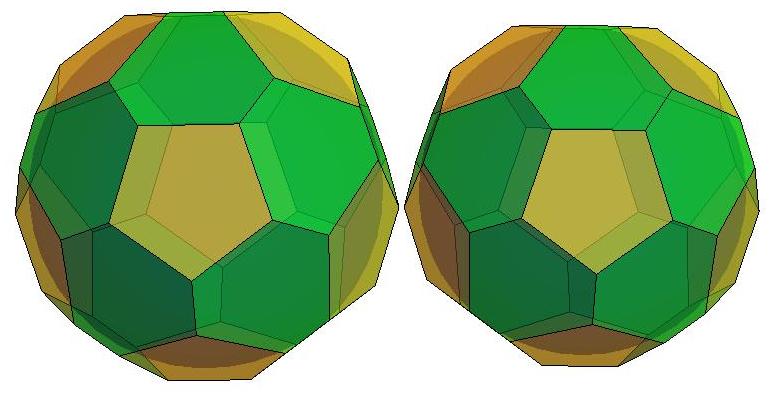
n=27
.jpg)
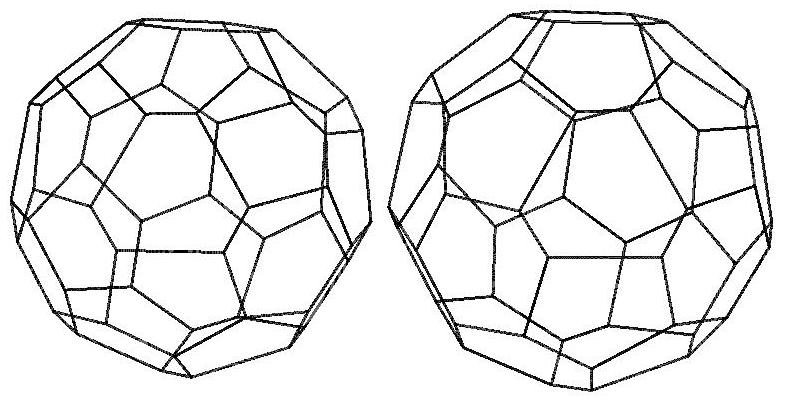
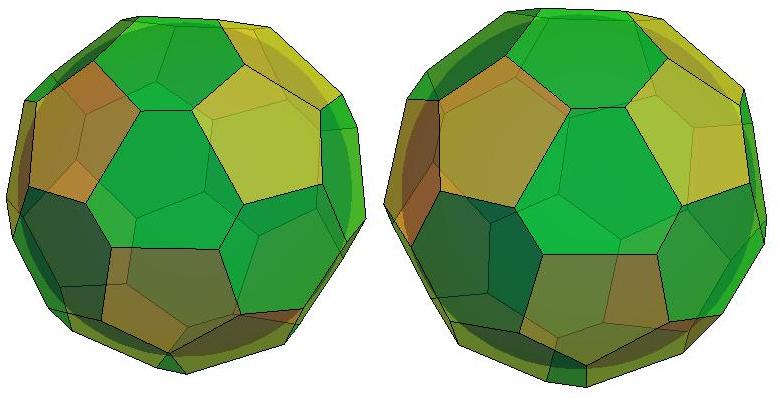
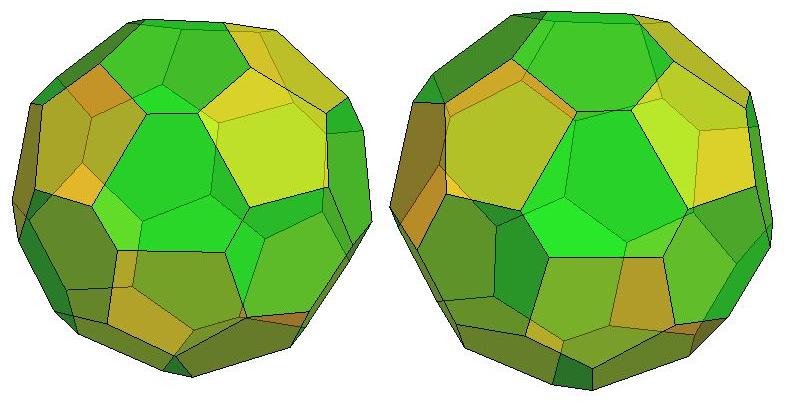

n=28
.jpg)
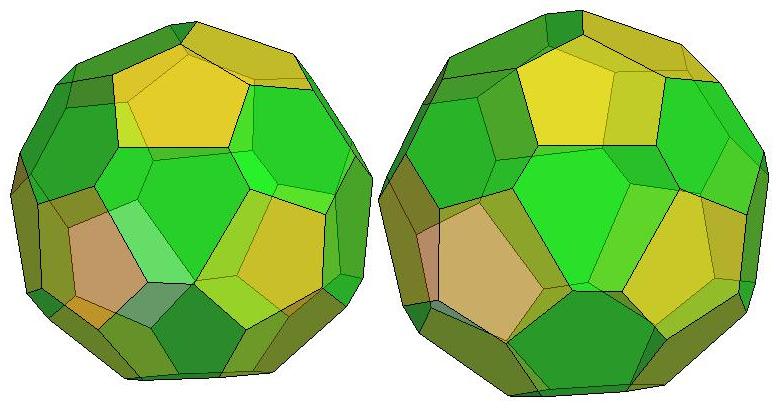
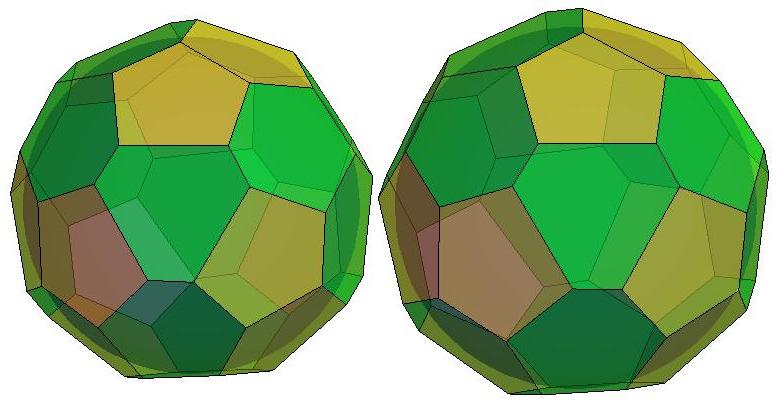
n=29
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
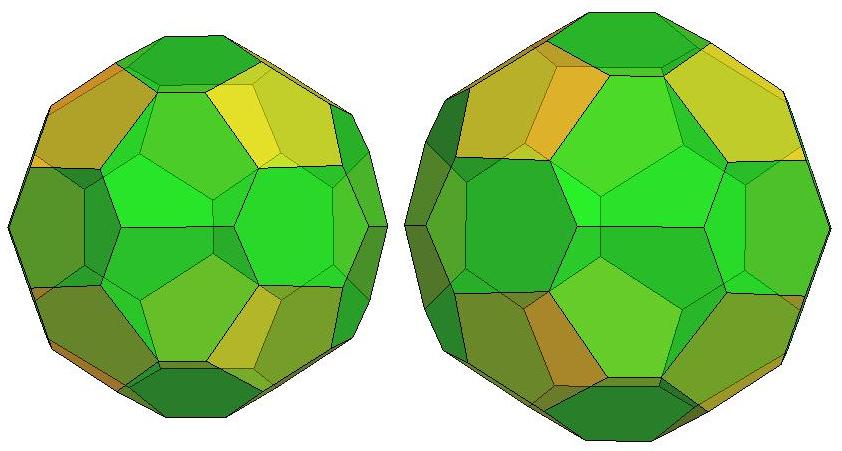
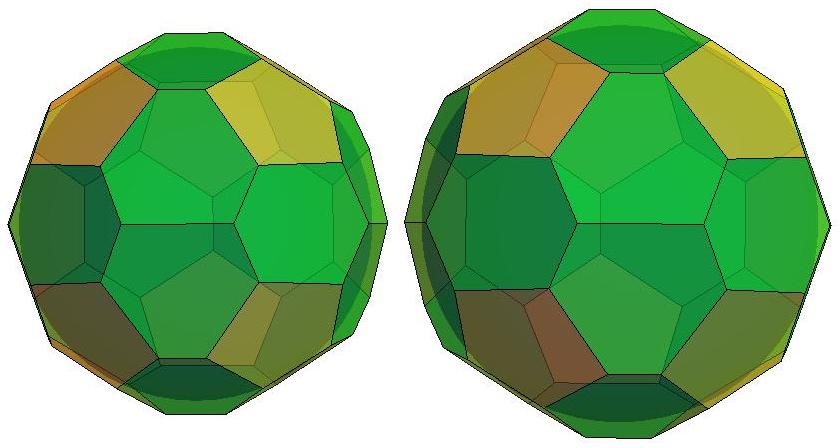
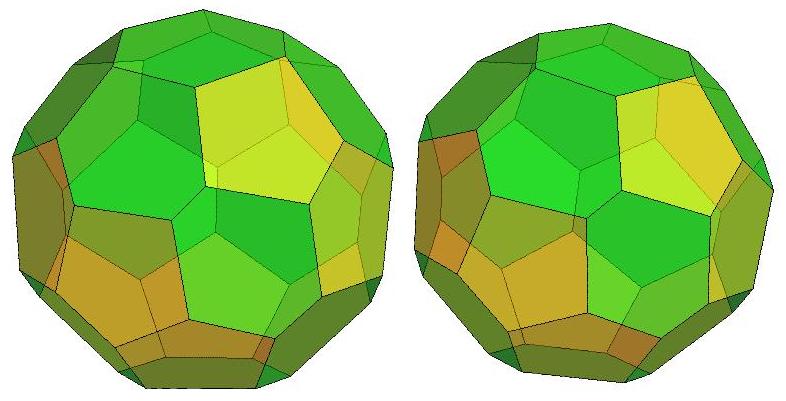
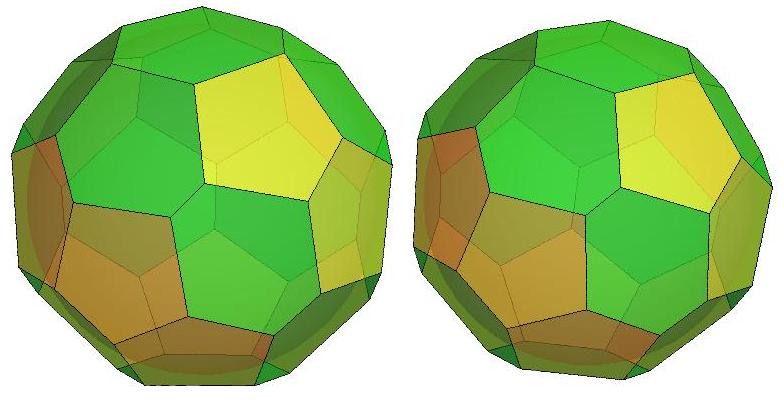
n=30
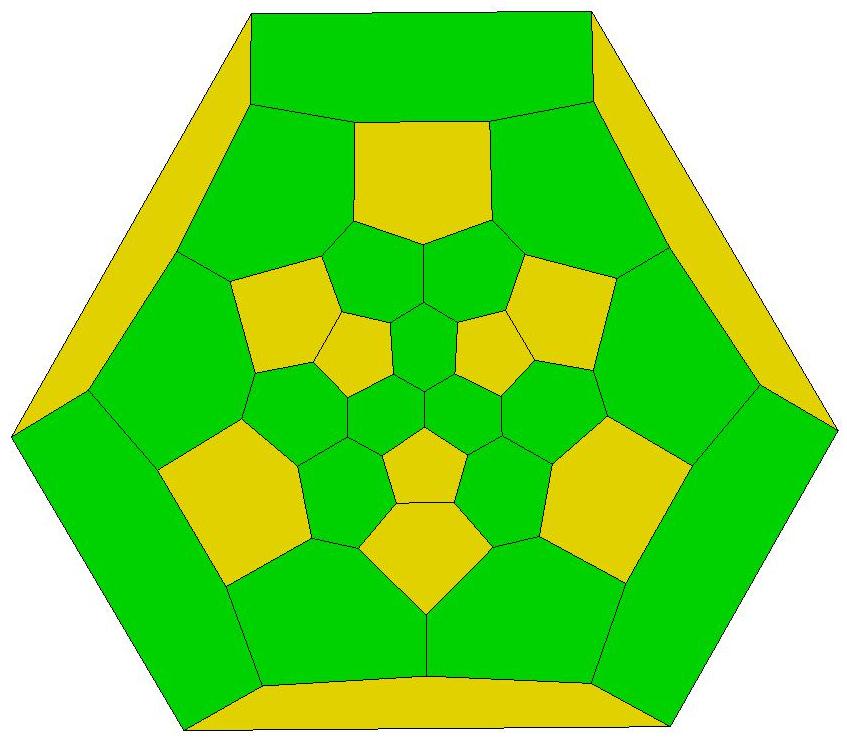
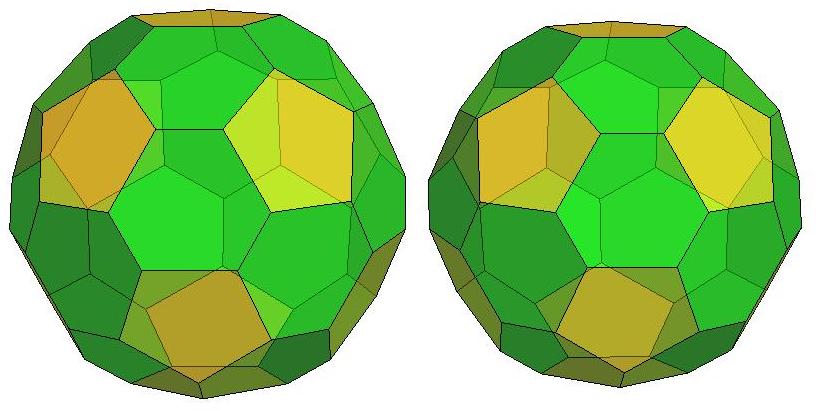
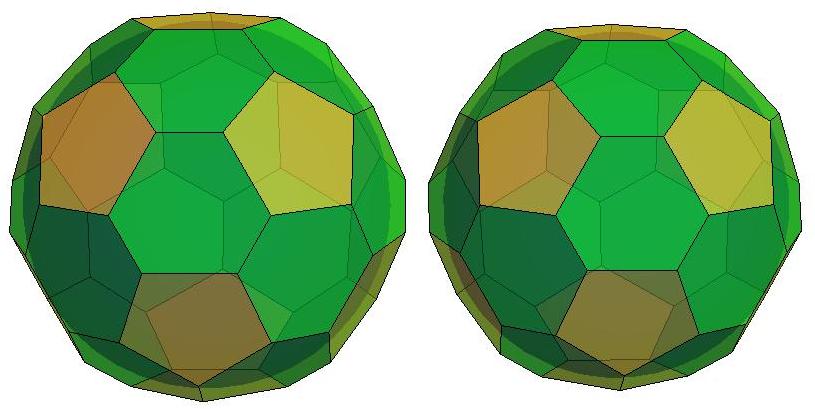
n=31

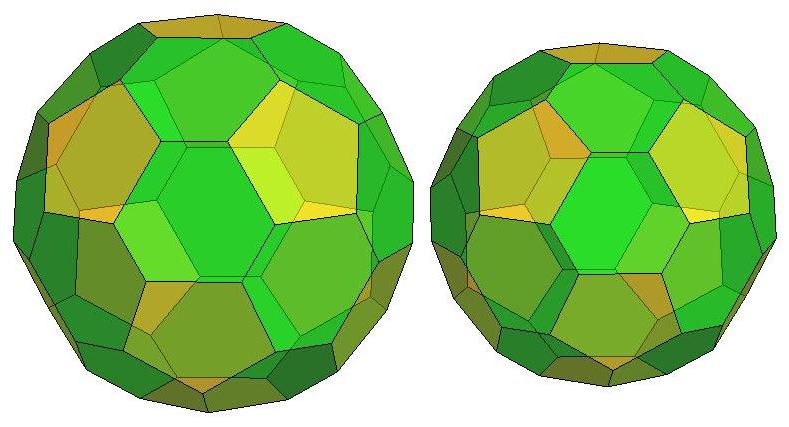
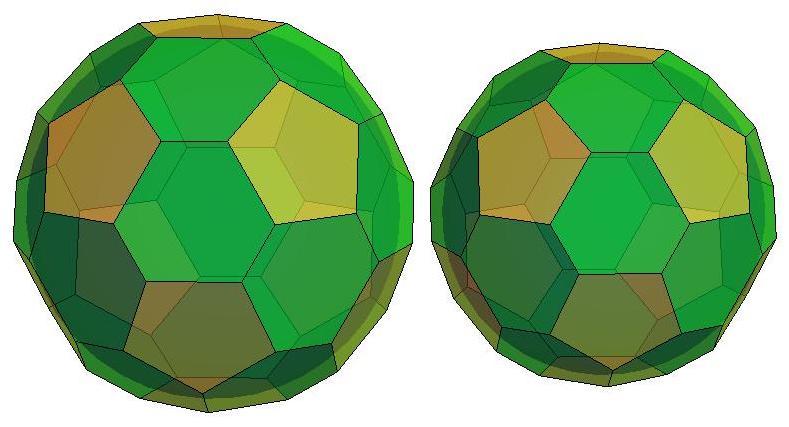
n=32
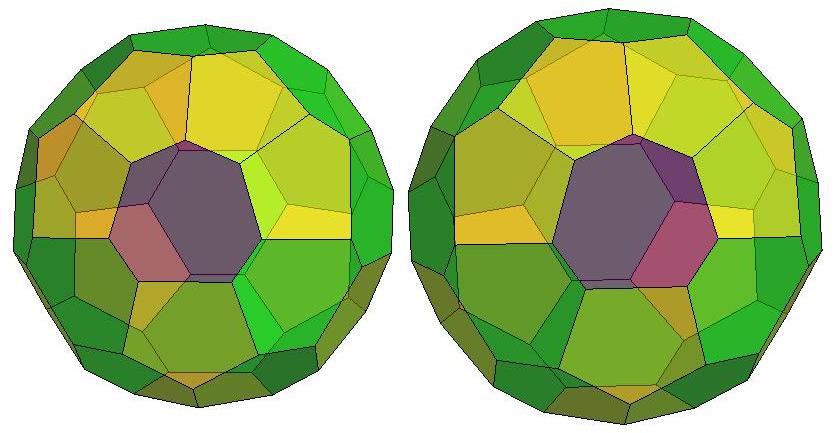
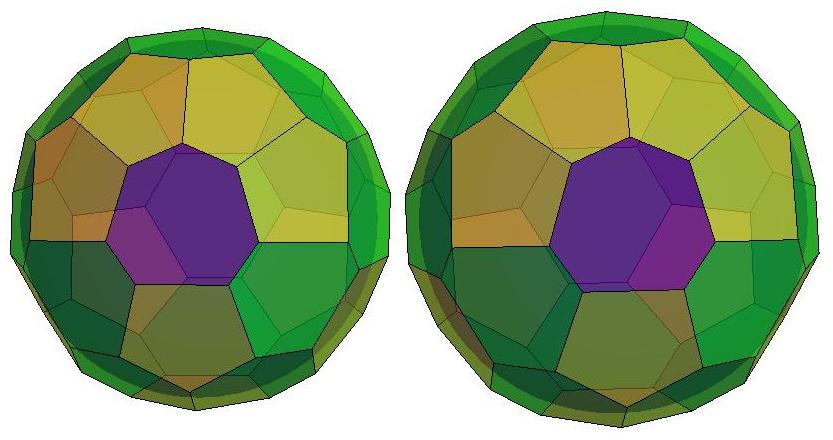
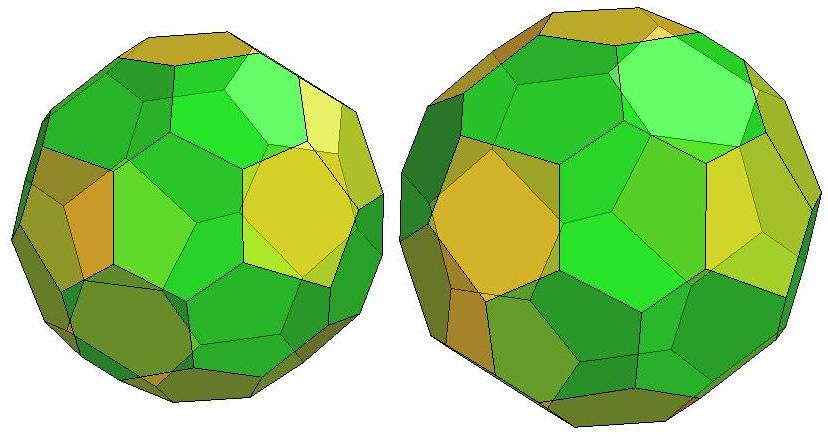
n=33
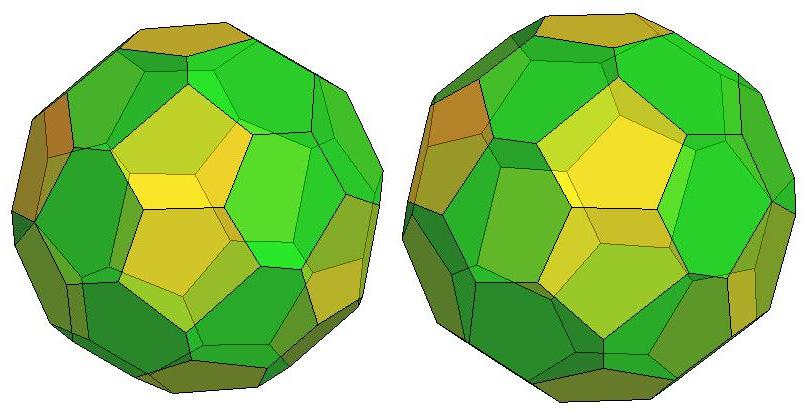
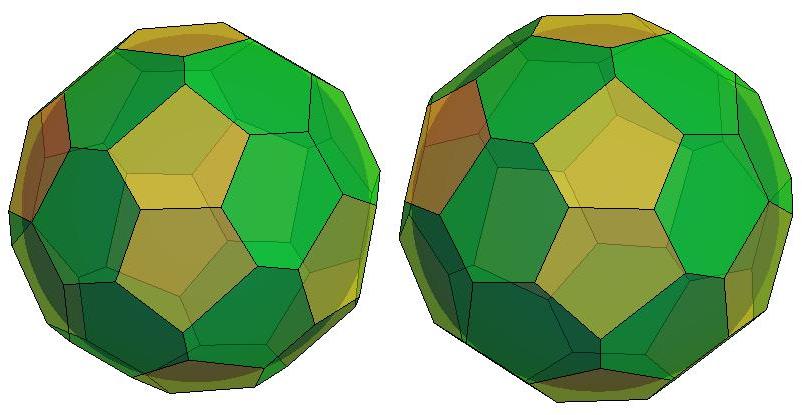
.jpg)
.jpg)
.jpg)
.jpg)
n=34
rot.jpg)
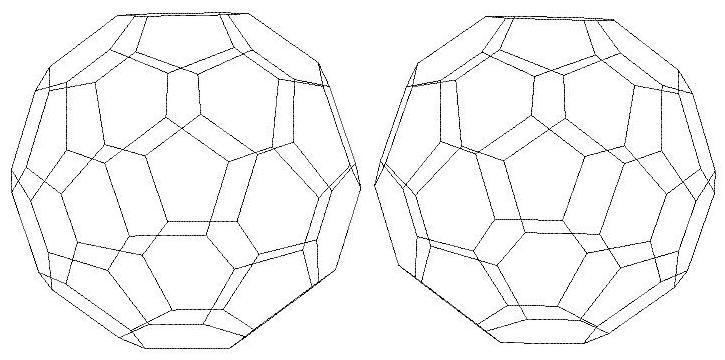
n=35
.jpg)
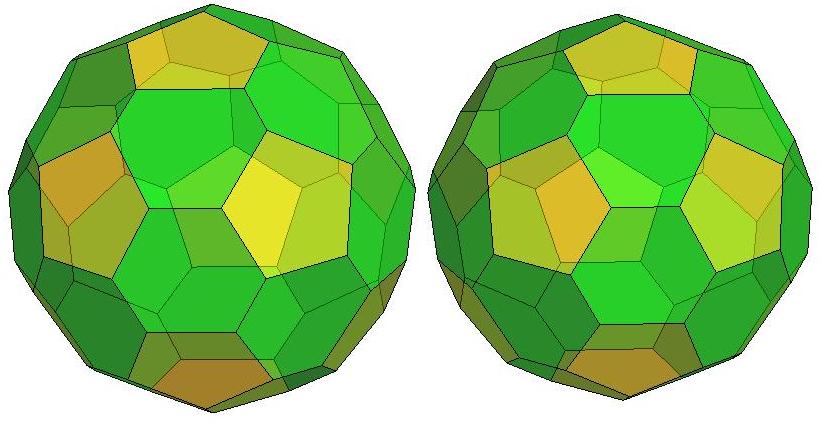
n=36
.jpg)
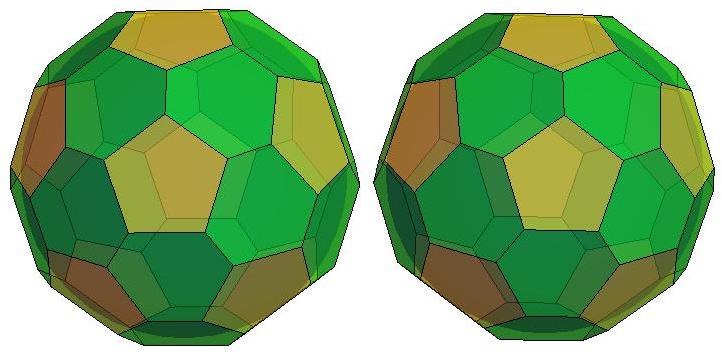
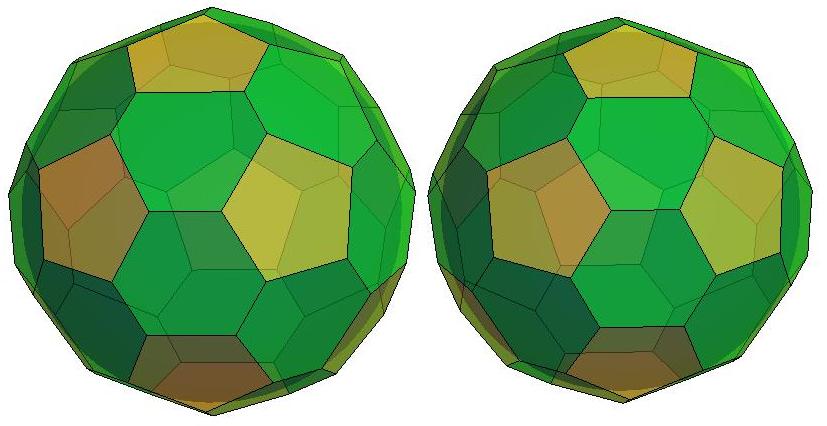
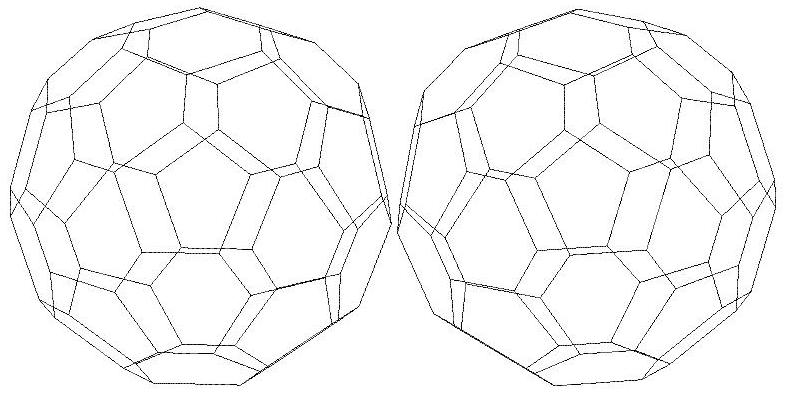
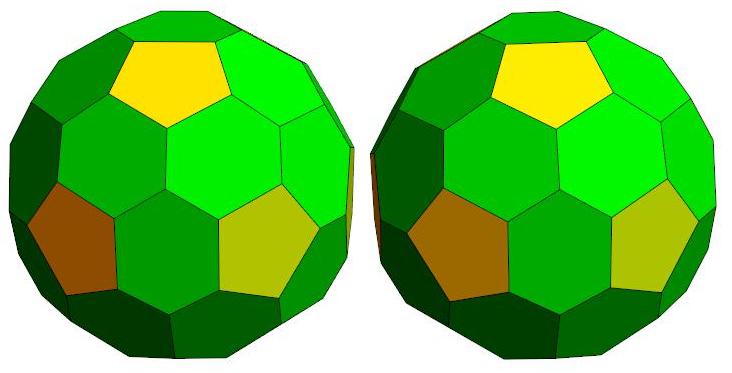
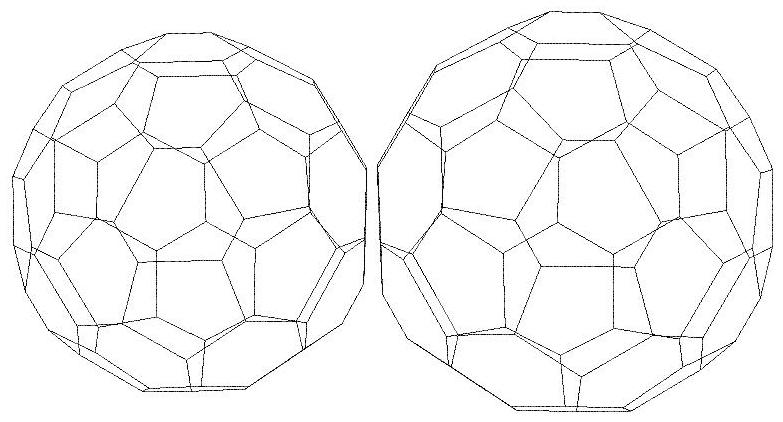
n=37
.jpg)
.jpg)
.jpg)
n=38
.jpg)
.jpg)
.jpg)
.jpg)
n=39
.jpg)
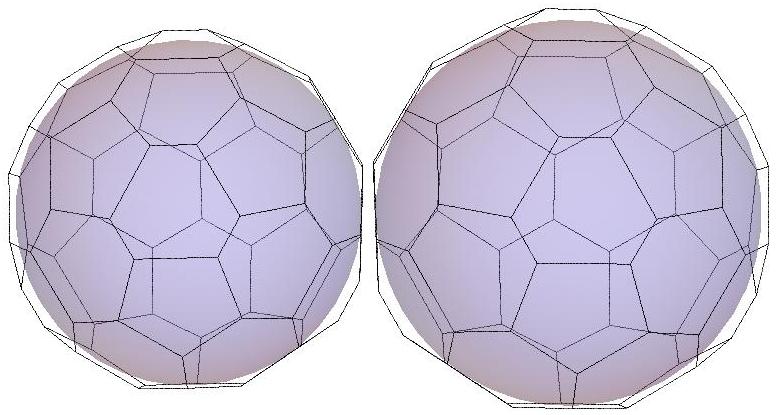
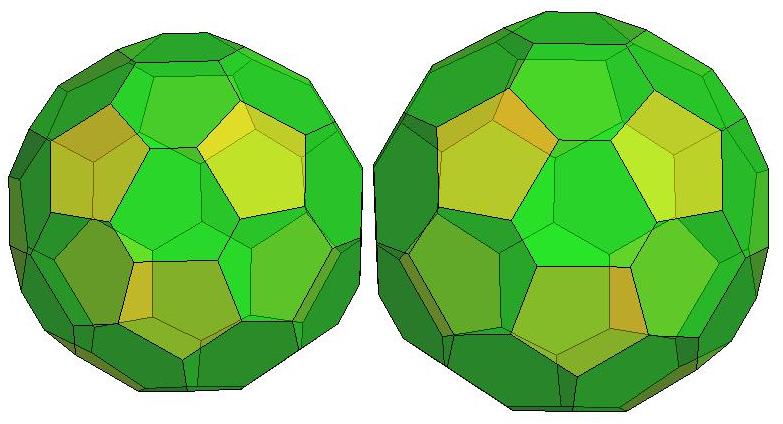
.jpg)
n=40
.jpg)
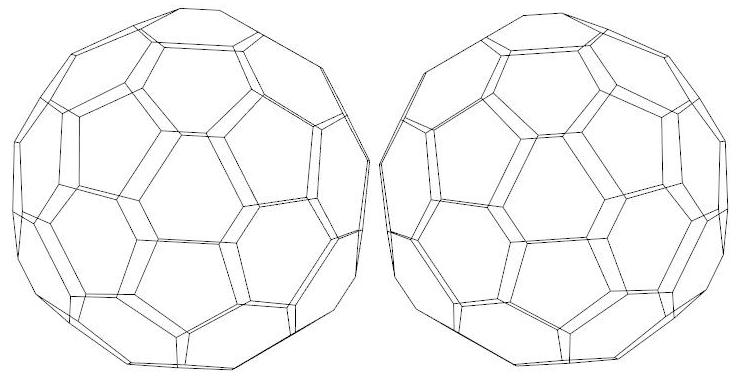
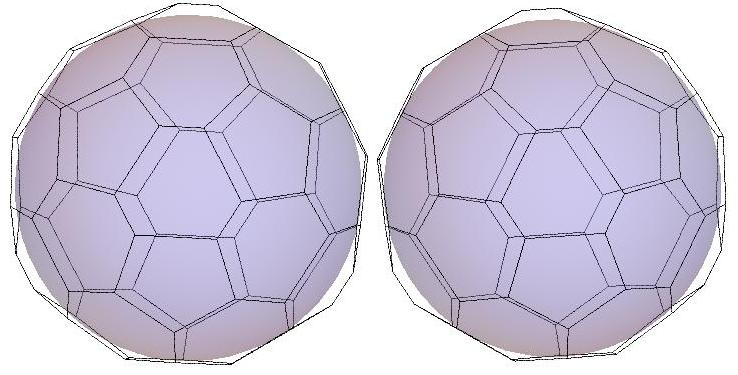
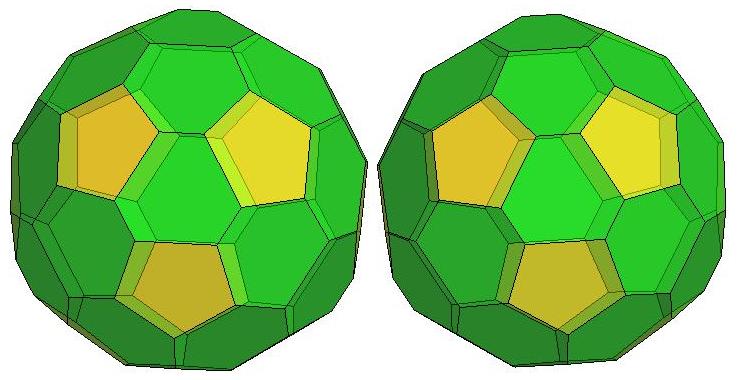
n=41
.jpg)
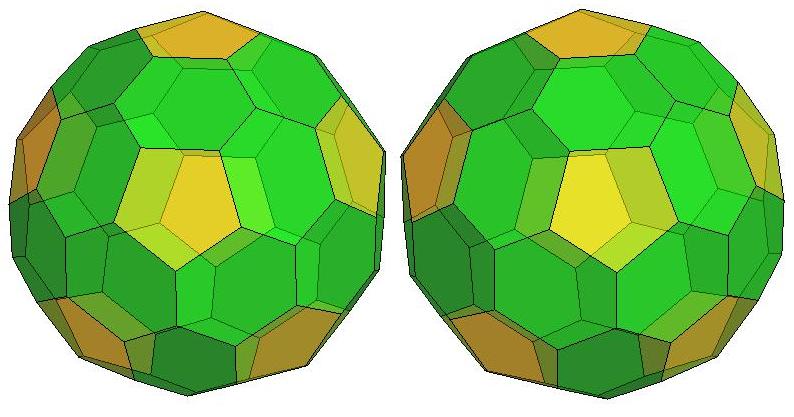
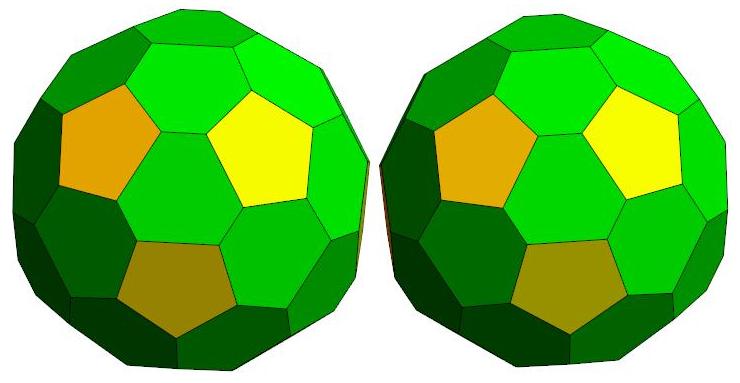
n=42
.jpg)
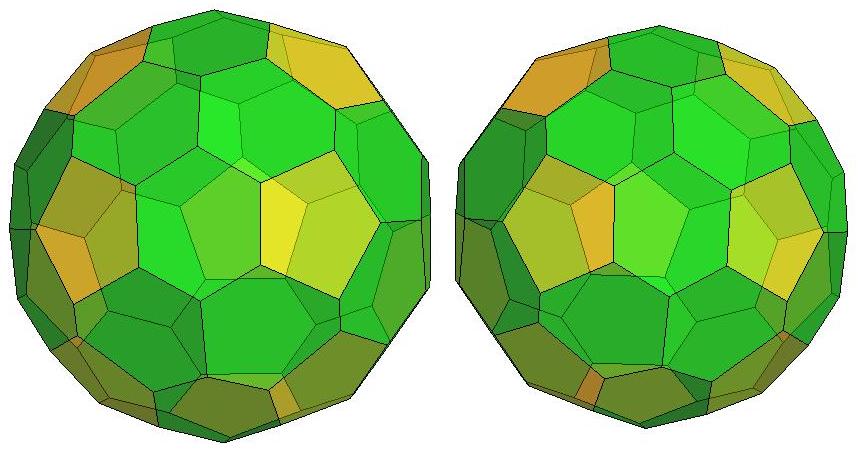
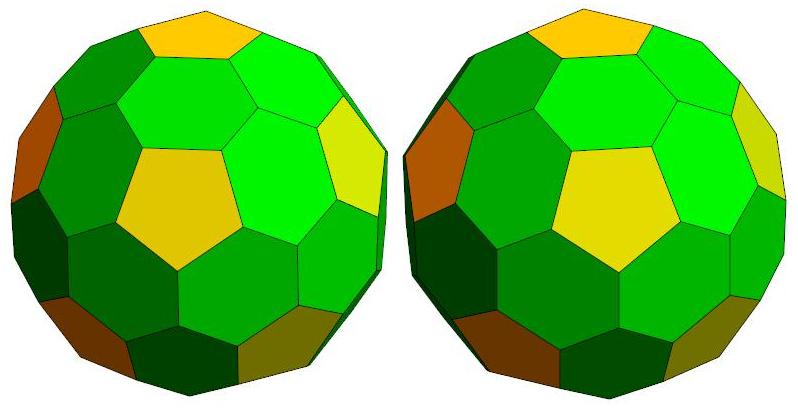
n=43
.jpg)
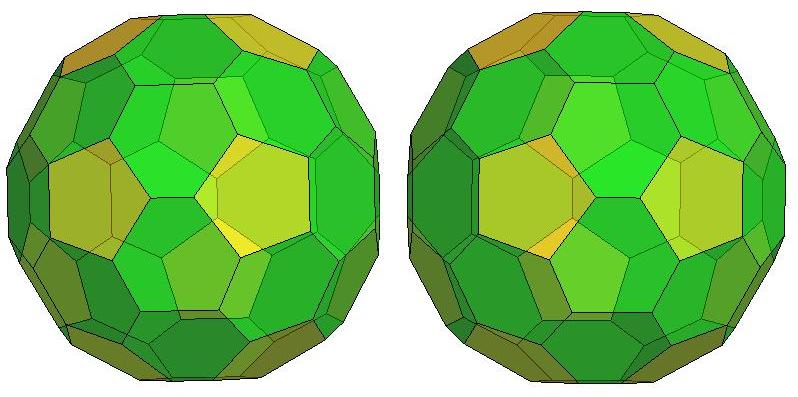
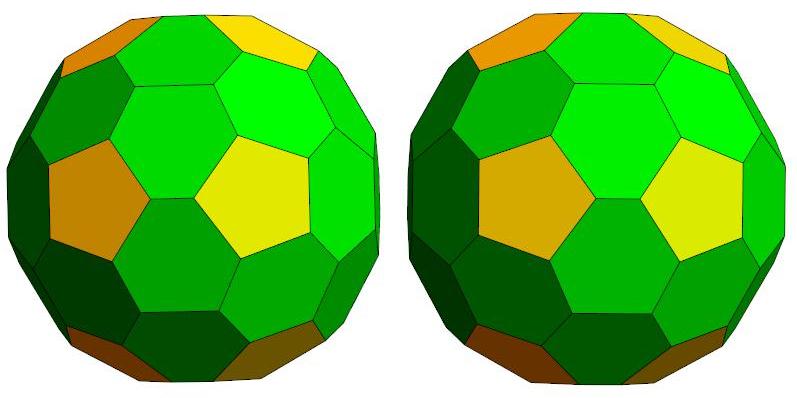
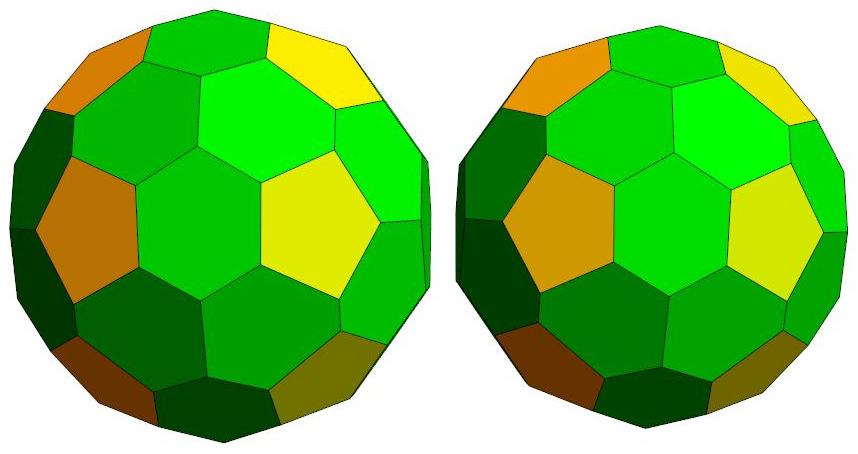
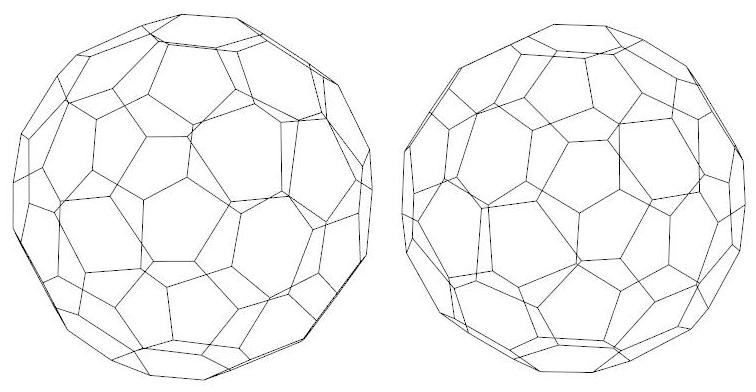
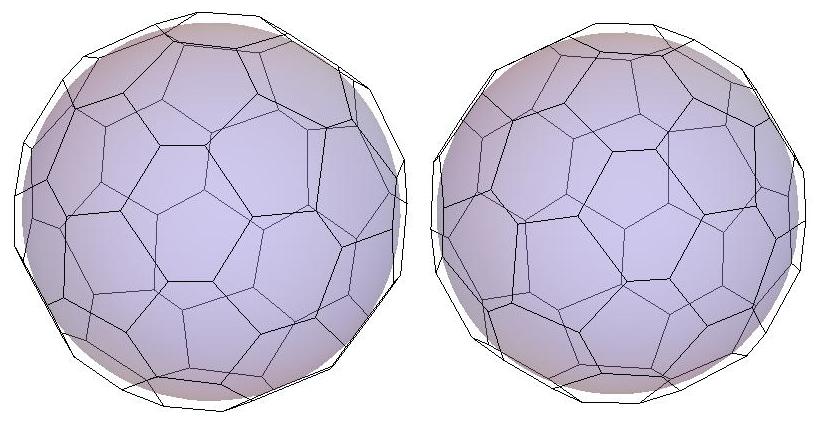
n=44
.jpg)
.jpg)
n=45
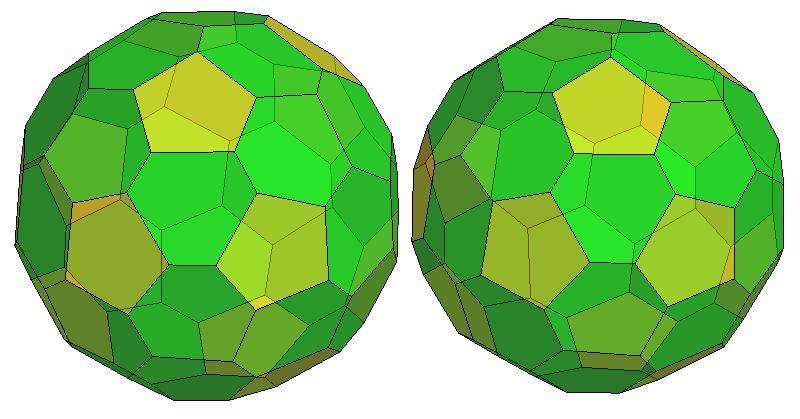
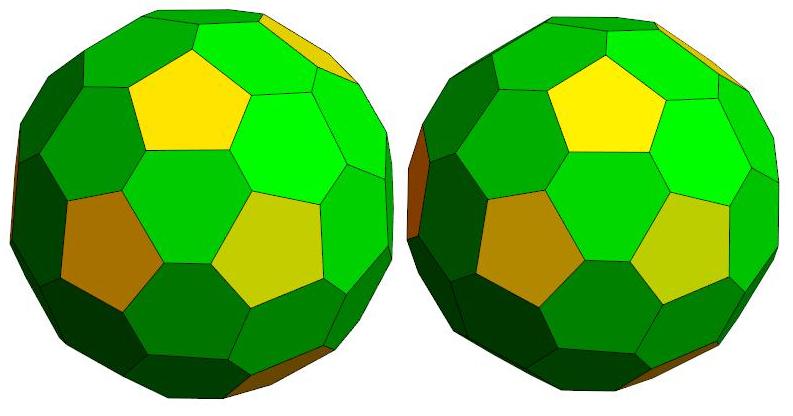
n=46
.jpg)
n=47

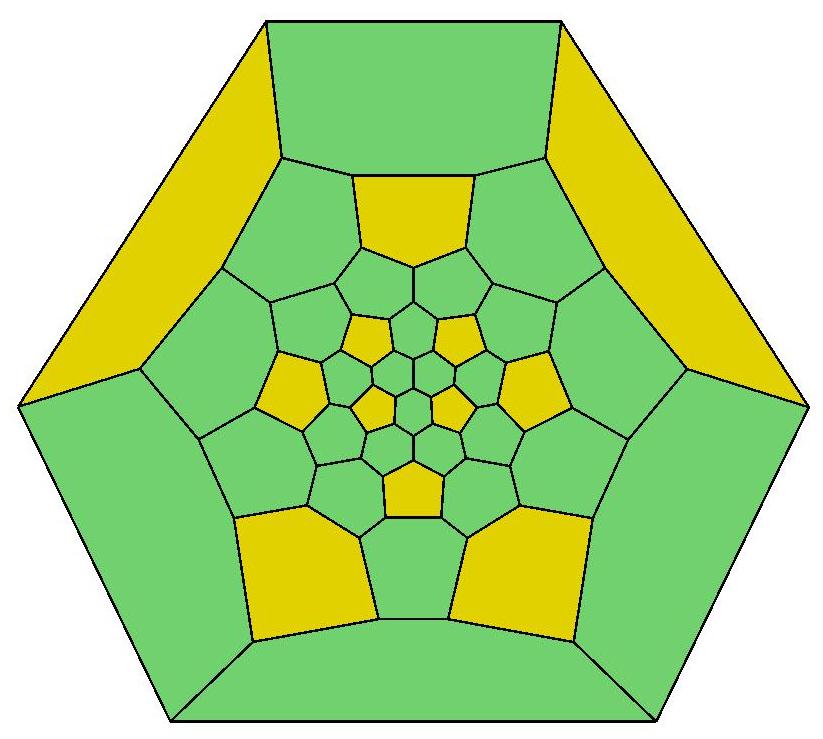
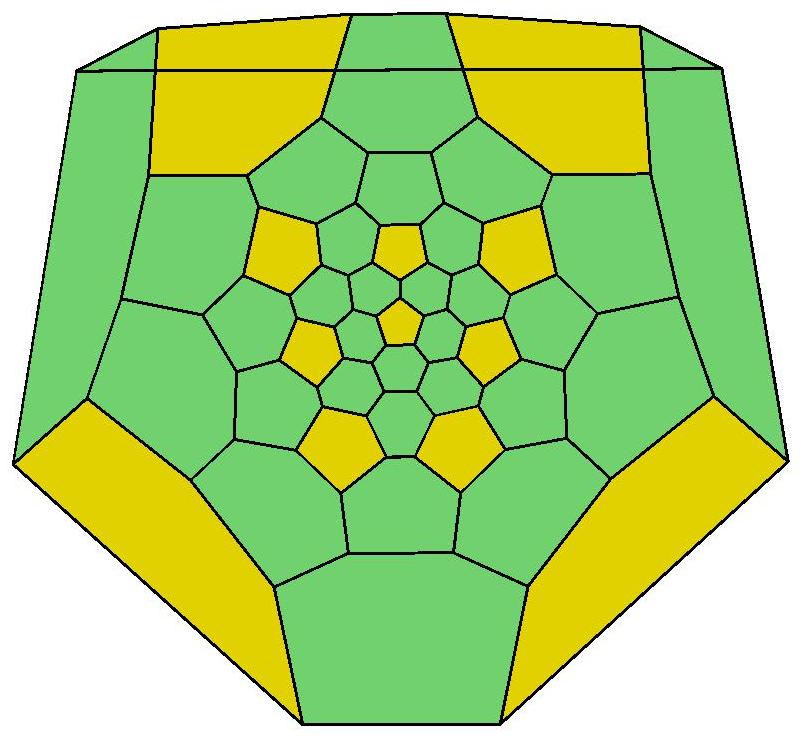
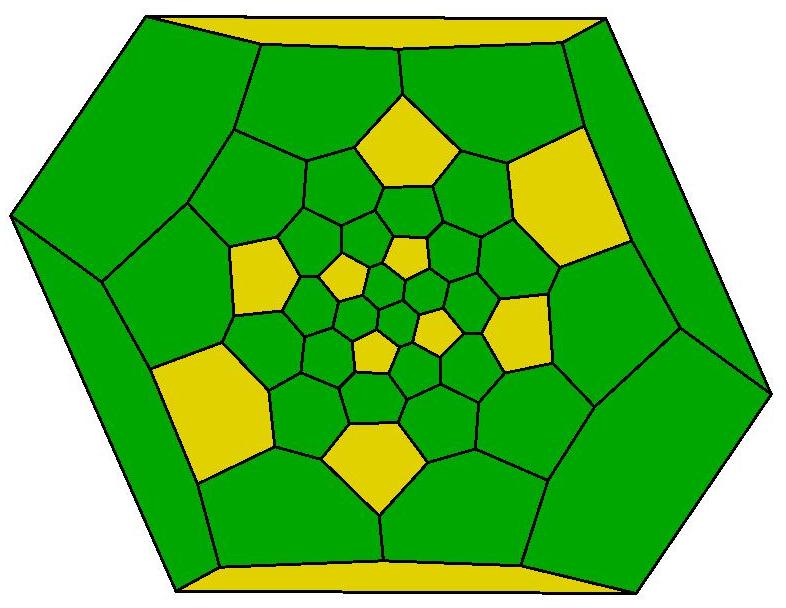
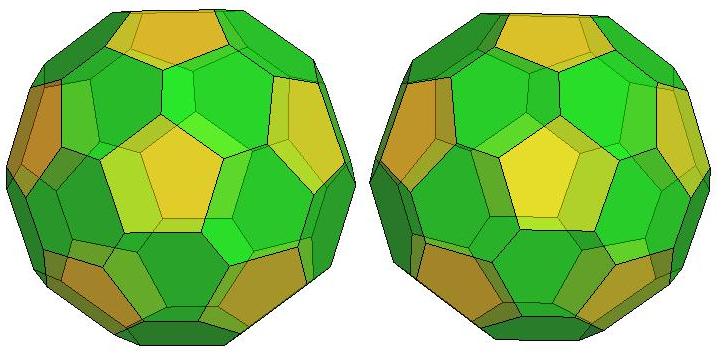
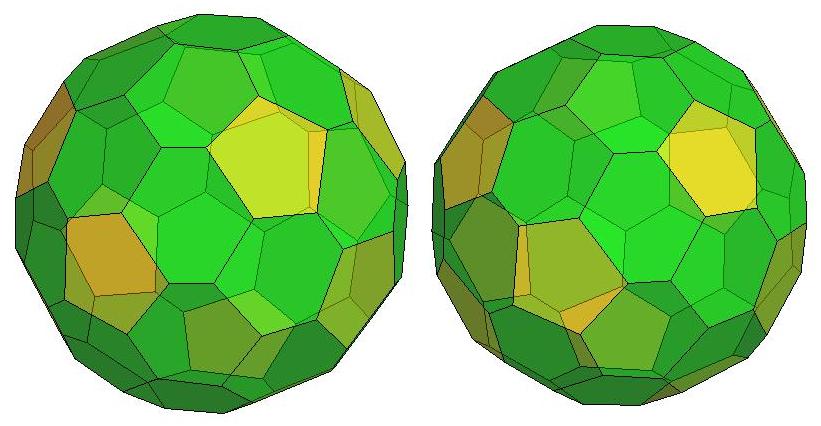
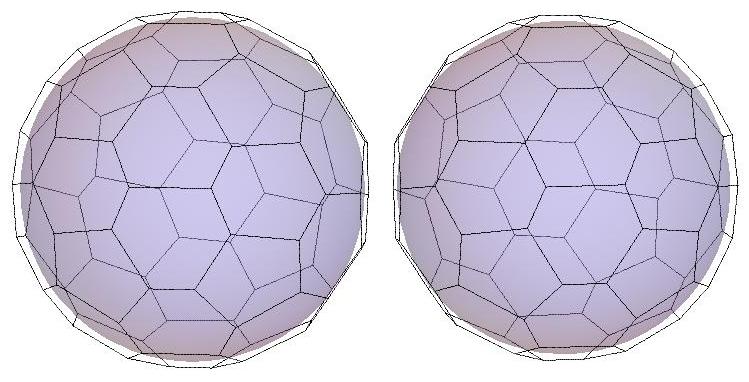
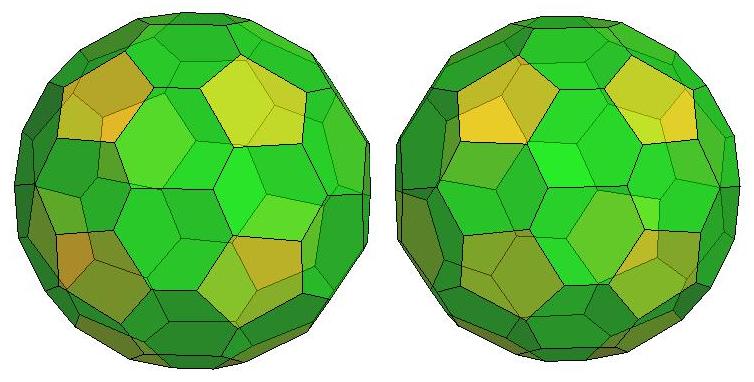
P44, probably the roundest polyhedron
with 44 faces
1986 IBM Computational Geometry Conference
Yorktown Heights, NY
If you recognize this conferee,
please let me know who she is!
I recall taping the P44 faces together just
the day before the conference. At the
conference, this young lady obligingly
agreed to relieve me of this model
(since it would have been hugely
inconvenient for me to fly home with it).
The problem of roundest polyhedra in R3 asks:
Which n-faced polyhedron has the smallest
ratio of S 3/V 2?
(S = surface area and V = volume.)
here as I.Q.. Because it is dimensionless, it is independent of scale.
In 1897, Minkowski proved that there exists a roundest polyhedron
for every n ≥ 4.
In 1899 it was proved by Lorenz Lindelöf that a
necessary condition for a polyhedron
P to be roundest is that
(i) P circumscribes a sphere,
and
(ii) this sphere is tangent to
the faces of
P at their
respective centroids.
For a polyhedron circumscribed about the unit sphere,
S/V = 27V = 9S.
Hence minimizing S 3/V 2
is equivalent to
minimizing S (or V).
It has long been conjectured — but never proved — that the
roundest
polyhedron is always simple,
i.e., that its vertices are all of degree three.
In 1986, I wrote a FORTRAN program called
'Lindelof' that repeatedly
tilts the faces of a polyhedron that
circumscribes the sphere until every
face is (almost
exactly) tangent to the sphere at its centroid.
I'll call this
state TAC (for "tangent at centroid").
The starting polyhedron in each
run was constructed by applying n
randomly oriented tangent planes to
the sphere and determinng their intersections
(although the program
also accepted pre-designed polyhedra as input).
In each iteration, every
face plane was tilted in a direction that would
reduce the gap between
its current centroid and its point of tangency.
For each n, the polyhedron
found to have the smallest area after a long sequence of
tilts was anointed
as the [probable] roundest.
I summarized my results for 4 ≤ n ≤ 35
and for n = 42 in an
IBM conference
report:
'A Defect-Correction Algorithm for Minimizing the Volume
of a
Simple Polyhedron Which Circumscribes a Sphere'
and in a May 1986
supplement
that describes conjectured solutions for
36 ≤ n ≤ 41
and n = 43.
(This supplement includes numerical data derived
from an analysis by
William Tutte
of the asymptotic number of simple
polyhedra as a function of the
number n of faces.)
In August, 1986, I ran Lindelof for the last time and derived
solutions
for n = 45, 46, and 47.
Below are links to sets of face templates for n = 8, 25, 33, and 44.
You can use these templates to construct physical models of these
examples of conjectured 'roundest' polyhedra.
For the case n = 8,
I have provided templates only for faces 1, 2, 3, and 4,
since faces
5, 6, 7, and 8 are congruent to faces 1, 2, 3, and 4, respectively.
For n = 8, 25, and 44, each vertex
of the template is labeled by an
integer,
but for the case n = 33, each edge is labeled by an integer.
template for n = 8: face 1
template for n = 8: face 2
template for n = 8: face 3
template for n = 8: face 4
templates for n = 25: ALL faces
templates for n = 33: ALL faces
templates for n = 44:
faces 1, 2, 3
templates for n = 44:
faces 6, 8, 14
templates for n = 44:
faces 7, 9, 10
templates for n = 44:
faces 5, 11, 12, 34
templates for n = 44:
faces 13, 15, 16
templates for n = 44:
faces 17, 18, 41
templates for n = 44:
faces 19, 20, 44
templates for n = 44:
faces 21, 22, 23
templates for n = 44:
faces 4, 24, 26
templates for n = 44:
faces 25, 31, 33
templates for n = 44:
faces 27, 28, 29, 30
templates for n = 44:
faces 35, 36, 37
templates for n = 44:
faces 32, 38, 40
templates for n = 44:
faces 39, 42, 43

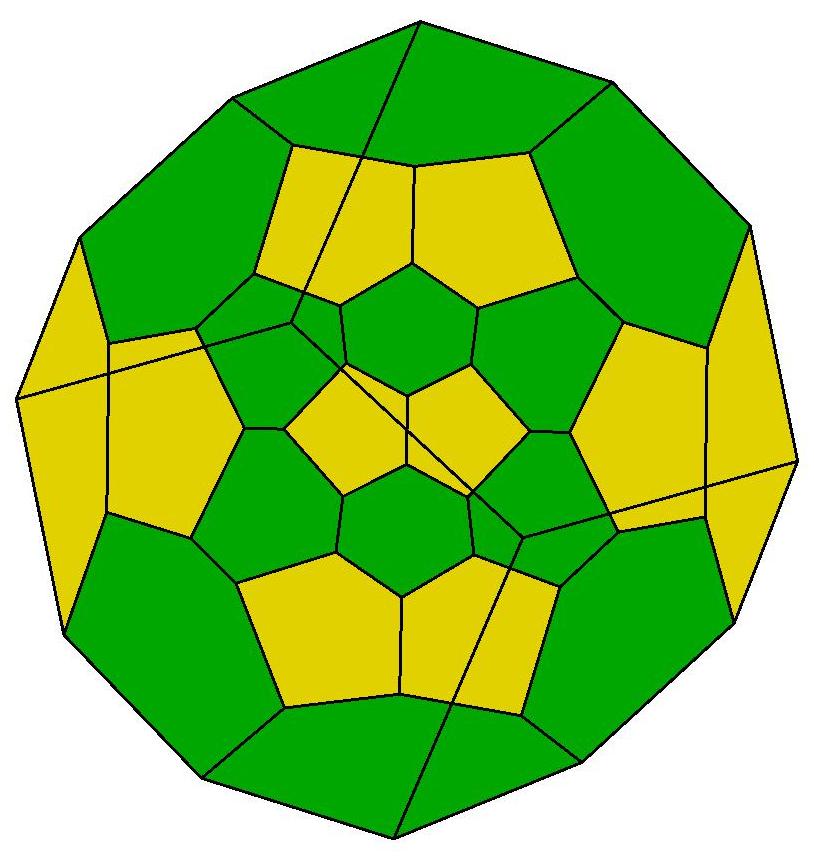
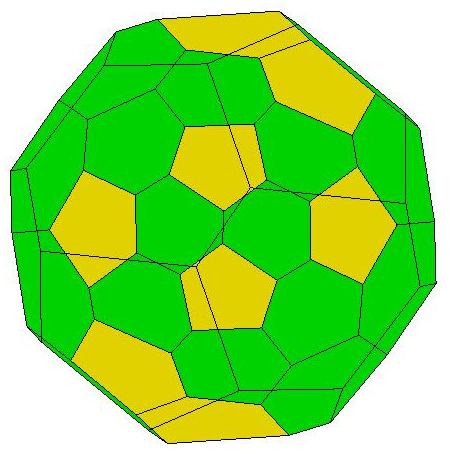
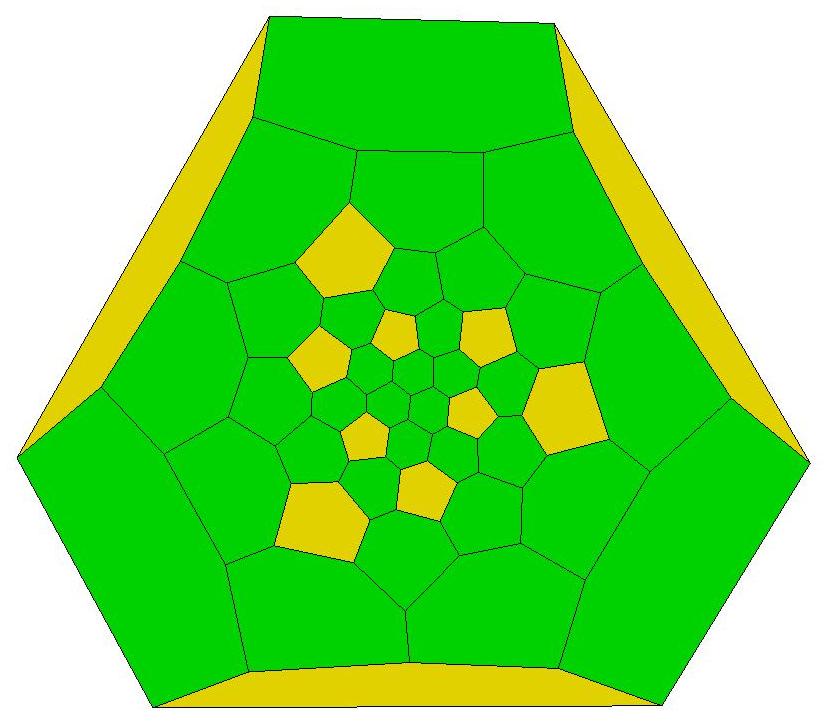
roundest polyhedron with 33 faces, is composed of
one heptagon (green), thirteen pentagons (yellow),
and nineteen hexagons (red-orange).
29 of the 33 faces of P33 define a connected assembly
with the same combinatorial structure as the faces of
the 'soccer ball' polyhedron (truncated icosahedron).
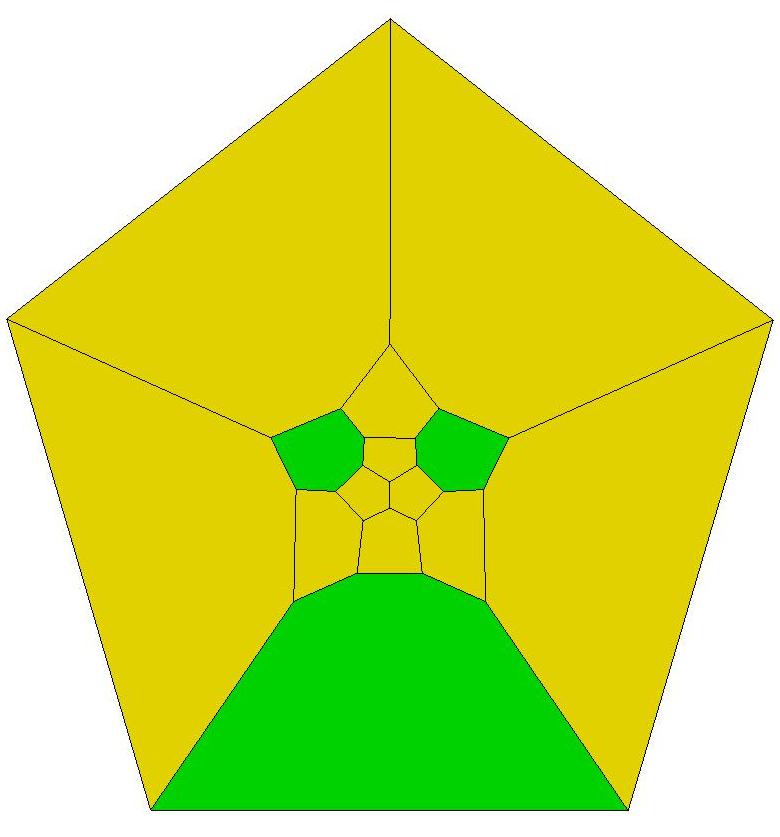
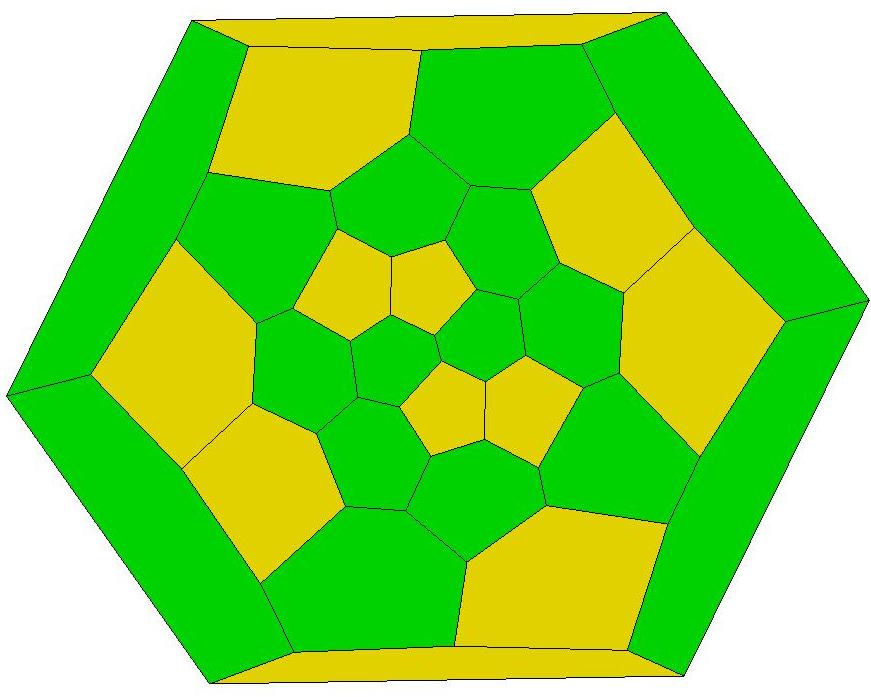
Below is a Schlegel diagram of P33:
.jpg)
To view a
sequence of eight rotated images of P33,
set the magnification at 80%.
I thank Joseph Malkevitch, who is himself a prolific geometer,

Joseph Malkovitch
for his 2015 article about the work of Victor Klee.
My own interest in roundest polyhedra was kindled in 1972 when I first saw
Klee's
two films about geometry,
'Shapes of the Future — Some Unsolved Problems
in Geometry'. Shortly afterwards Prof. Klee (1925-2007)
gave me copies of the filmscript
booklets for these two films,
Part I: Two Dimensions and
Part II: Three Dimensions.
With the permission of the
Mathematical Association of America,
I have made
digital copies of these films and uploaded them
to YouTube:
Part I: Two Dimensions (YouTube video)
and
Part II: Three Dimensions. (YouTube video)
I met Michael Goldberg several times at AMS meetings in the late sixties.
We
discussed minimal surfaces and Voronoi polyhedra, but unfortunately
he never
brought up the subject of roundest polyhedra,
in which I had a growing interest.
Like Victor Klee, Michael was an unusually modest man.
I greatly regret that
he never mentioned to me either of his
groundbreaking publications about polyhedra:
'The Isoperimetric Problem for Polyhedra'
(1934)
and
'A Class of Multisymmetric Polyhedra'
(1937).
In 1985 I discovered Goldberg's 1935 article, but only in 1991,
when I bought
Ian Stewart's wonderfully witty book about mathematics,
"Game, Set, and Math",
did I learn of Michael's 1937 article
introducing what are now
called
Goldberg
polyhedra, a class of polyhedra based on the regular
icosahedron.
Donald Caspar and Aaron Klug independently
rediscovered Goldberg polyhedra
in 1962.
They are related to the structure of several common viruses
and are described
in the Caspar-Klug publication,
"Physical Principles in the Construction of Regular
Viruses",
Cold Spring Harbor Symp. Quant. Biol. 27, pp. 1-24
(cf.
VIRUSWORLD).
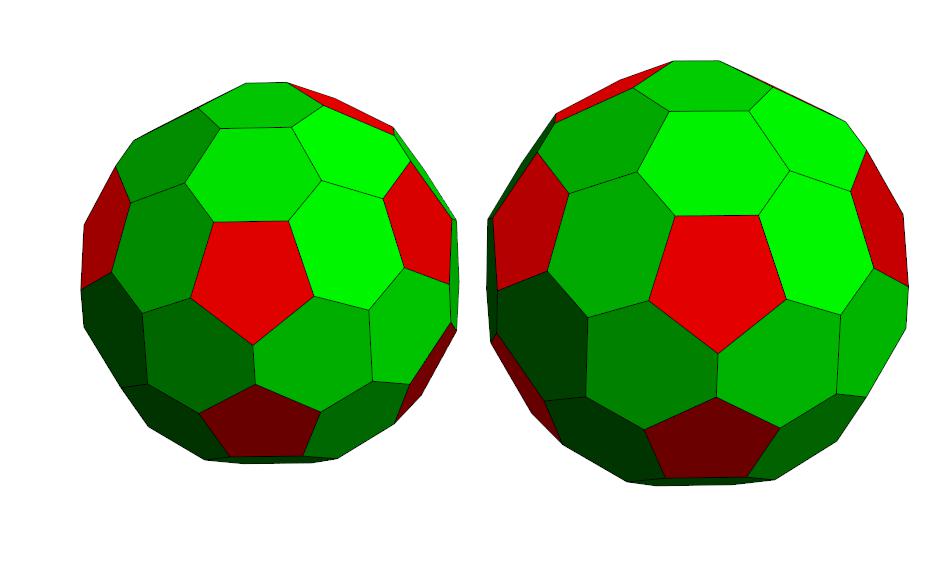
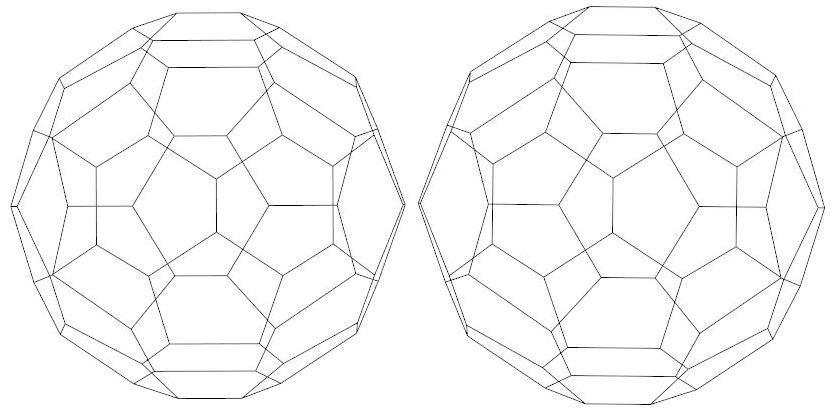
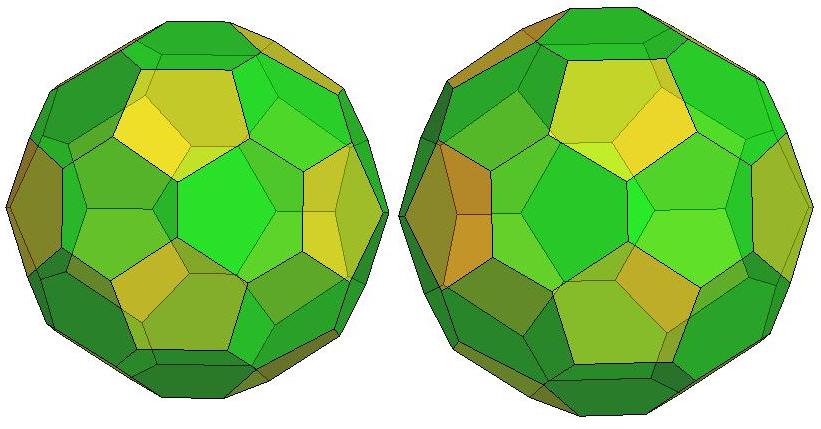
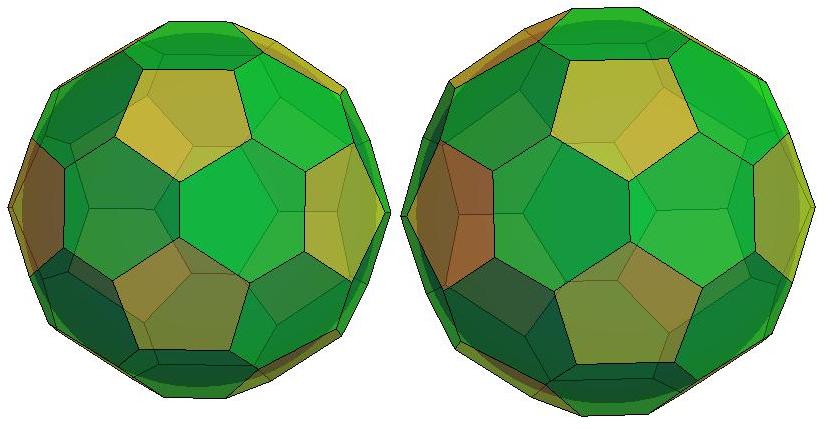
Front view of P44
Rear view of P44
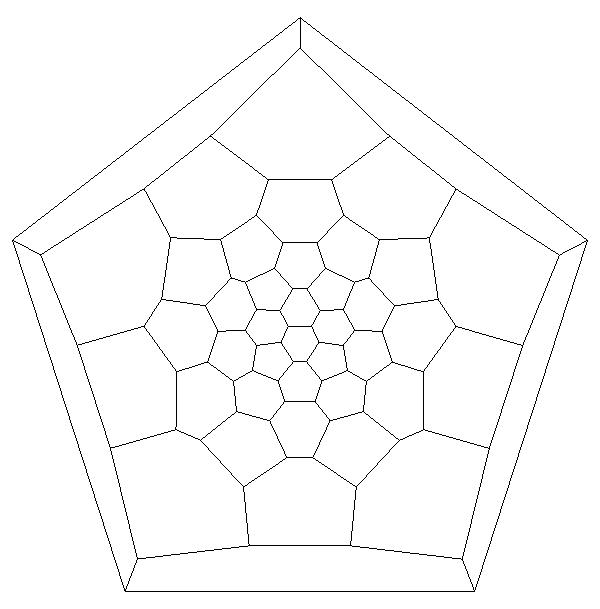
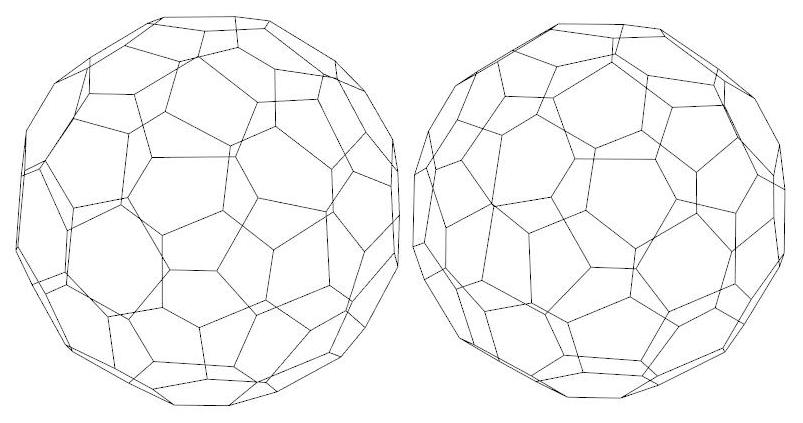
Schlegel
diagram of P44, centered on the back of the polyhedron.
In the near future, I plan to compute — and display here —
examples of nets,
for the benefit of those who prefer to use them for the
construction of models,
instead of using individual polygon templates.

Tetsuya Hatanaka and the P44 model
he assembled in Spring, 2011
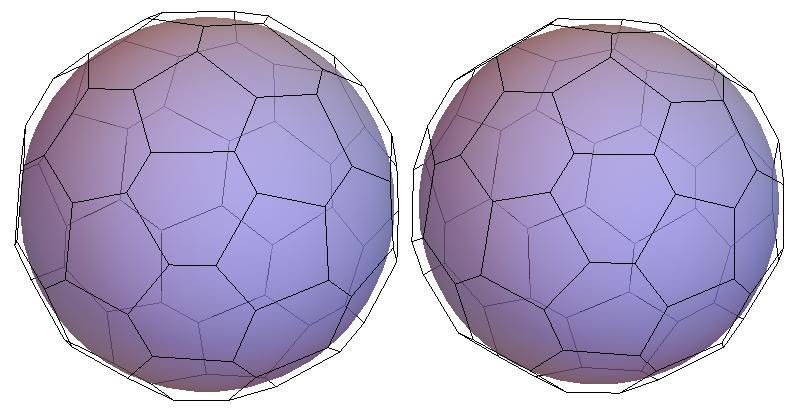
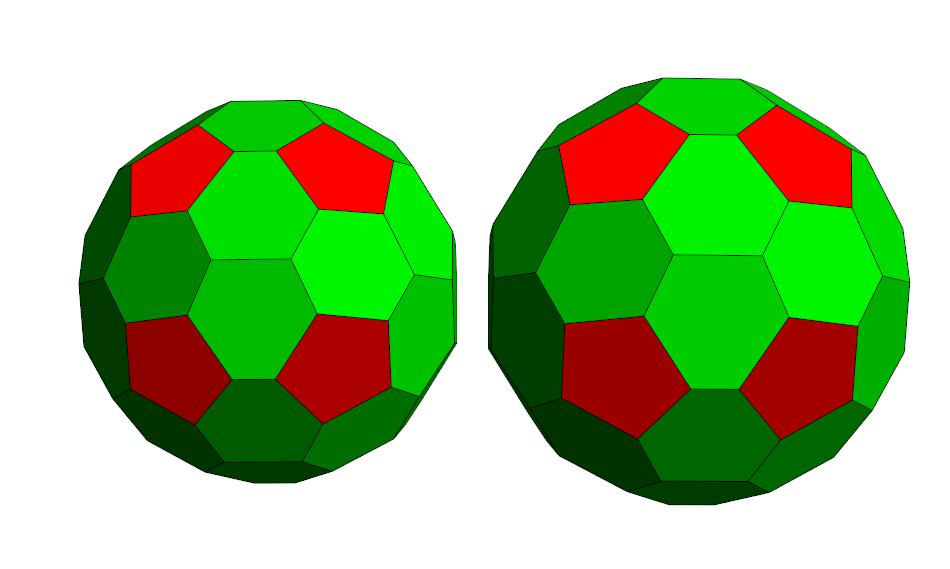
made in 1986. Below is a cross-eyed stereo pair of photos of this model.
Identifying its D2d symmetry required careful scrutiny of the model!


The model I constructed in 2011 of P44,
the putative 'roundest'
polyhedron with 44 faces (identfied in 1986).
Its symmetry is
D2d.
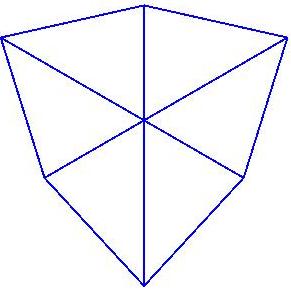
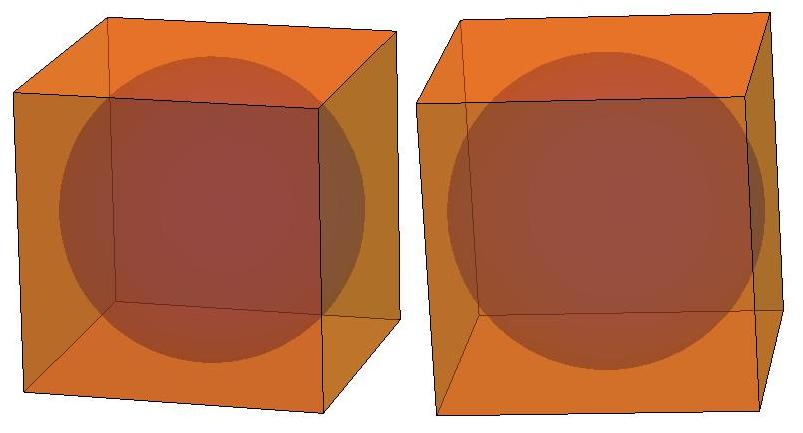
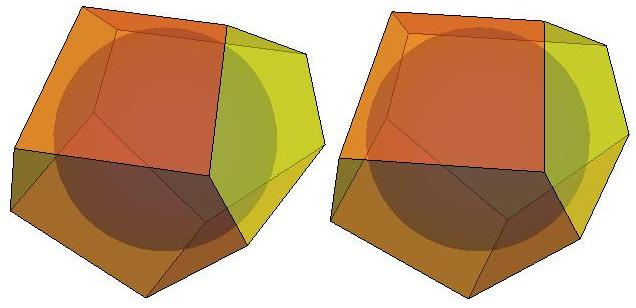
Below is a stereo image of a simpler convex
polyhedron with D2d
symmetry. It has the simplest possible combinatorial structure of all
convex polyhedra with D2d symmetry.
It is shown inscribed in a
cube of edge length
two. One of its two orthogonal c2 axes is the
blue line, which coincides
with the x-axis. The other c2 axis is the
red line,
which coincides
with the line between points at 0,1,1)
and (0,-1,-1).
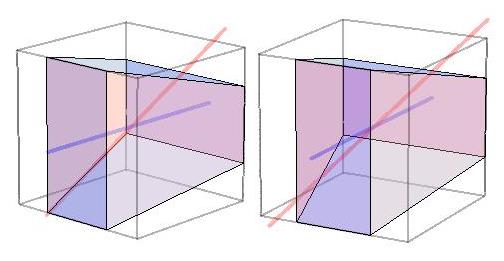
P44 also has two orthogonal planes of mirror symmetry, the horizontal
(equatorial) x-y plane
and the vertical x-z plane. It is invariant under two
successive rotations—a half-turn about the [vertical]
z-axis, followed by
a quarter-turn about the [horizontal] x-axis.
Like the convex hexahedron shown above,
if P44 is viewed from the
back, it appears the same as it does from the front,
except for the fact
that its image is rotated by a quarter-turn.
My 1986
conference paper
on roundest polyhedra lists only two other
values of n — 8 and 20 — for
which the roundest n-faced polyhedron
has D2d symmetry
(cf. pp. 162-164).
Although a separate template is provided here for each of the forty-four
faces of P44 (cf. above),
there are only eight different shapes of faces
—
two pentagons (p1 and p2) and
six hexagons (h1, h2,
...,
h6). The number
of specimens and the symmetry of each face are given below.
Each of the
asymmetrical face shapes occurs in two four-specimen subsets. The faces in
one of these subsets are reflected images of the faces in the other subset.
pentagons
4 p1: d2 symmetry
8 p2: c1 symmetry (i.e. asymmetric)
hexagons
4 h1: d2 symmetry
4 h2: d2 symmetry
4 h3: d2 symmetry
4 h4: d2 symmetry
8 h5: c1 symmetry
8 h6: c1 symmetry
The results described in my 1986
conference paper
and in the May 1986
supplement
demonstrate that roundest polyhedra exhibit a great variety
of
symmetries.
Determining the symmetry of each of these polyhedra is
an interesting challenge.
It is probably best accomplished by examining,
from different directions, either physical models
or — more simply! —
virtual models, using a computer program like
Mathematica, for example.
In 1989, my student David M. Aubertin wrote a
computer science masters thesis
in which he designed and implemented a program for
obtaining and displaying
solutions for the
4-dimensional version of
the isoperimetric problem for polyhedra.
Here is a hyperlink to his thesis, which is entitled
'Optimization of Four-Dimensional Polytopes'.
It contains numerous stereoscopic
perspective drawings of projections
into R3 of the
solution 4-polytopes. It also
includes a listing of the elegantly structured FORTRAN
program Dave wrote
for this study, together with a short BASIC program for
displaying the perspective images.
He has informed me that you are quite welcome
to copy and run these programs.


Photographed by Reiko Takasawa Schoen on October 20, 2012
at the New York City Metropolitan Musem of Art
Below are a few examples of Schlegel diagrams of sphere-inscribed
polyhedra of maximum volume for a given number of vertices. I
constructed all except for the simplest of these Schlegel diagrams from
polyhedron vertex data generously shared with me by Wayne Deeter.
n=4
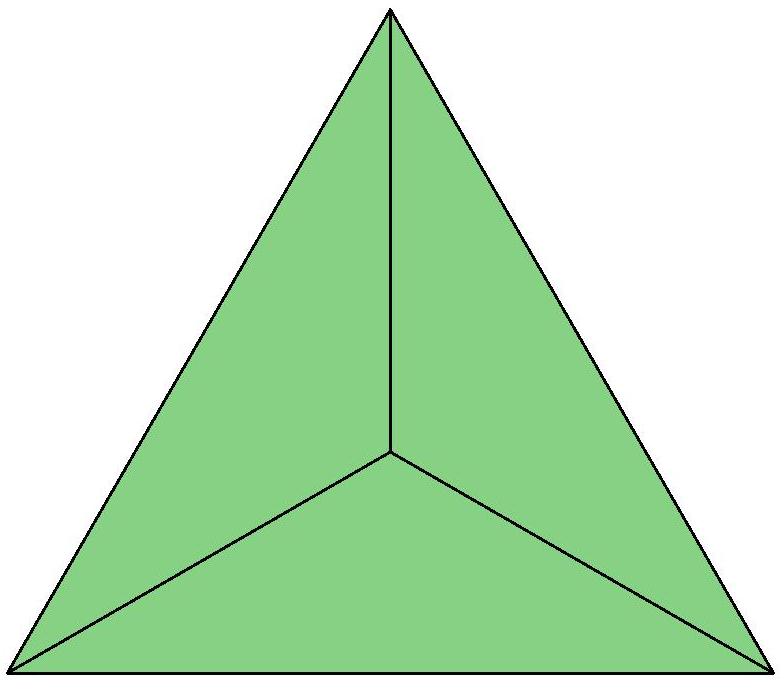


n=5


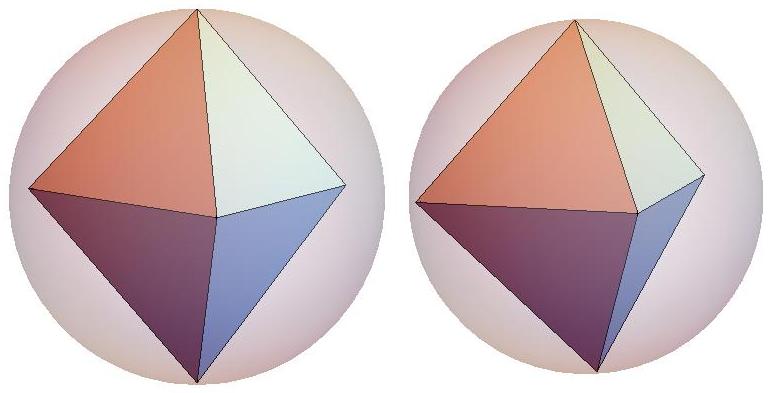
n=6
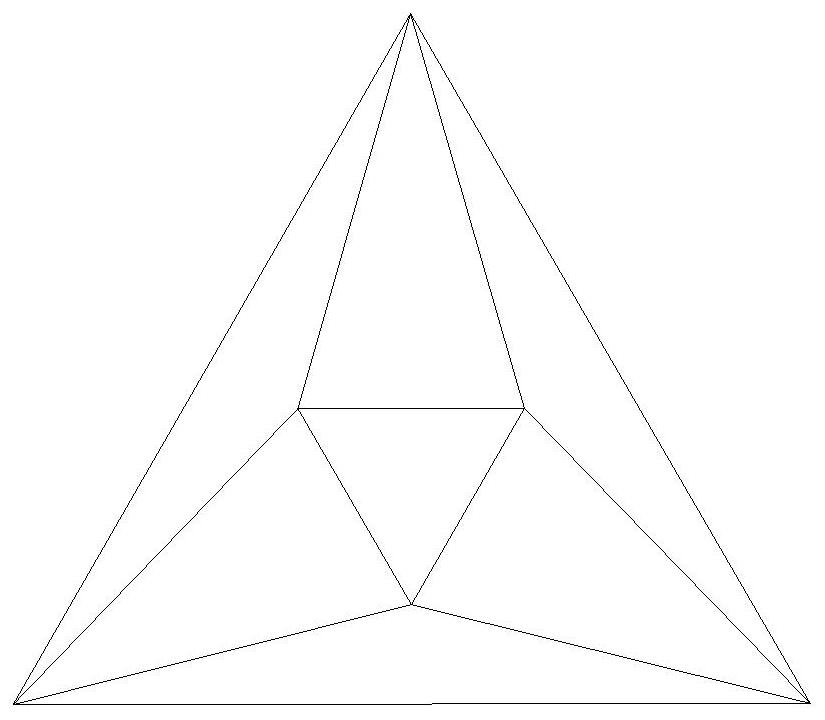

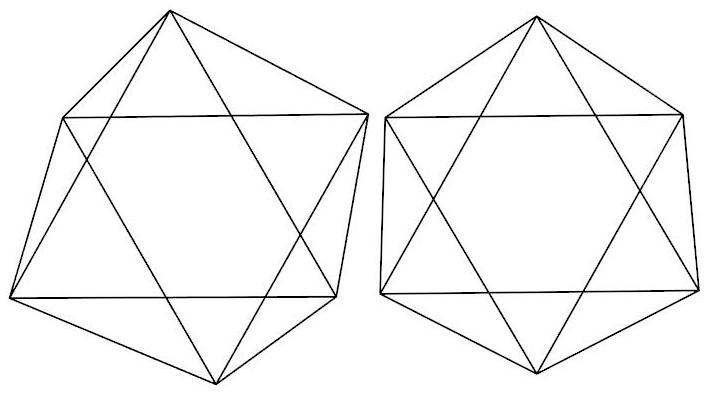
n=7
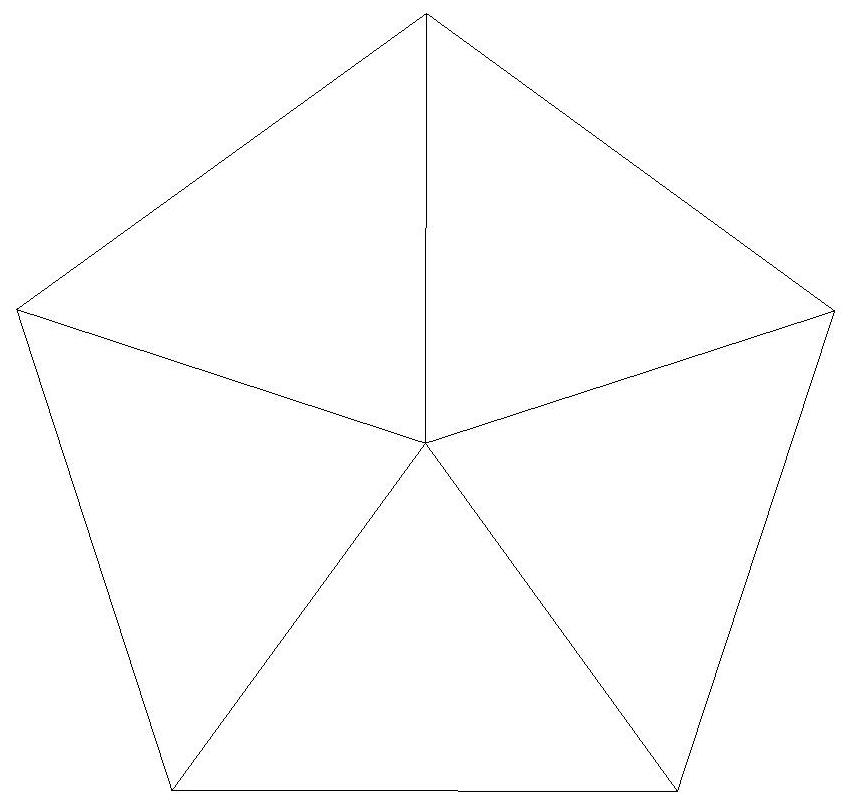




n=8
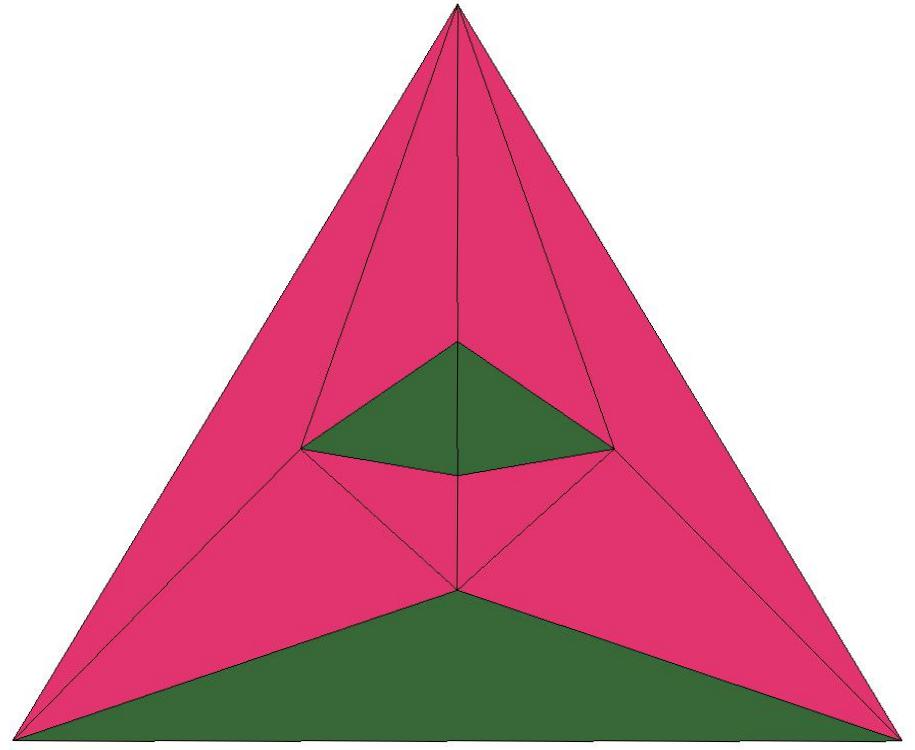
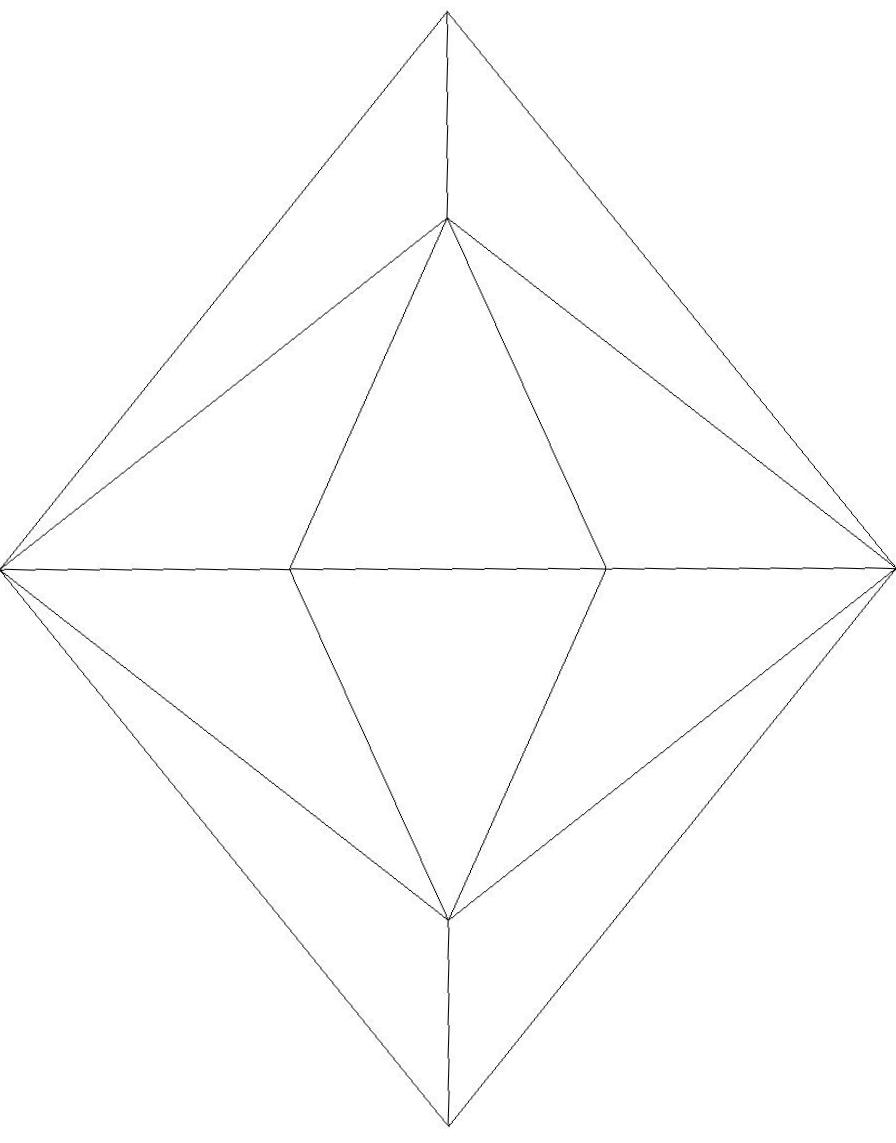



n=9
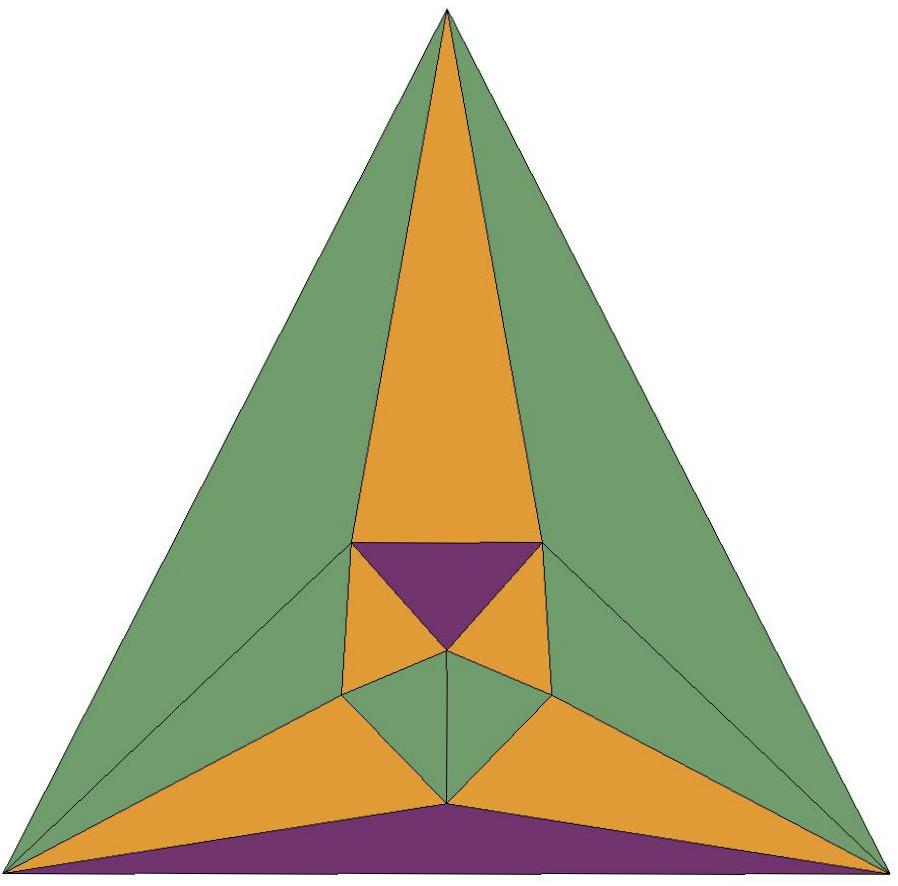
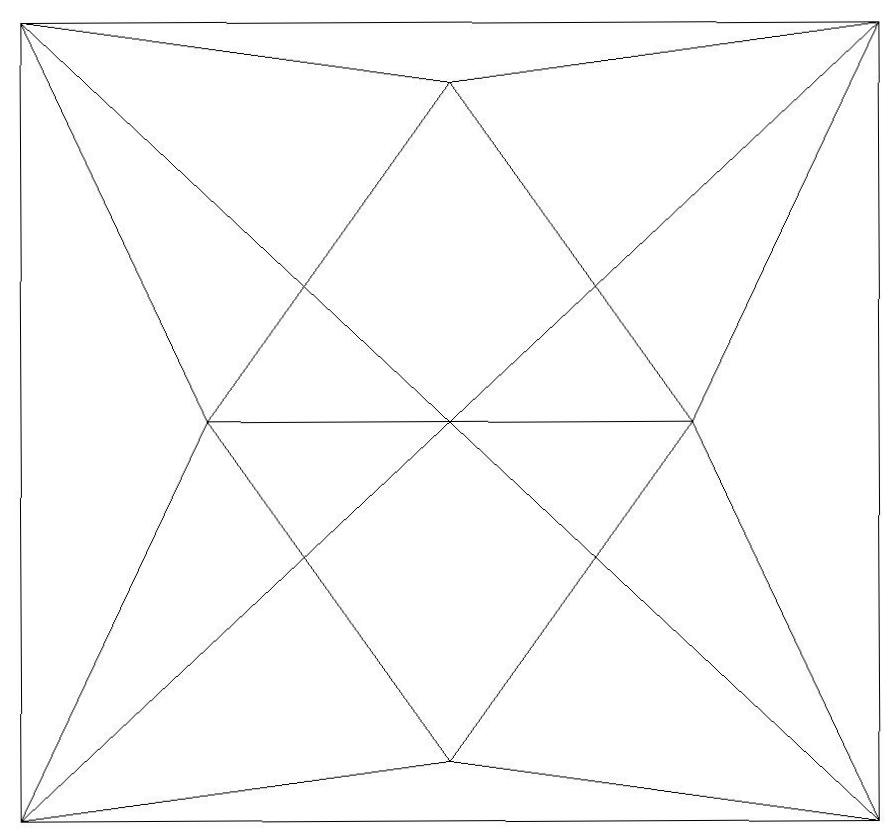


n=10
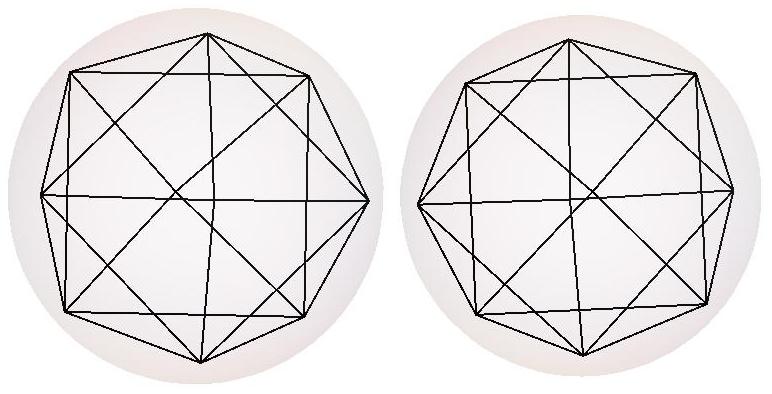



n=11
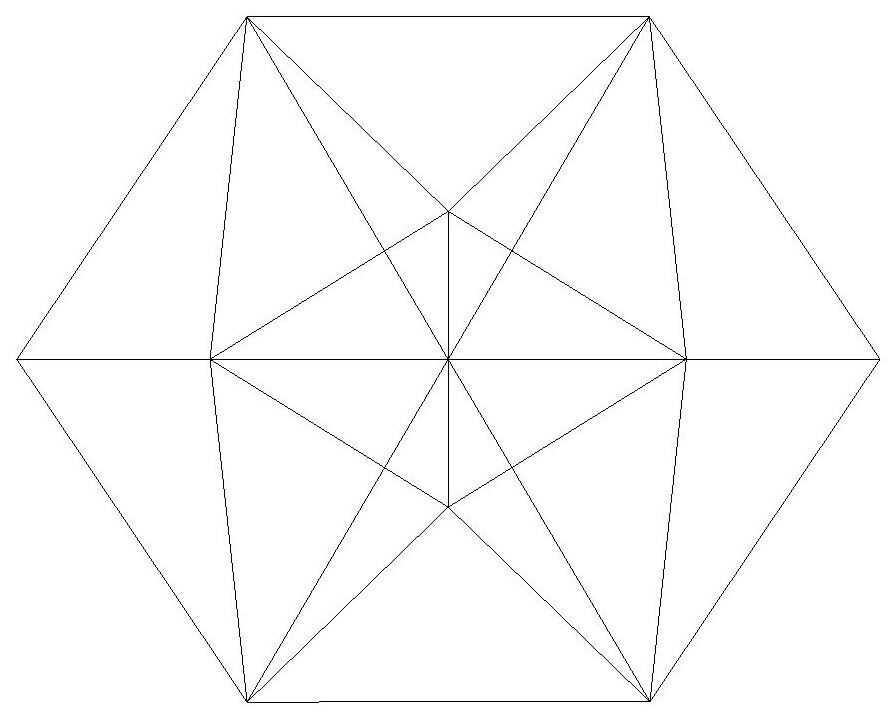


n=12
.jpg)


n=13
.jpg)
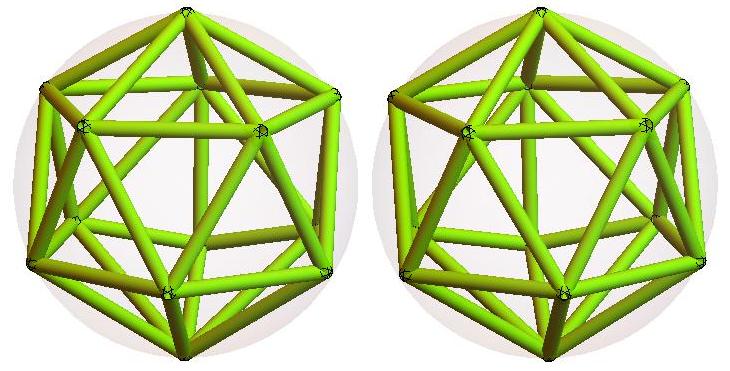
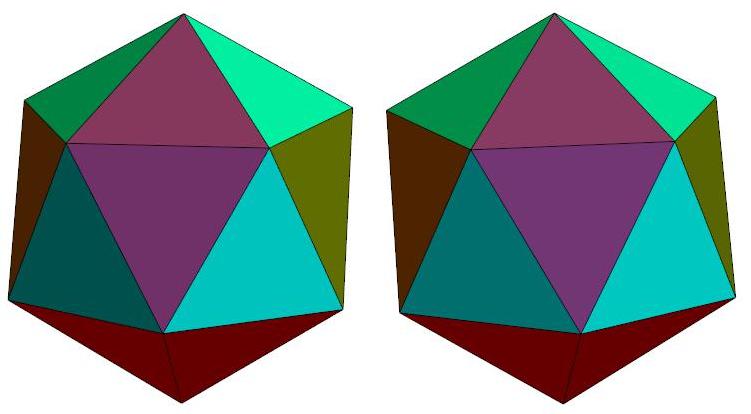
n=14
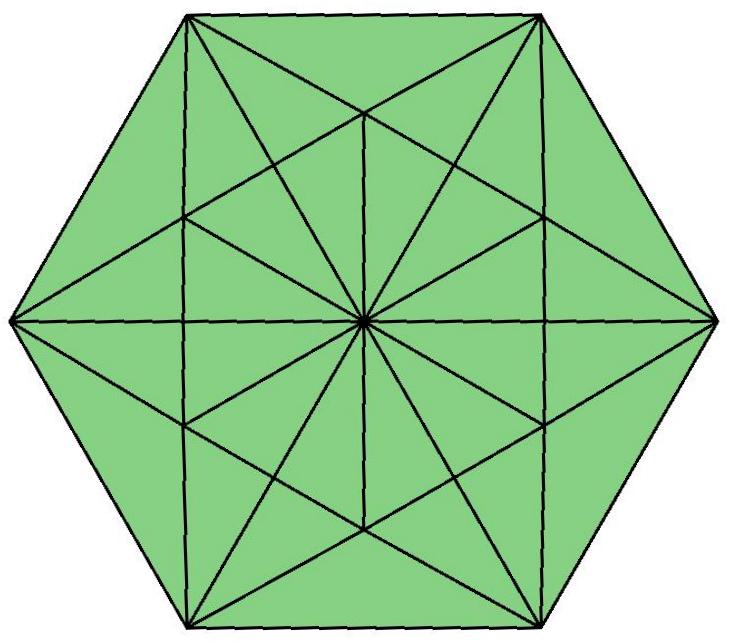


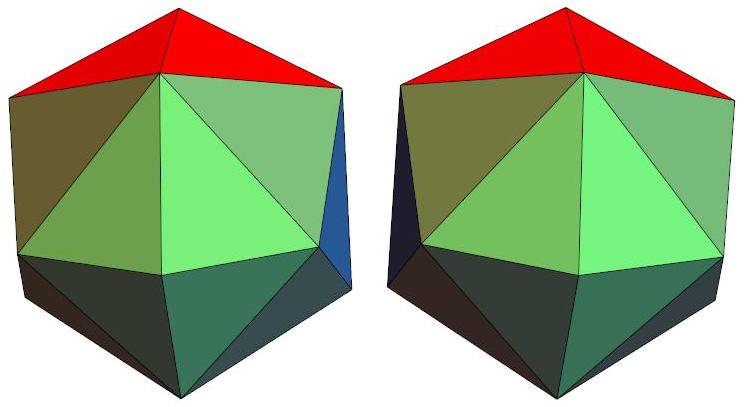
n=15
n=16
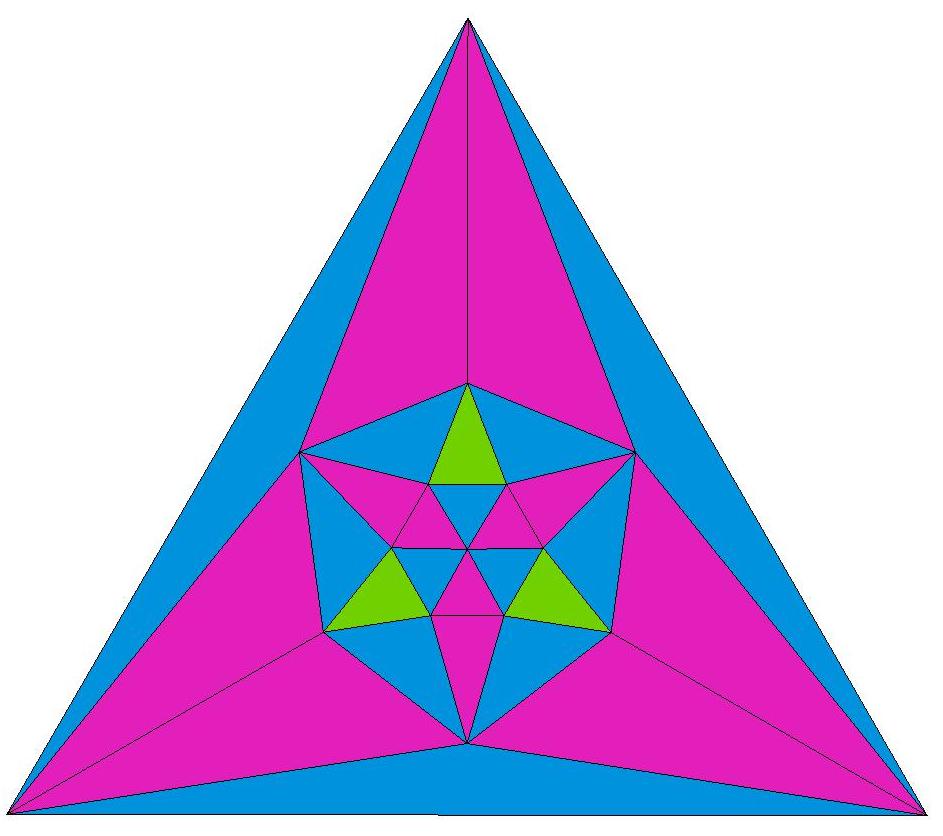

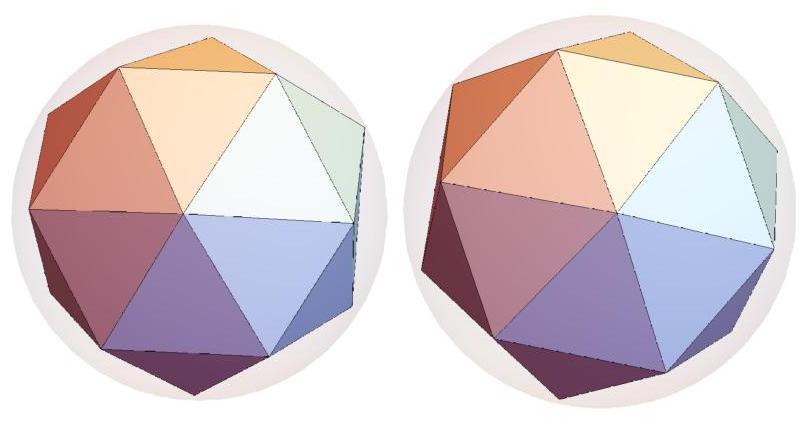
n=17
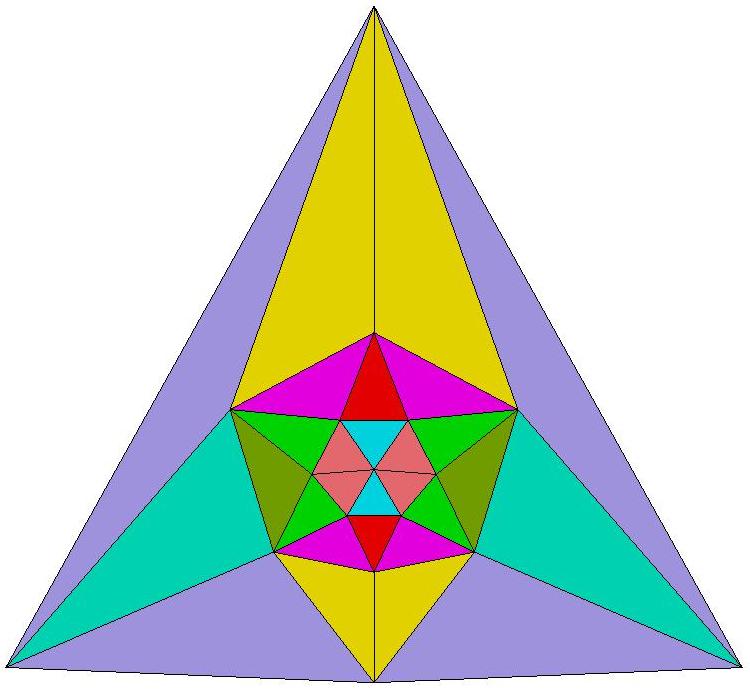

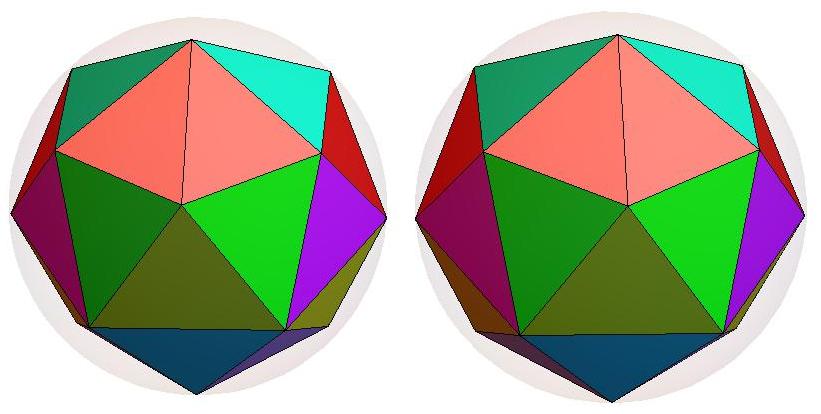
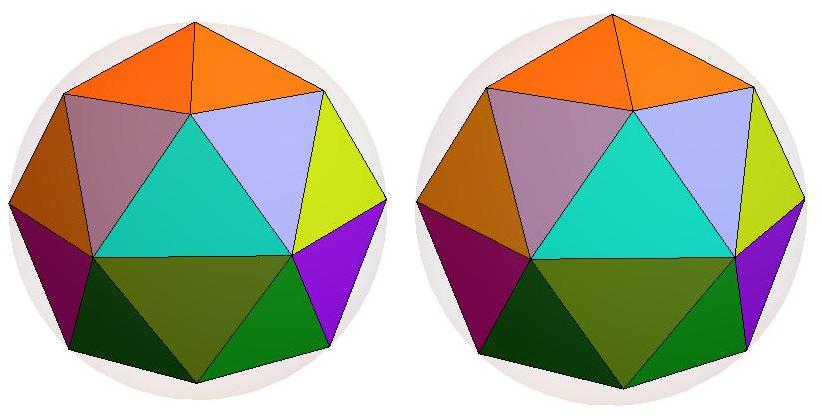
n=18

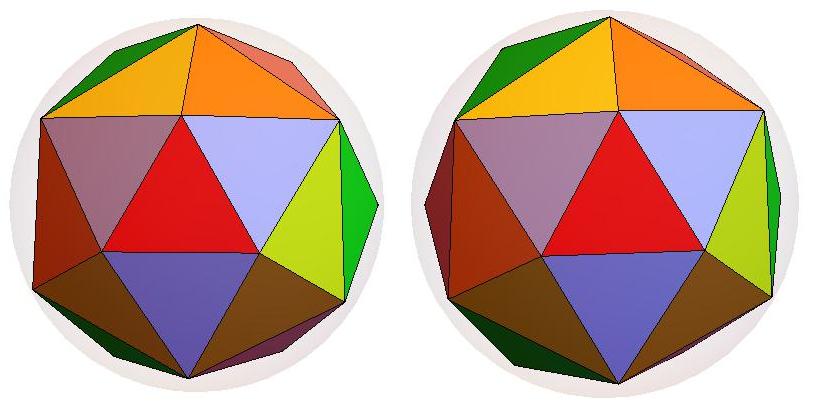
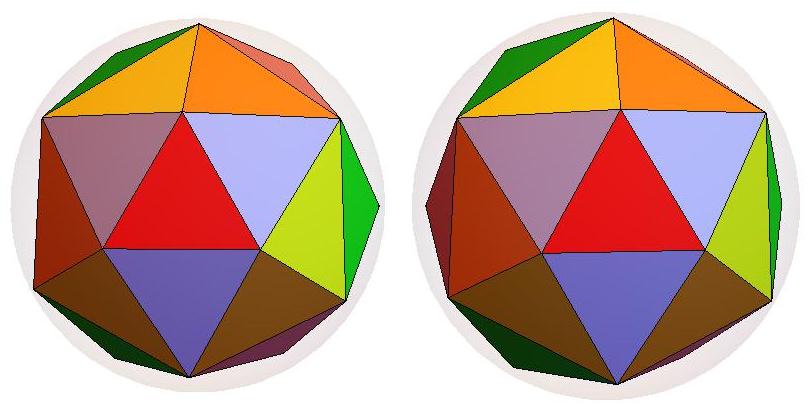
n=19
.jpg)

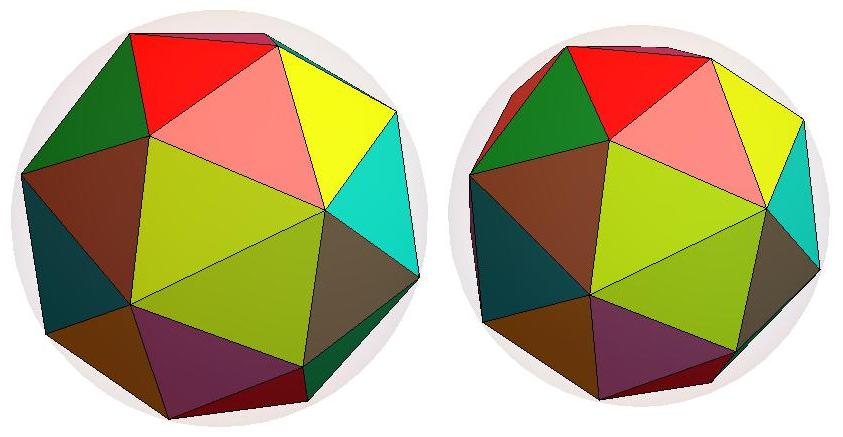
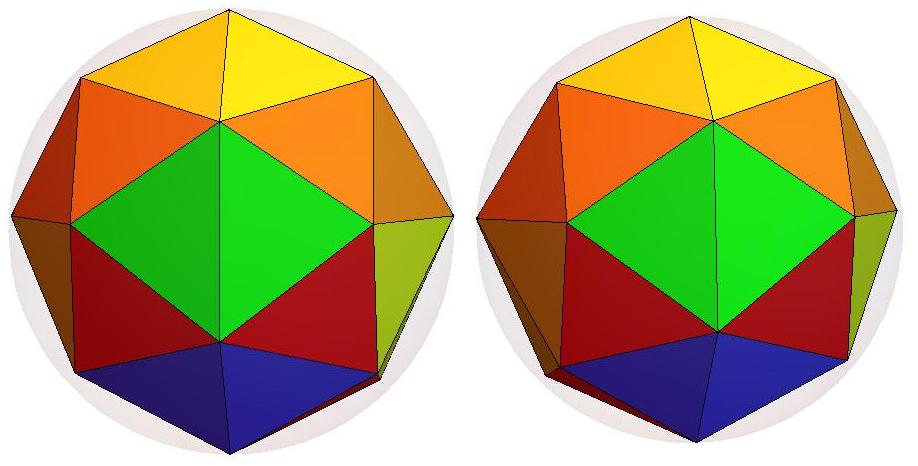
n=20
.jpg)
.jpg)
.jpg)
.jpg)

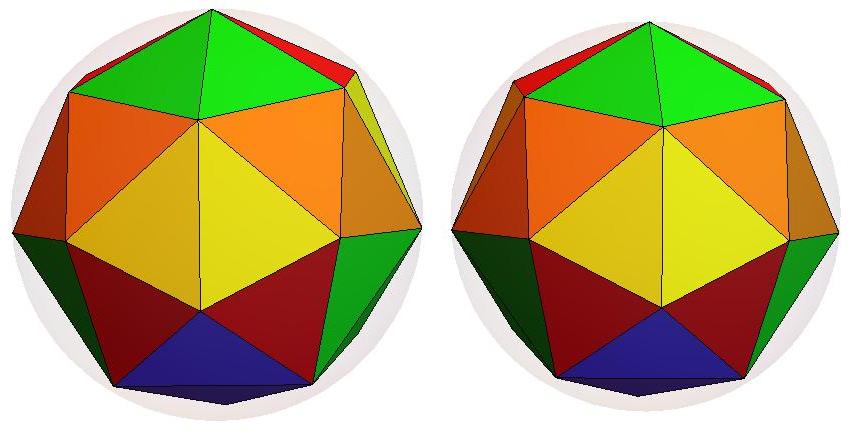
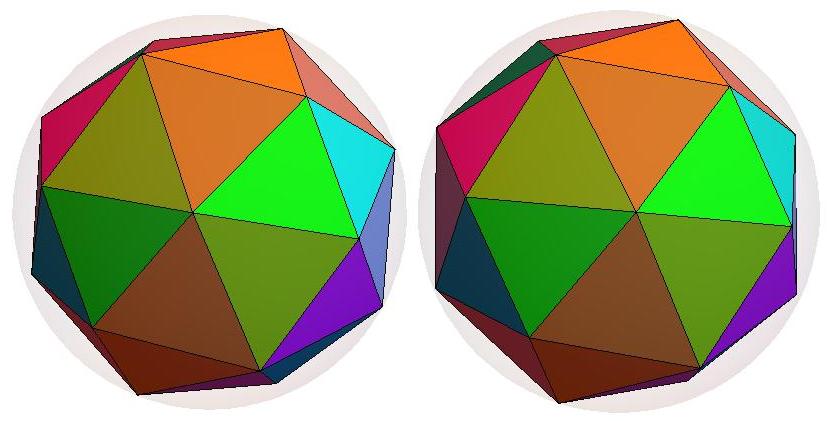
n=21
.jpg)

.jpg)
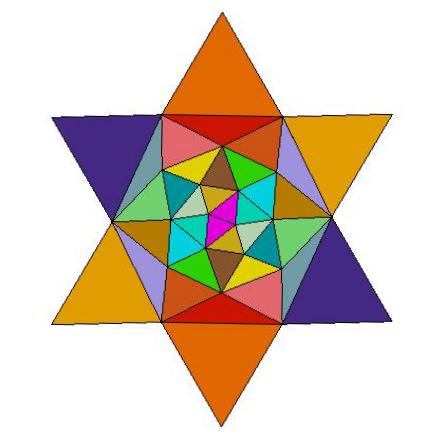
n=22
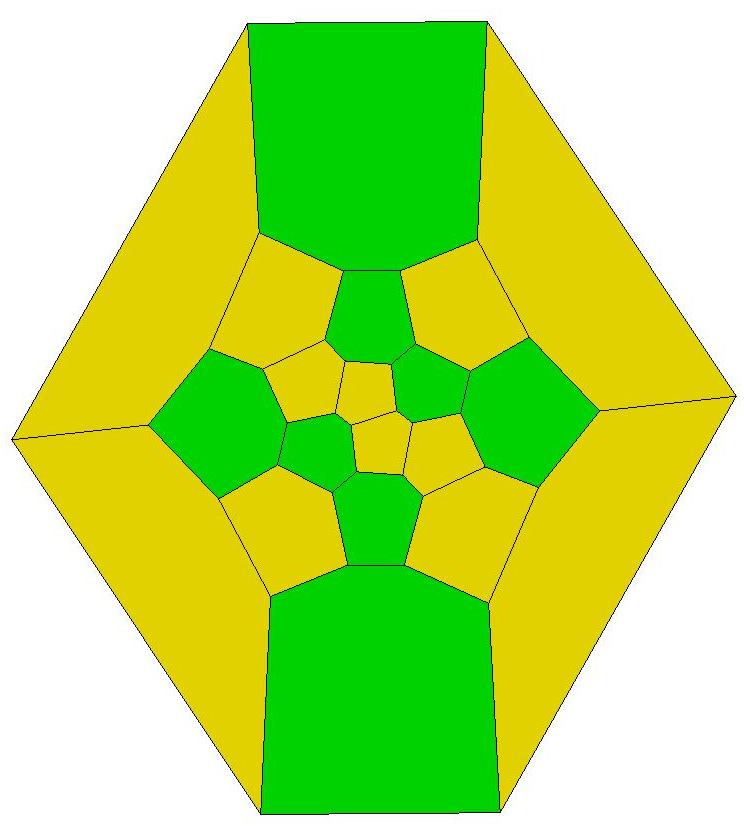
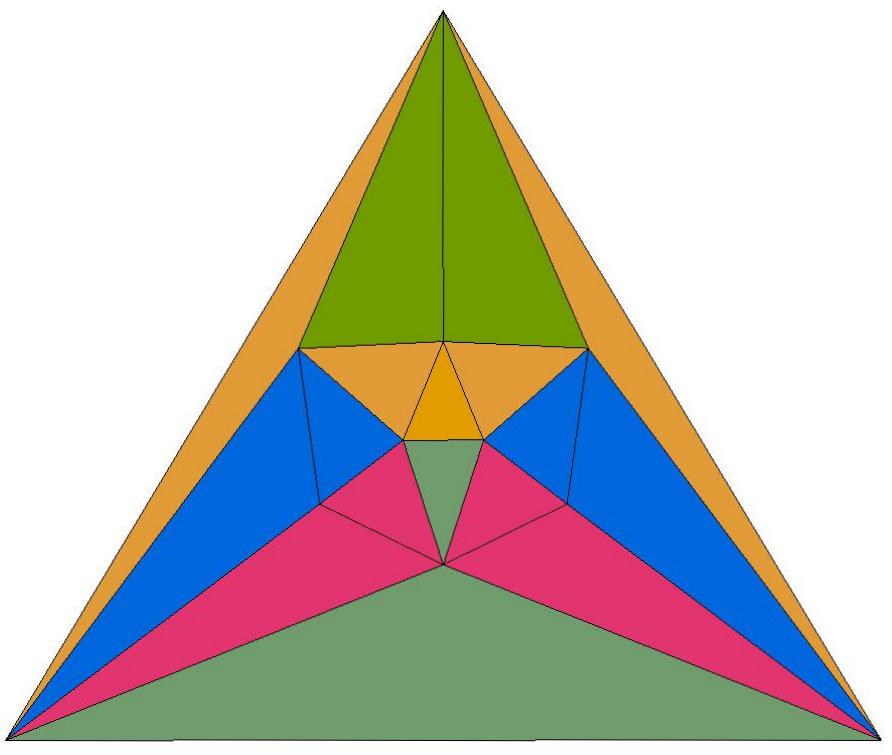
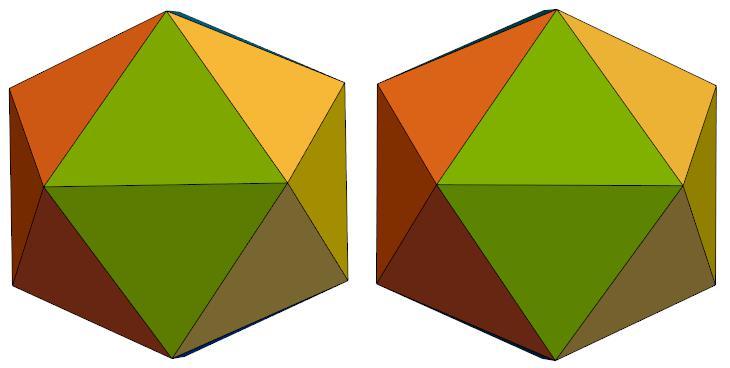
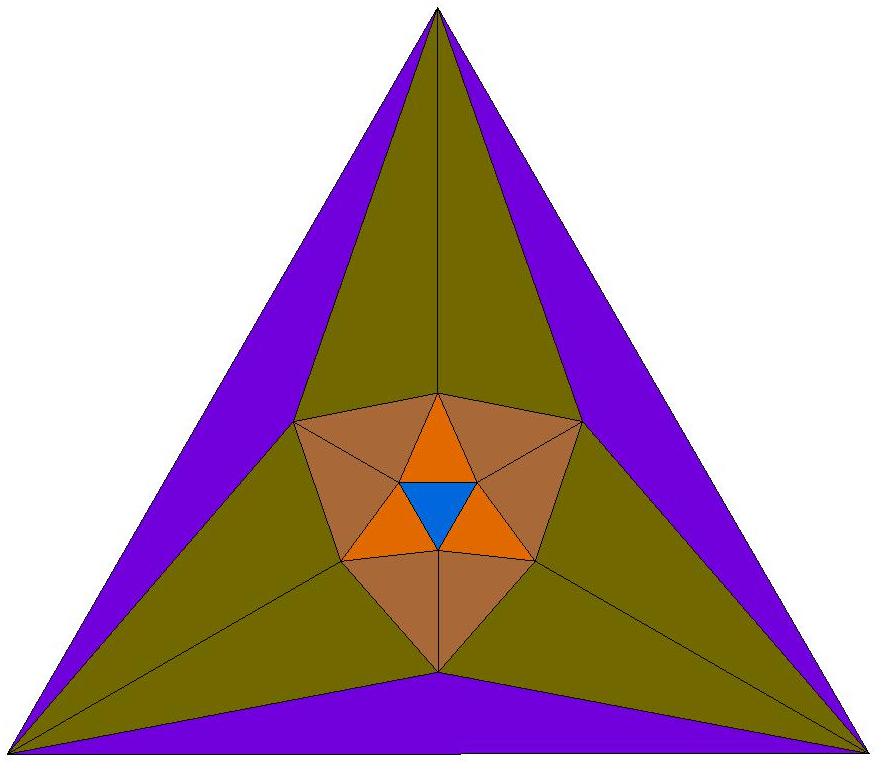
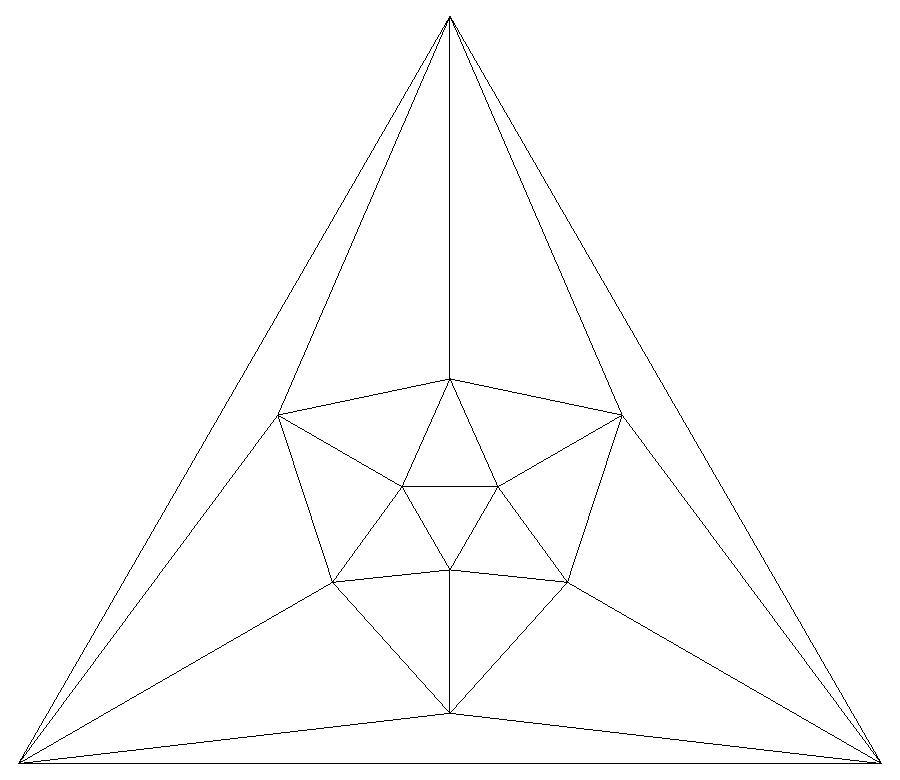
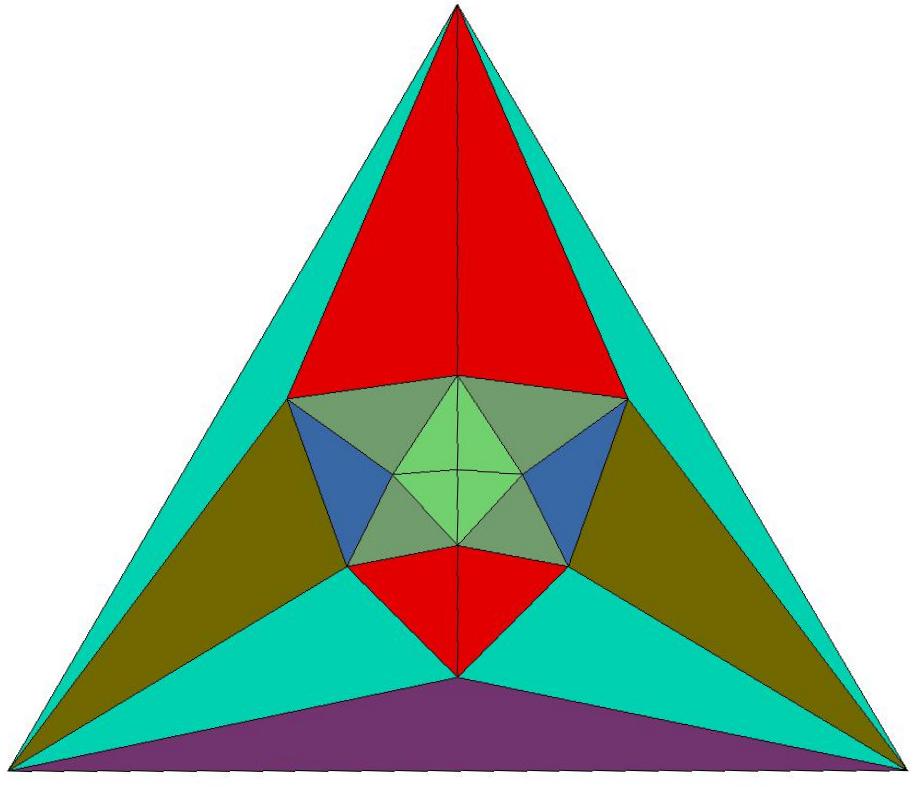
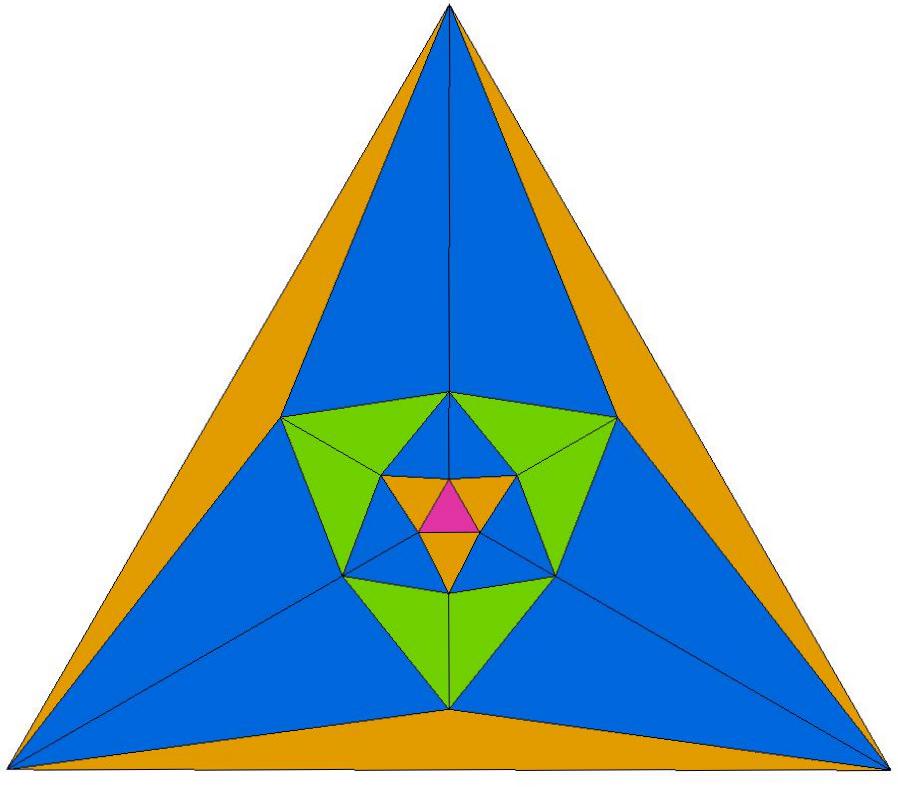
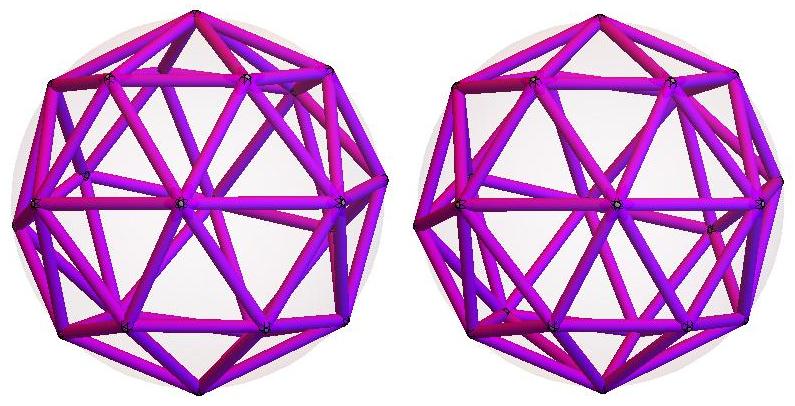
Q22 is composed of 40 triangles of 10 distinct shapes.
There are 4 specimens of each shape.
.jpg)
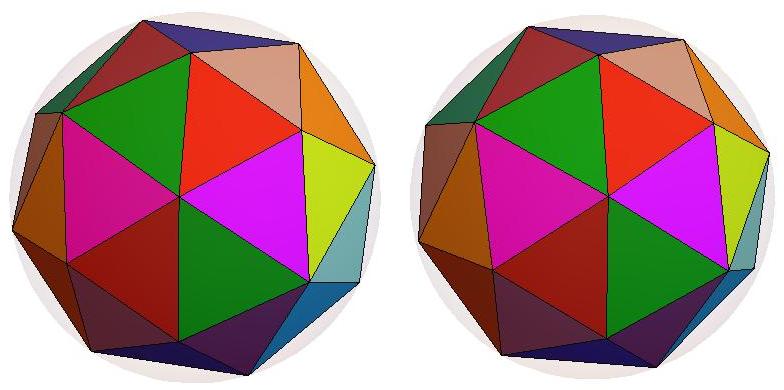
front view
rear view
wireframe
Schlegel diagram of a 36-face subset of Q22
viewed along a diad axis
Star-like Schlegel diagram of Q22
viewed along a diad axis
.jpg)
Schlegel diagram of Q22
viewed along a 'quasi-diad axis'
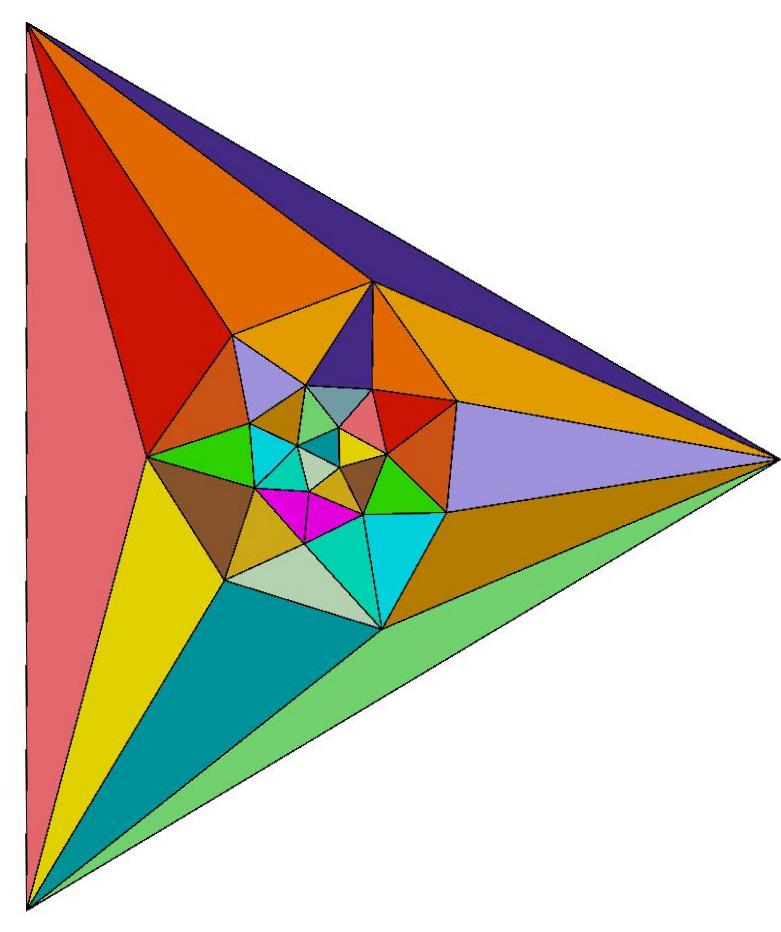
n=23
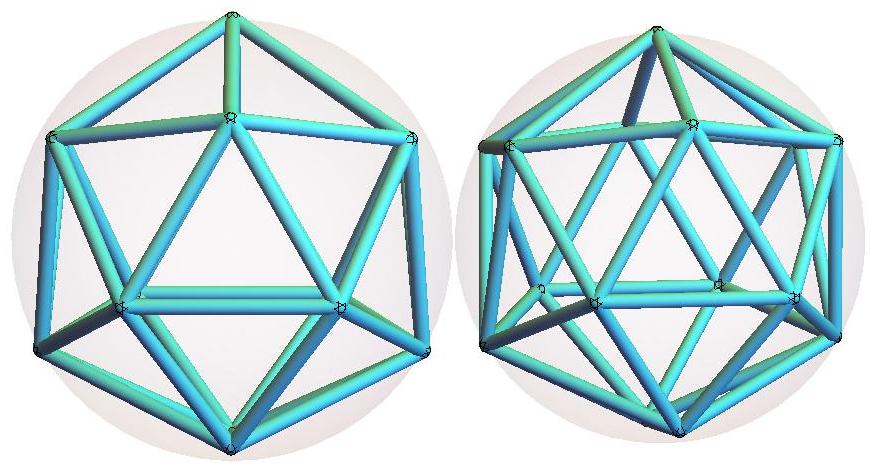
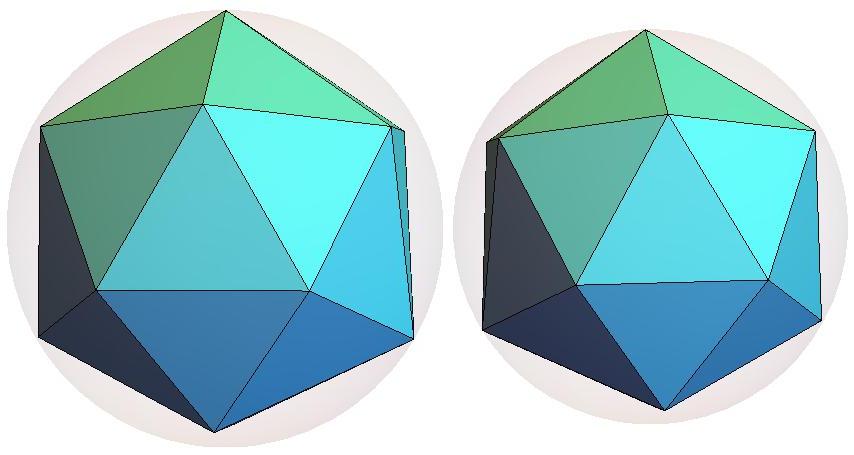
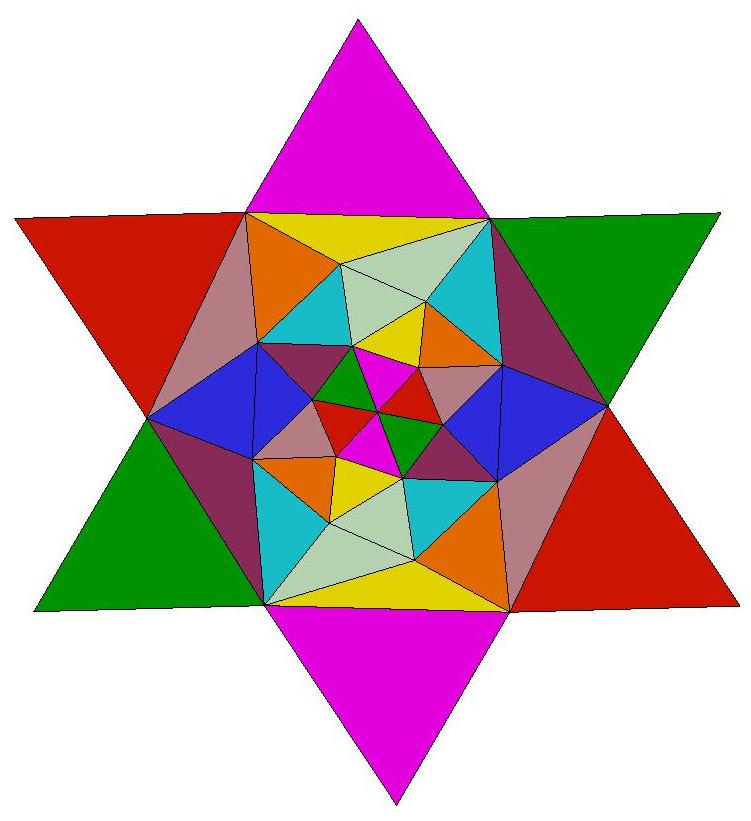
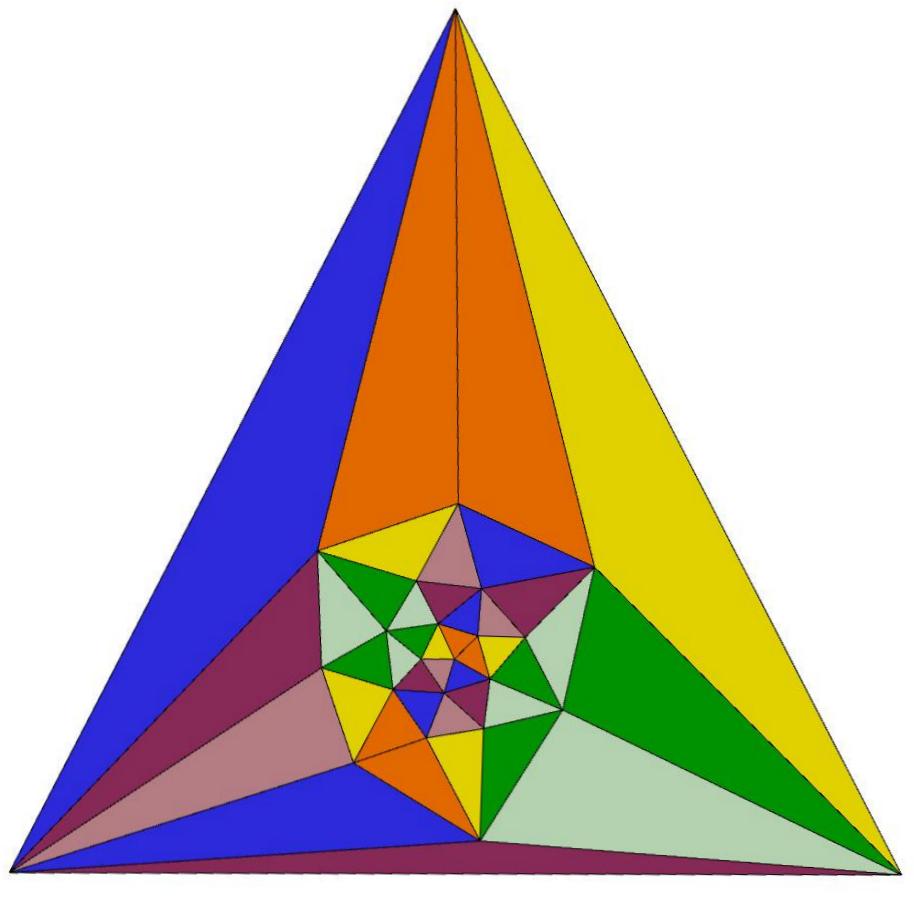
Q23 is composed of 42 triangles of 7 distinct shapes.
There are 6 specimens of each shape,
coded by color in the image below.
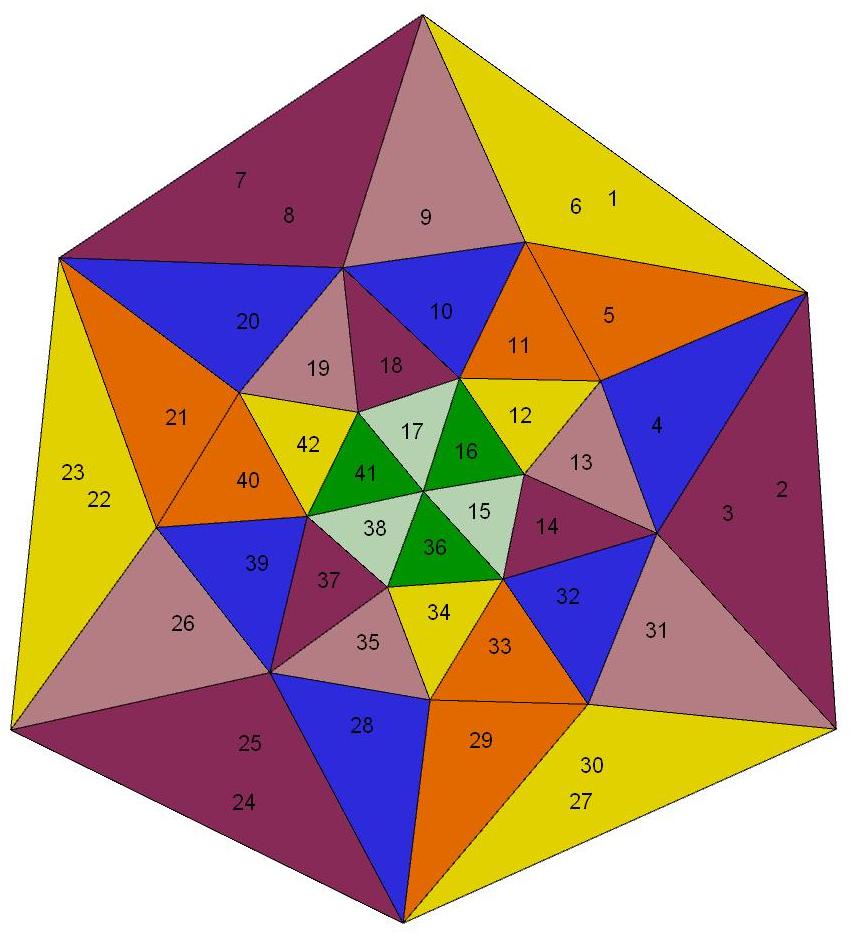
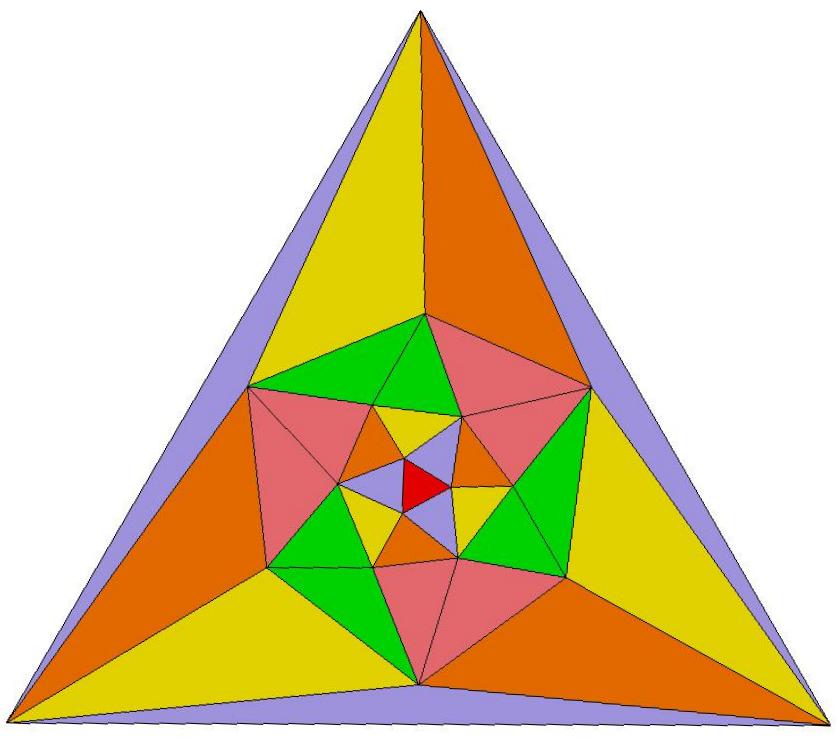
c3-symmetric Schlegel diagram of
a 36-face subset of the 42 faces of Q23

Symmetrical Schlegel diagram of S23(2),
a second 36-face subset of the 42 faces of Q23

c3-symmetric star-like Schlegel diagram of Q23



front view
rear view
wireframe
.jpg)
Q42
n=72
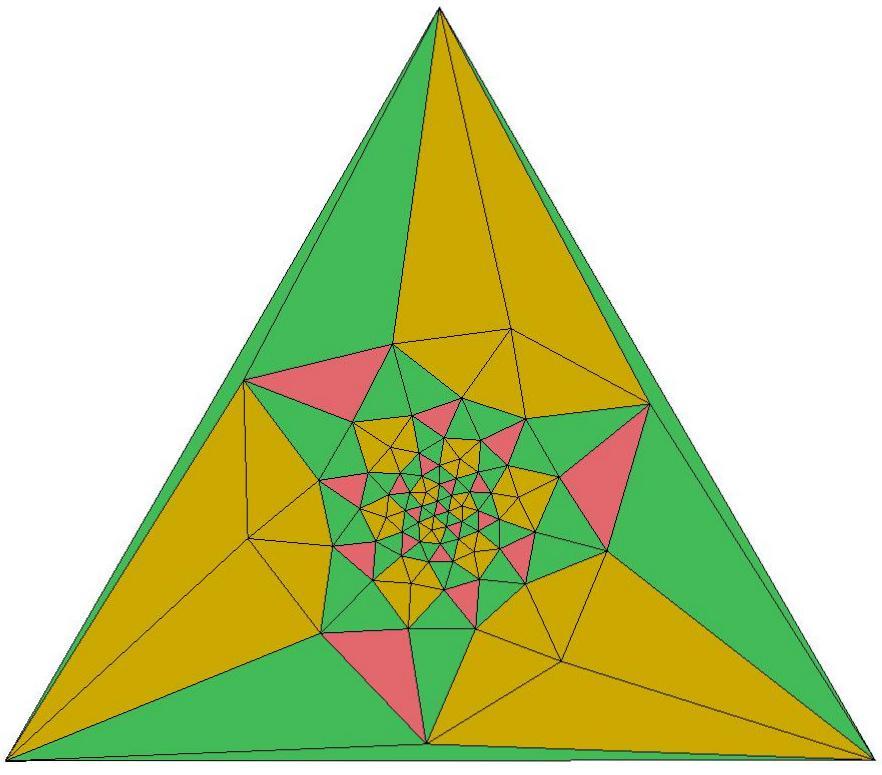
c3-symmetric Schlegel diagram of Q72
no. of pink faces = 20
no. of gold faces = 60
no. of green faces = 60
f = no. of faces = 140
e = no. of edges = 3f /2
= 210
v = no. of vertices
Euler's equation:
v - e + f = 2
Hence v = e - f + 2
= 72
.jpg)
c3-symmetric Schlegel diagram of Q72
.jpg)
c2-symmetric Schlegel diagram of Q72
.jpg)
c2-symmetric Schlegel diagram of Q72
n=122
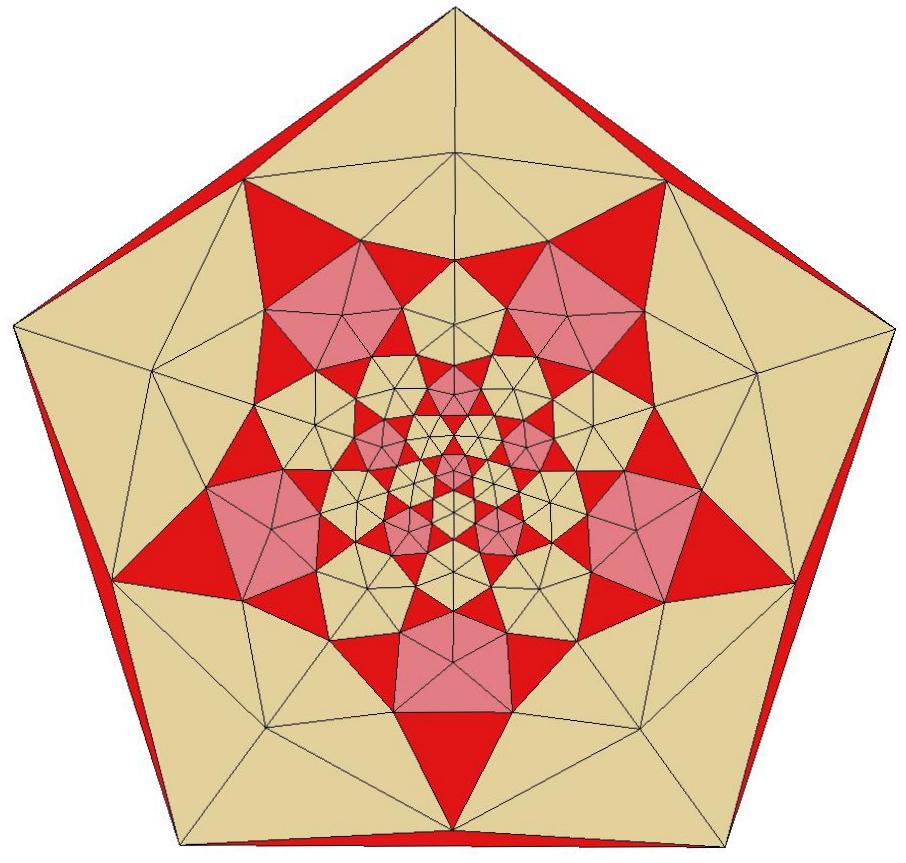
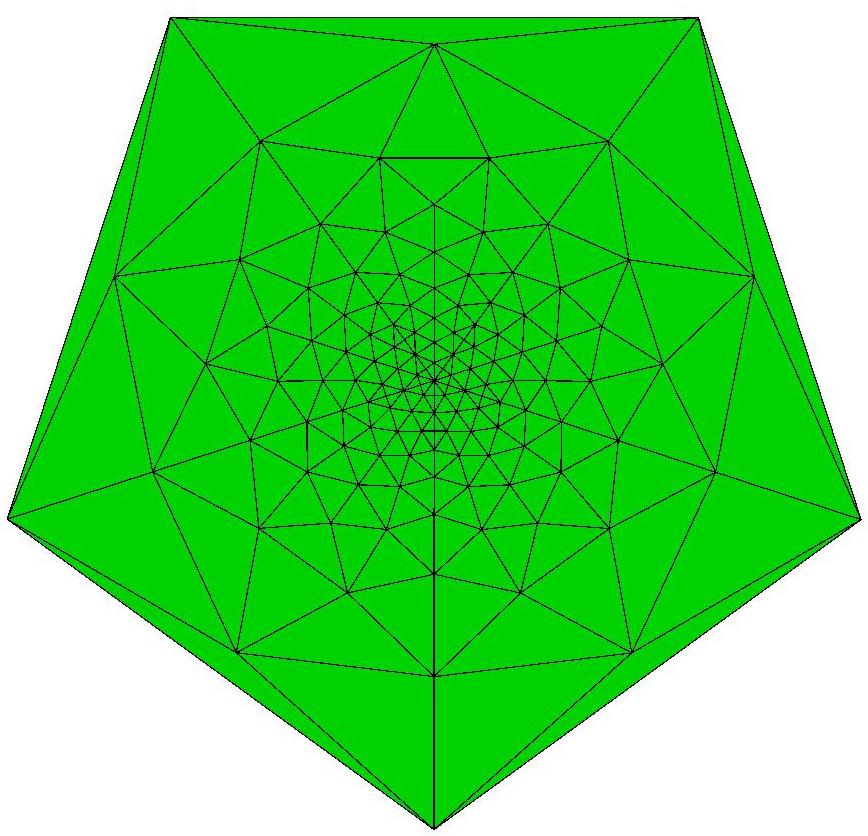
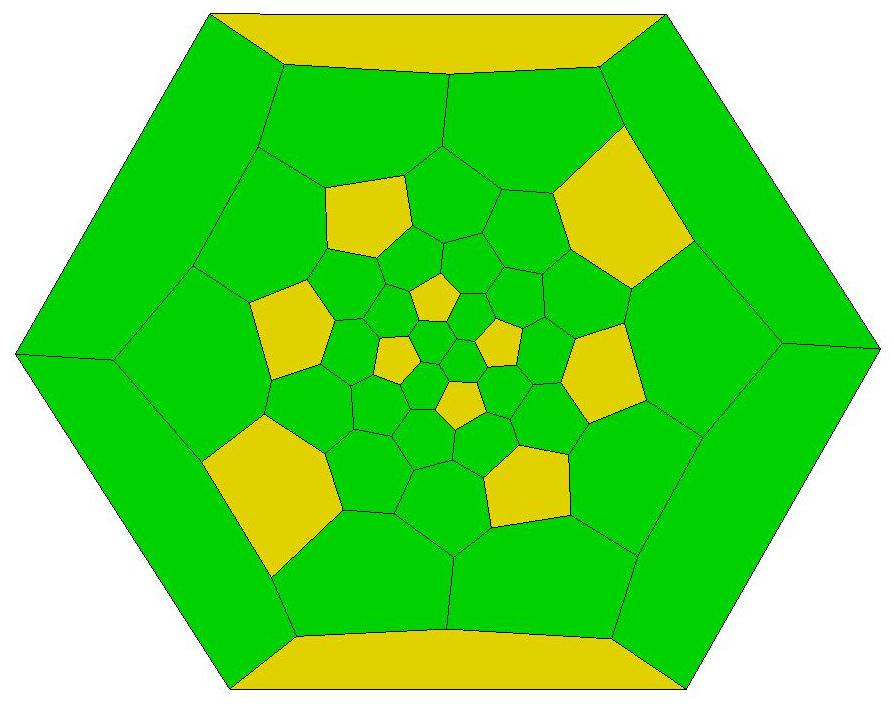
Schlegel diagram of a 235-face subset of the 240 triangular
faces of Q122,
which is the dual of a
Goldberg polyhedron.
Q122 is composed of 240 triangles of 3 distinct shapes. It is
composed of 60 specimens each of both the largest and smallest
triangles and 120 specimens of the triangle of intermediate size.
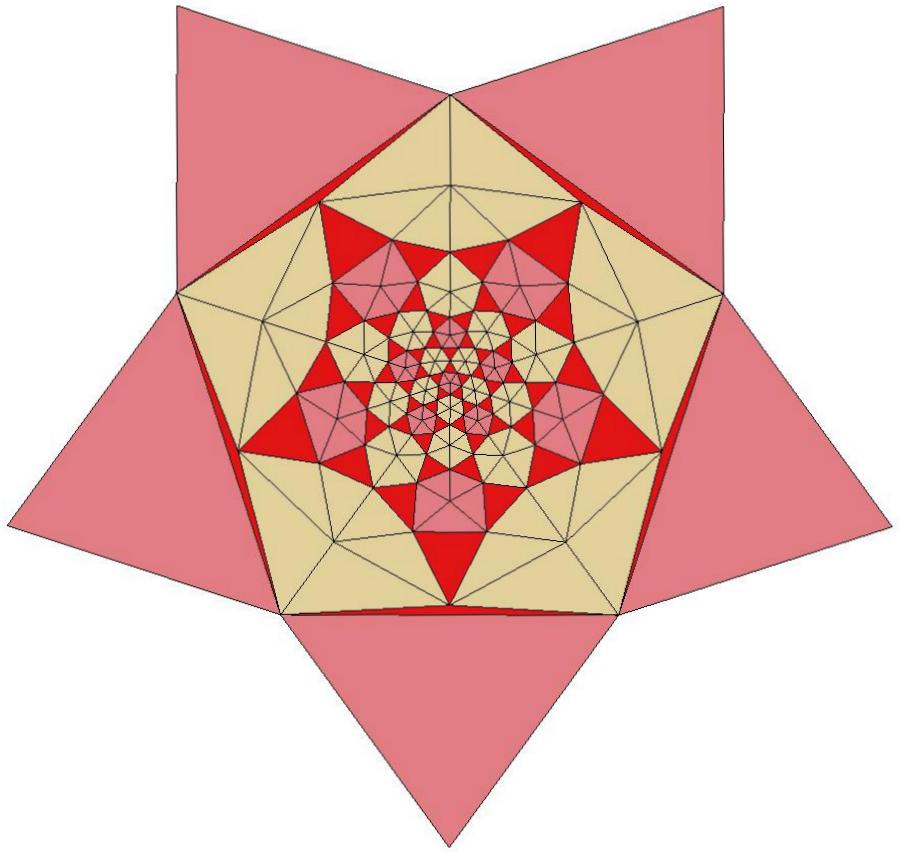
Star-like Schlegel diagram of Q122. It includes the
five faces omitted from the diagram shown just above.
(Click here for a higher resolution image.)

Q122
no. of pink faces = 60
no. of red faces = 60
no. of yellow faces = 120
f = no. of faces = 240
e = no. of edges = 3f /2
= 360
v = no. of vertices
Euler's equation:
v - e + f = 2
Hence v = e - f + 2
= 122
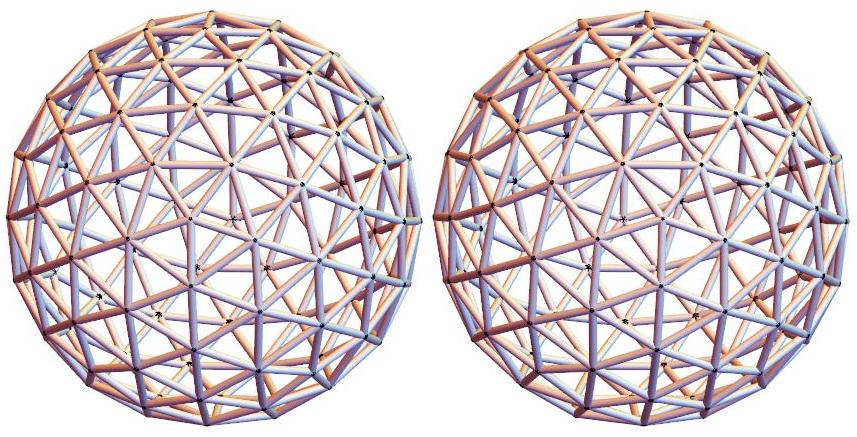
Q122 wireframe
.jpg)
c2-symmetric Schlegel diagram of Q130