Back to GEOMETRY GARRET

Alan H. Schoen

Comments are welcome!

Support Wikipedia

Locations of visitors to this page


Hibiscus blossoms on our front porch
(Summer, 2011)


B. FINITE TILINGS BY RHOMBS

The lowly rhomb — a parallelogram with sides of equal length — has acquired special notoriety during the past few decades as the shape of the two prototiles of Penrose patterns. But there are several other kinds of tiling patterns by rhombs in which the rules that govern tile placement, though less subtle than the rules for Penrose tilings, are nevertheless sufficiently non-obvious to require some analysis. Some of these other kinds of tilings, both finite and infinite, are discussed below.

But first— a frivolous design:

A SELF-SIMILAR TILING
COMPOSED OF SIX NESTED RINGS OF RHOMBS

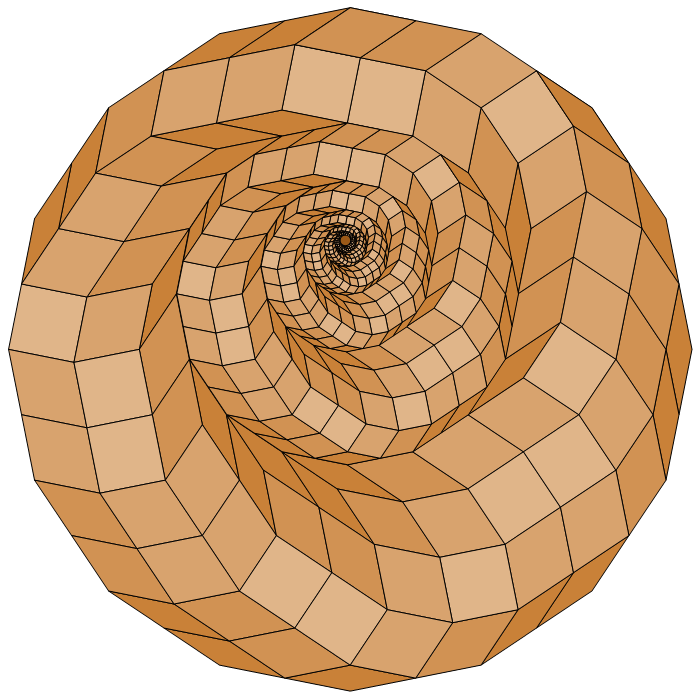
This arrangement of eccentrically nested rings is not an edge-to-edge tiling (cf. p.18 of Tilings and Patterns, by Grünbaum and Shephard). From now on, all the tilings considered here are of edge-to-edge type.


B1. ROSETTES (and PSEUDO-ROSETTES)

A rosette is an example of a finite tiling by rhombs. In § C1, C2, and C3, I consider a different kind of finite tiling by rhombs—the finite core of an infinite recursive tiling. A major difference between these two types of tiling is that while the number of rhombs of each shape in a rosette is fixed by the choice of the positive integer n, the number of rhombs of each shape in the core of an infinite recursive tiling is not restricted, because there is no upper bound on the size of the core.

I define a simple rosette as any edge-to-edge tiling by rhombs of a regular convex polygon with an even number 2n of sides; n is called the order of the rosette. The sides are defined to be of unit length. A square is a rosette of order two. The number m of rhombs in a rosette increases quadratically with n (m = n (n − 1) ⁄ 2), and this increase is accompanied by a combinatorial explosion in the number of ways the rhombs can be arranged. Of particular interest are symmetrical rosettes. When n >> 2, it is not immediately obvious what rules govern their structure. I explore this question below.

First, however, let's examine how to use straight edge and compass to draw a particular class of tilings I'll call compound rosettes. My seventh-grade classmates and I learned this trick in 1936 from Miss Beatrice Wild, our art teacher in Room 314 of William Wilson Jr. School in Mount Vernon, N.Y.

The first step is to inscribe 2n unit circles (n = 2, 3, 4, …) inside — and tangent to — a circle of radius 2. The unit circles are spaced uniformly along the circle boundary.

The second step is to join by line segments certain pairs of points where circles — whether small or large — intersect in non-overlapping four-point cycles that define rhombs. The rhombs inside each unit circle define a simple rosette I'll call the STRAWBERRY. Since the unit circles overlap, the STRAWBERRIES do too (except in the case n = 2). Examples of compound rosettes for n = 2, 3, and 4 are shown below.


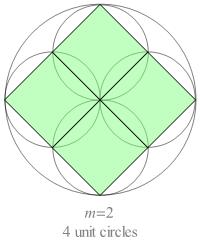
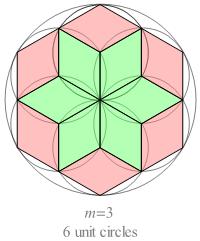
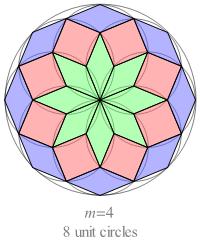
Fig. B1.1
Compound rosettes for n = 2, 3, and 4

From now on, unless stated otherwise, every rosette will be assumed to be simple.

Some vital statistics:
For n = 2:
        There is a single rhomb — the square.
For odd n:
        There are (n − 1) ⁄ 2 different shapes of rhomb, with smaller face angles equal to kπ/n (k = 1, 2, ..., (n − 1)/2), respectively.
For even n ≥ 4:
        In addition to n ⁄ 2 specimens of the square, there are n specimens of each non-square rhomb, with smaller face angles equal to kπ ⁄ n (k = 1, 2, …, n ⁄ 2), respectively.

There are altogether n(n − 1) ⁄ 2 rhombs in every rosette. They comprise what I call the Standard Rhombic Inventory of order n, or SRIn.

For rosettes of order n > 4, the n(n − 1)/2 rhombs in SRIn can be arranged to form a variety of different rosettes. For n = 5, for example, there are six different arrangements:

Fig. B1.2
The six rosettes for n = 5

Using a 'rhomb-shuffling' computer program, I once found forty-nine different rosettes for n = 6, but my program may have missed some.

If we perform a variation on Miss Wild's tangent-circles construction for the half-integer n-values 3 ⁄ 2, 5 ⁄ 2, and 7 ⁄ 2, we obtain the pseudo-compound rosettes shown below. The 2n quadrangles incident at the center of the large circle are kite-shaped; all the other quadrangles are rhombs.
In a pseudo-compound rosette of order n, there are n − 1 ⁄ 2 different shapes of quadrangle, and there are 2n specimens of each shape.
In every kite, the face angle at the vertex opposite the central vertex is equal to π ⁄ 2n.
If each kite were elongated by translating its central vertex to the nearest vertex on the kite's symmetry axis, it would be transformed into a rhomb.


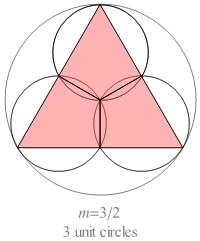
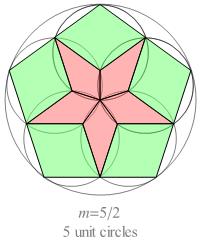
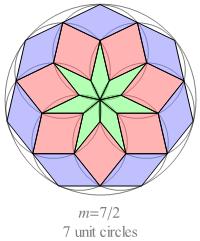
Fig. B1.3
Pseudo-compound rosettes for n = 3/2, 5/2, and 7/2
(cf. Fig. C3.9.3)

Let's call the arrangement of polygons inside each small circle in a pseudo-compound rosette a pseudo-STRAWBERRY.

Prove that neither the tiles in a pseudo-strawberry nor those in a pseudo-compound rosette can be arranged in any other pattern with convex boundary.

I don't recall ever hearing Miss Wild mention that the rhombs in a compound rosette can be rearranged to form other patterns. I first learned about rosettes as mathematical objects from Coxeter's description of them as projections of polar zonohedra, in his Regular Polytopes, Third Edition, Dover Publications (1973) pp. 27-30. Coxeter also describes them briefly in Mathematical Recreations and Essays, Thirteenth Edition, Dover Publications (1987) pp. 141-142. (In a footnote on p. 141, Coxeter asks in how many ways the regular 2n-gon can be dissected into n(n − 1) ⁄ 2 rhombs. It is easy to prove that for n = 2, 3, 4, and 5, the numbers are 1, 1, 1, and 6, respectively.)


H.S.M. ("Donald") Coxeter
1907-2003

When you design a symmetrical rosette 'by hand', after deciding on the order n and the symmetry class it's natural to wonder whether there are alternatives to simply shuffling paper rhombs in hit-or-miss fashion. In 1978, while examining dozens of examples, I succeeded in sniffing out a few simple numerical rules that significantly reduce the labor. In 1979 I wrote an unpublished summary of some of those rules, but I included only a few proofs. At that time, I was able to prove only a few of the main results.

One of these rules is useful for designing rosettes of dihedral symmetry. It generates a list of all the partitions of a diametral pendant into two radial pendants of equal projected length. A diametral pendant is a string of rhombs joined tip-to-tip, lying along a line of reflection symmetry and extending from one boundary vertex to the opposite boundary vertex. Diametral pendants are the 'structural ribs' of dihedral rosettes.

A second rule, which is is useful for designing rosettes with cyclic symmetry, generates a list of all the partitions of a ladder into two half-ladders of the same projected length. A ladder is a strip of rhombs in a rosette that extends from one edge of the {2n} to the opposite edge. Every rhomb in a rosette belongs to two intersecting ladders.

You can learn about part of what I discovered in 1979 about both cyclic and dihedral rosettes here, in a condensed version of the 1979 report. I plan to expand this note soon. I will describe complete proofs of all of the claimed results. (It wasn't until 1991 that I returned to the subject of rosettes and succeeded both in proving what until then had been only conjectures and also in expanding some of the results. I was pleasantly surprised to find that only elementary methods were required for all the proofs.)

In 1979 I mailed copies of my report on rosette design rules to several mathematicians, hoping that someone would provide the missing proofs.
Ira Gessel, who had been given a copy of the report by Gian-Carlo Rota (one of the experts on my mailing list), sent me an extremely helpful reply.


Fig. B1.4
Ira Gessel

With Ira's permission, I include his reply here. Ira's letter explains that the rhombs in each ladder of a rosette are the duals of points of intersection in an arrangement of n chords of a circle, indexed in order of their angular orientation. The sides of each rhomb are perpendicular to the two chords whose intersection is the dual of the rhomb. This means that one can generate rosettes by a simple 'automatic' method, without having to shuffle paper rhombs. After receiving Ira's letter, I wrote a Fortran program to implement his algorithm, and my first-semester computer graphics students were soon creating examples by the dozen of rosettes of various orders n. Rosettes generated by this method typically differ in appearance from the ones my students had been creating 'from the ground up' by applying the diametral pendant and ladder partitioning rules I had taught them. The 'automatic' rosettes tend to be somewhat bland in appearance. Later, after I have defined the total curvature of a rosette, the reason for this difference will become clear. (The strawberry appears to have the smallest possible value of total curvature. I conjecture that this is true for every n.)

At the January meeting of the AMS in San Antonio a few months after I had mailed out copies of my rules report, I showed a copy of it to Ron Graham.


Ron Graham

Paul Erdös, Ron's friend and collaborator, was standing a few feet away. After briefly examining the report, Ron introduced me to Paul and asked him if he would mind looking it over. Paul scrutinized it for a few minutes and then said,

     "Zeese is veddy in-ter-est-ing. Zee next time I am in Car-bon-dale, vee vill prove zeeze sings too-ged-der."


Paul Erdös
1919-1996

Although I was intrigued by the possibility of someday having an Erdös number of one, that will never happen, because there was no 'next time'. Later that year, Mel Nathanson, Paul's regular host in Carbondale, left SIU for Rutgers, and Paul never returned to Carbondale.


Mel Nathanson


In 2007, the algebraist Bob Fitzgerald compared the 'vanishing sum of sines' equations predicted for n = 15 and n = 18 by the ladder partitioning rule (described here) with a set of equations, known to be complete, that he obtained by invoking cyclotomic field theory. Here's the email Bob sent me. He had confirmed that for n = 15 and n = 18, every possible equation of this vanishing-sum-of-sines type is at most a linear combination of the equations derived from my rules for ladder partitioning.

Below are scanned images of examples of rosettes, almost all of which were drawn (long ago) with TrueBASIC.



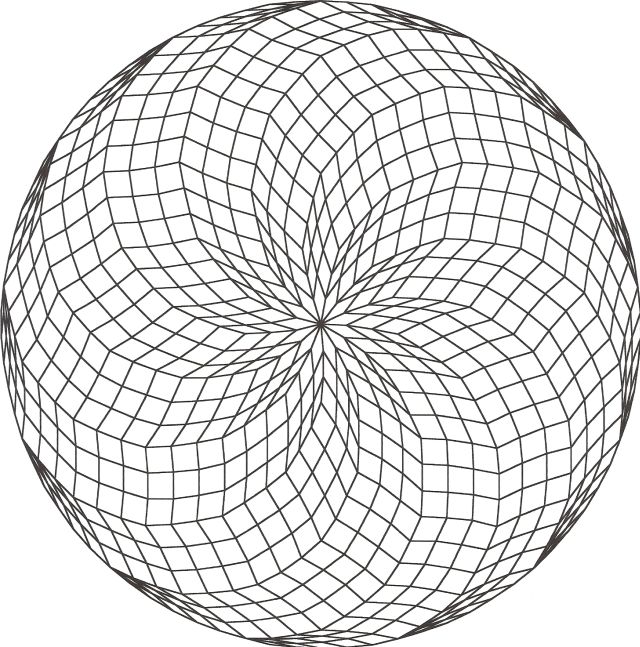
Fig. B1.5
n = 39
c13
pdf version


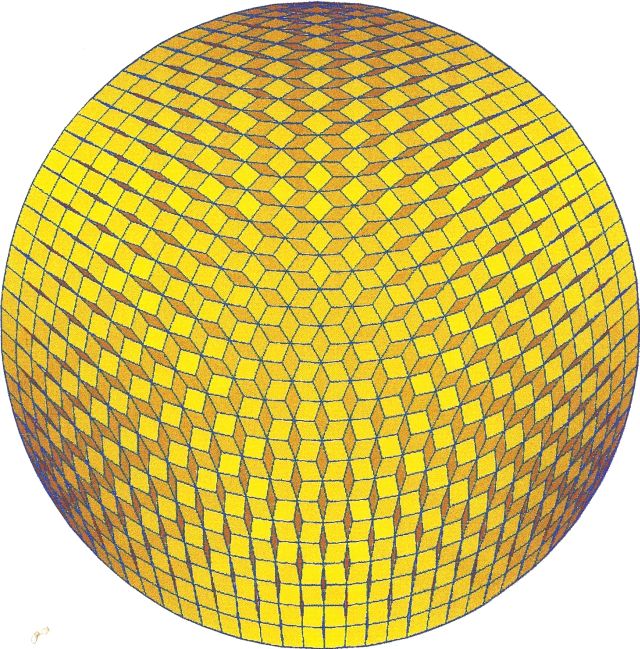
Fig. B1.6
n = 36
d3
pdf version

The image in Fig. B1.4\5 is the result of a search for rosettes that contain the maximum possible number of convex hexagons (call them ovals) tiled by three rhombs. In 1980 I examined hundreds of rosettes without finding any examples containing fewer than n − 2 ovals. I widely circulated—but didn't publish—the conjecture that in every rosette of order n, there are at least n − 2 ovals. (I did describe this conjecture in my 1994 ROMBIX manual supplement, where − on p. 33 − it is called 'Conjecture 4.13.1'.)

When I mentioned the n − 2 ovals conjecture to Jim Propp in 1995, he immediately circulated it, with my permission, by email. (I hadn't yet opened an email account.)


Fig. B1.7
Jim Propp

Almost immediately, in an email to Jim, Alex Postnikov cited a proof by A. Yu. Belov of a statement that is more general than the statement of the conjecture, because it is not restricted to two dimensions:

In any non-trivial arrangement of n hyperplanes in k-dimensional space there are at least n − k bounded simplices.


Fig. B1.8
Alexander Postnikov

(A simplex is bounded, in Postnikov's words, if its interior is not intersected by any hyperplane.) Belov's paper, On a problem of combinatorial geometry, was published in Russian Math Surveys, Vol. 47 (1992), pp. 167-168. Alex said that he and Igor Pak had developed another proof 'in a more general context, based on the fact that every (n − k)-dimensional polyhedron has at least n − k edges going out of every vertex'.

In two dimensions, the simplices are the triangular interstices defined by the pairwise intersections of lines. The lines are not required to be straight, but any pair of lines is required to have only one intersection. If they are not straight, they are called pseudo-lines. I suspect that it may be unknown whether there exists a dual configuration of straight lines for every possible rosette.


February 29, 2009
Well, that 'suspicion' of mine was dead wrong! When I wrote to Alex and asked him about it a few hours ago, he replied that it is false, and he even described how to construct counterexamples. He wrote, "There are rhombus tilings that cannot be represented by straight lines. Equivalently, there are pseudo-line configurations that cannot be straightened. ... Moreover, for sufficiently large n almost all pseudo-line configurations cannot be straightened."

(I think I'll take a short break before doing any more wild conjecturing.)


Now back to the rosette gallery:


Fig. B1.9
n = 45
c9
pdf version


Fig. B1.10
n = 45
c15
pdf version


Fig. B1.11
n = 45
c15
(The colors are reversed with respect to the arrangement in Fig. B1.6.)
pdf version


Fig. B1.12
n = 39
c13
pdf version


Fig. B1.13a
n = 27
c9
pdf version


Fig. B1.13b
n = 27
c3


Fig. B1.13c
n = 27
d3


Fig. B1.14
n = 49
c7
pdf version


Fig. B1.15
n = 50
c5
pdf version


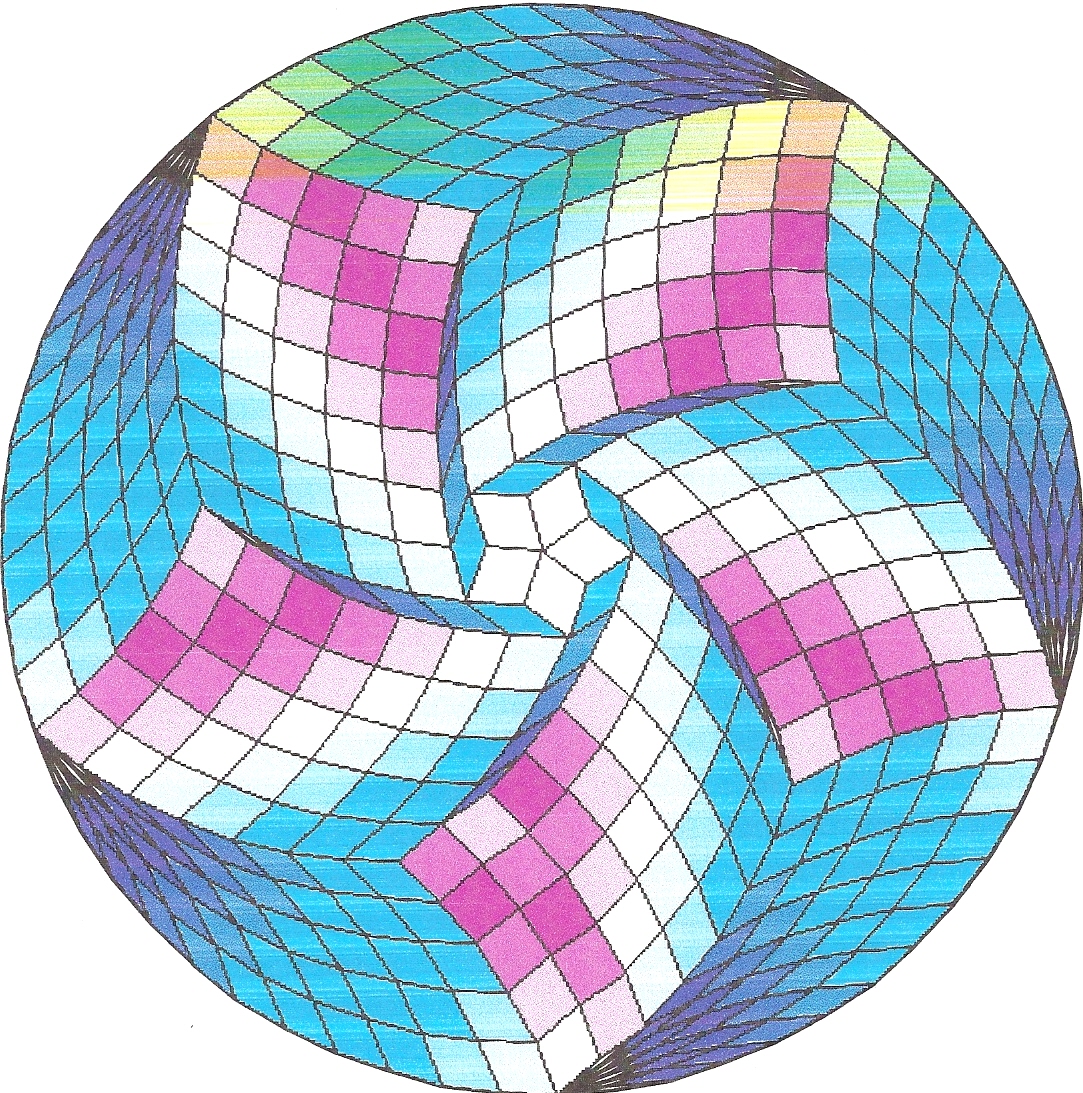
Fig. B1.16
n = 50
c5
pdf version


Fig. B1.17
n = 27
d1
(redrawn with Mathematica)
pdf version


Fig. B1.18
n = 27
d1
(redrawn with Mathematica)
pdf version


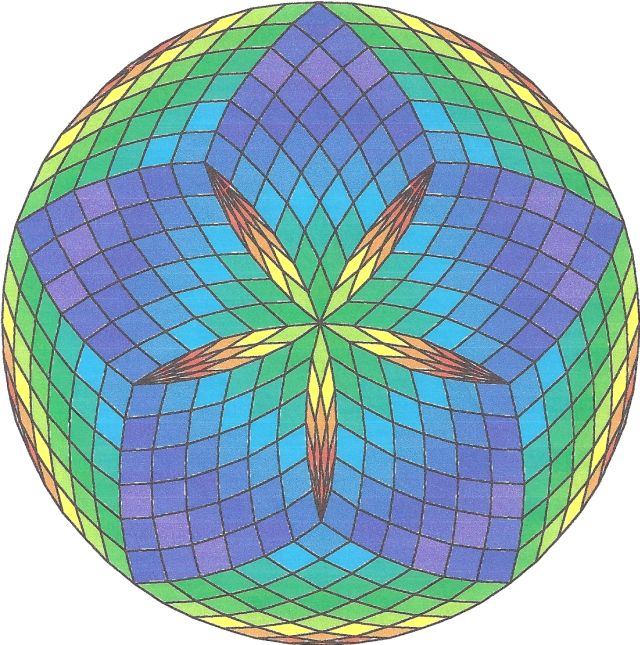
Fig. B1.19
n = 30
d5
pdf version


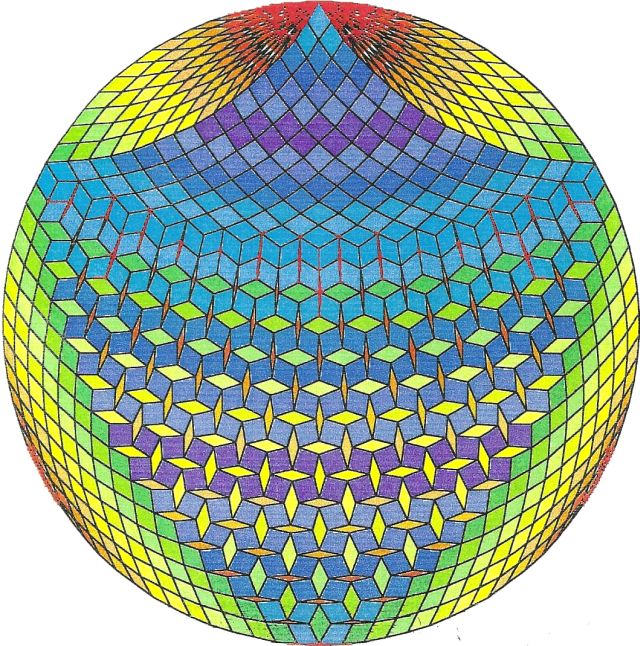
Fig. B1.20
n = 45
d1
pdf version


Fig. B1.21
n = 45
d9
pdf version


Fig. B1.22
n = 25
Rosette designed by an S.I.U. student in 1979

Note added in early August, 2013

Yesterday I spent a couple of hours searching through a bunch of old files, looking for stuff to throw out in order to make room for new stuff. (While I refuse to admit that I'm an out-and-out packrat, I can't truthfully deny that I'm pretty lazy about regularly getting rid of stuff the way orderly people seem to have a habit of doing. So I guess there's no good reason for anybody to pay much attention to my denial of being a packrat.)

Anyway, among the barely remembered things I decided not to throw out yesterday are some of the rosette images below. I printed them in 2001, when I was using an Apple Power Mac. (Like many other people, I found the color menu to be elegantly designed.)

You'll notice that some of these images belong to a single family. They were all produced by a TrueBasic program I wrote in 2000 called ROTOTILER, which challenges the user to transform a rosette for a selected value of n, displayed in the left panel, into a rosette (for the same value of n) that is displayed in the right panel, in the shortest possible sequence of 'Ovalturns'. An 'Oval' is defined as a convex hexagon tiled by three rhombs, and an 'Ovalturn' is defined as a halfturn of an Oval. Once the user has selected the source and target rosettes from a menu, the number of Ovalturns in the minimal sequence is immediately posted at the top of the screen.

When I find time, I'll have more to say about ROTOTILER. For anybody with lots of time on his/her hands, it would be a nice project to rewrite it as an app suitable for a touchscreen device. If anybody is interested, I can send them the source code listing. My TrueBasic version required that an Ovalturn be implemented by moving the cursor to the interior of the targeted Oval and then clicking on it with the mouse. I checked out the price of touchscreen monitors in those days, but they were too pricey.


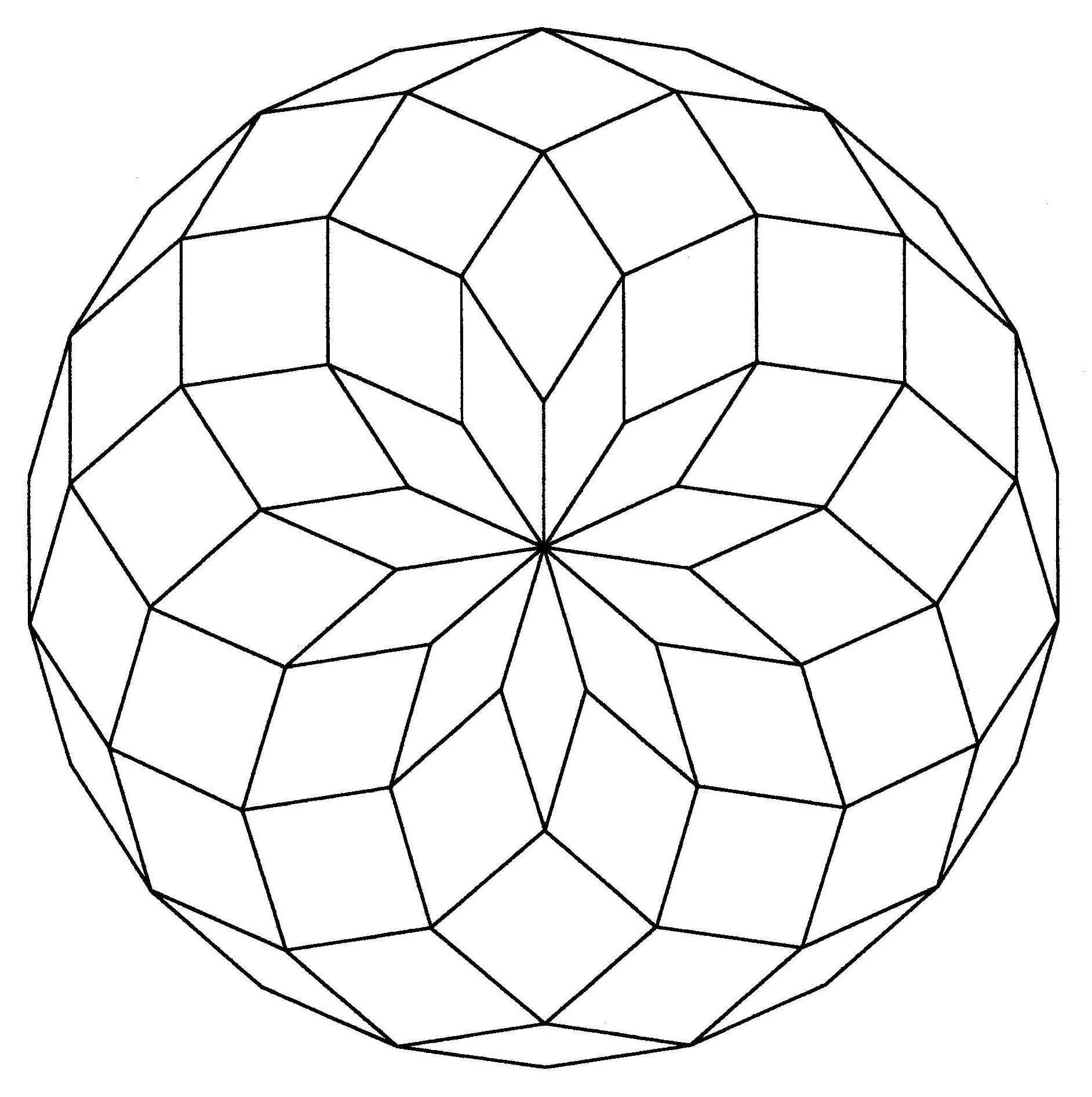
Fig. B1.23
n = 11
d11


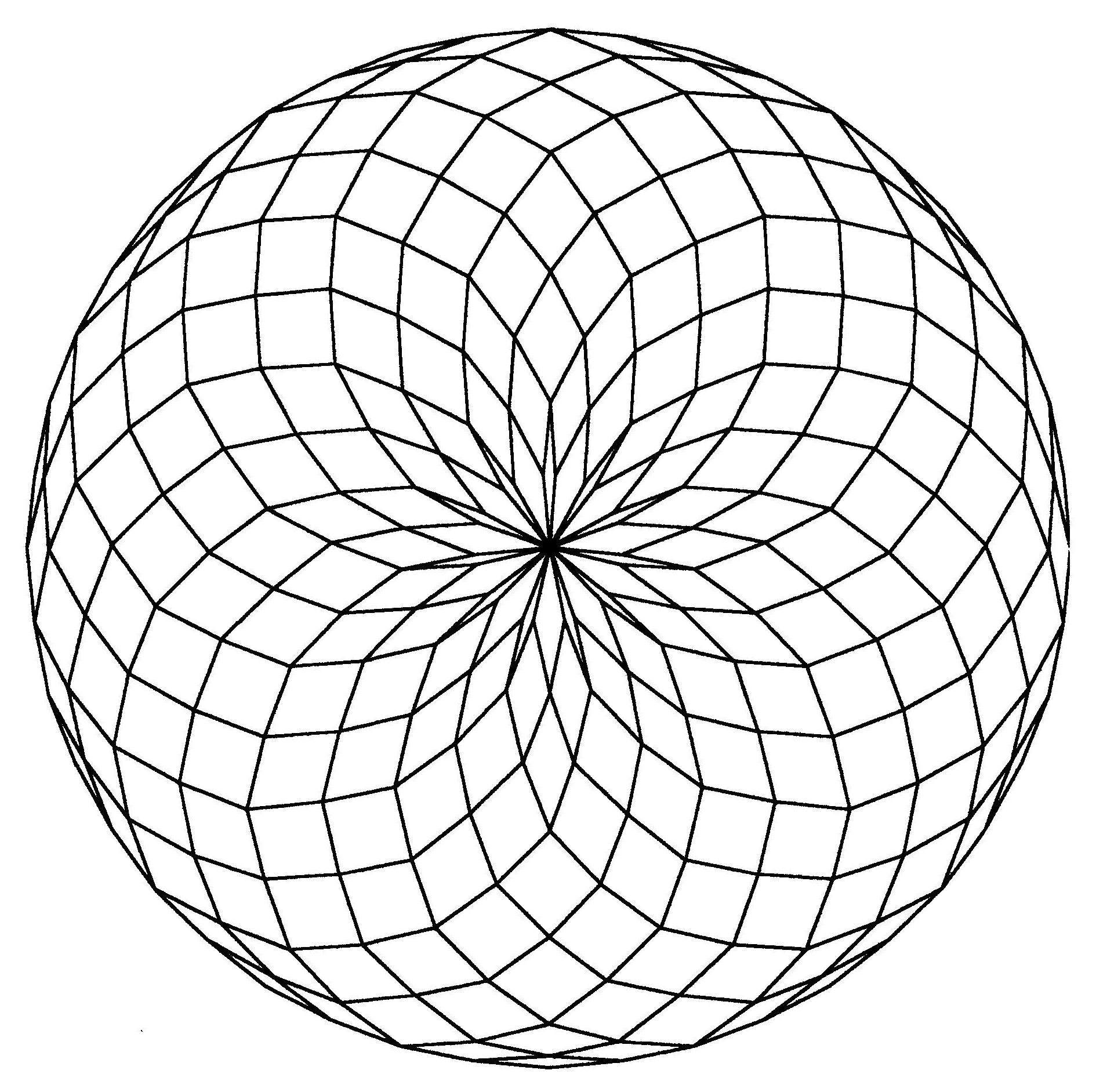
Fig. B1.24
n = 22
d11


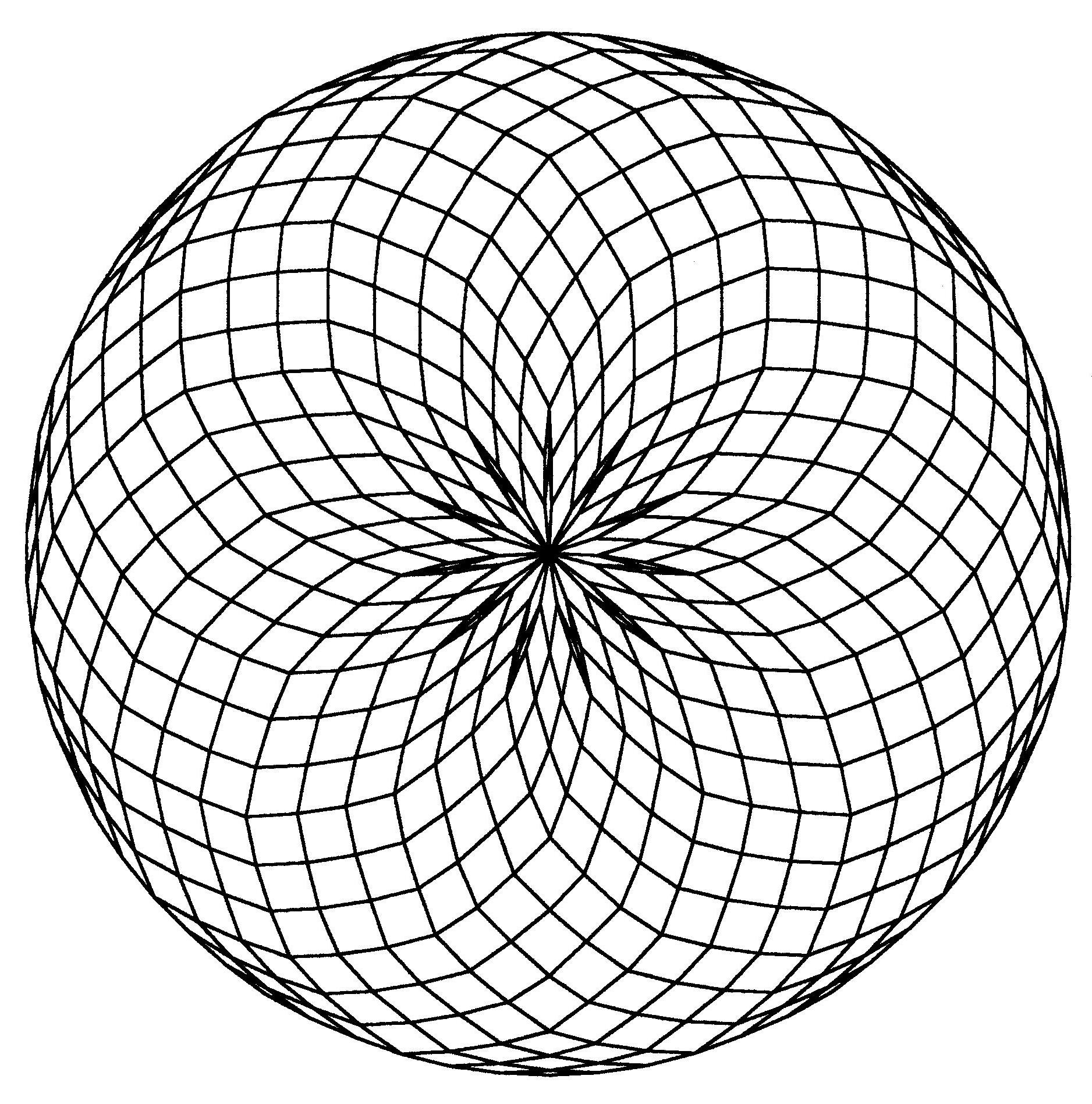
Fig. B1.25
n = 33
d11


Fig. B1.26
n = 44
d11


Fig. B1.27
n = 55
d11


Fig. B1.28
n = 66
d11


Fig. B1.29
n = 77
d11


Fig. B1.30
n = 88
d11


Fig. B1.31
n = 99
d11


Fig. B1.32
n = 99
d9


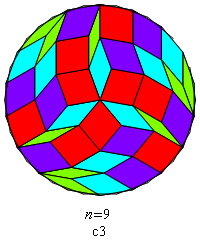
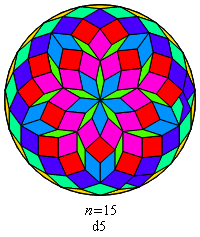
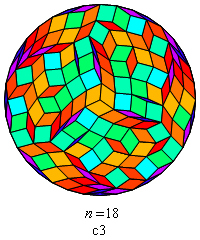
Fig. B1.24
Rosette images redrawn with Mathematica

You'll have noticed that the symmetry of all of these rosettes — whether cyclic or dihedral — is of odd order. That's no accident. It's not hard to prove that symmetries of even order are forbidden. One can prove further that the order of the allowed cyclic or dihedral symmetries is restricted to odd divisors of n (including n itself). Because a rosette that appears to have no symmetry is in fact invariant under rotation by a full turn, it is classified as having c1 symmetry (cyclic symmetry of order one).


You can make physical rosettes from magnetized plastic rhombs of SRI7, marketed under the name 'FRACTILES'.

To learn about Kate Jones' KADON's sets of translucent lucite rhombs from SRI7, look here.


B2. ROMBIX (a dissection puzzle)



'Circle tiling' by the 42 rombiks of ROMBIX-26


(Look at KADON's ROMBIX sets.)

Beginning in 1991, when ROMBIX first appeared in the marketplace, I wrote several different versions of a manual for it.



Back to GEOMETRY GARRET