K-PATTERNS
Back to GEOMETRY GARRET
Alan H. Schoen

D. K-PATTERNS: IMAGES DERIVED FROM PARTIAL SUMS OF POWER RESIDUES
(STILL UNDER CONSTRUCTION!)

   BACKGROUND

We define a K-pattern as a chain of ν unit vectors u_k, each of which joins r_k
and r_k₊₁ (k = 0,1,2,...), a consecutive pair of points in the plane, where
.
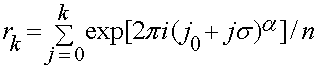The five parameters of a K-pattern — n, α, σ, ν, j₀ — are defined as follows:

   n, α, σ, ν are positive integers;
   j₀ = non-negative integer.
           n is called the modulus,
α the exponent,
σ the [loop] step,
ν the period, and
   j₀ the initial j-value.
(I am grateful to the mathematician Andrew Odlyszko, who explained to me
in 1982 that these partial sums, which underlie the images I call K-patterns,
are just generalized versions of well known expressions called Kummer sums.)
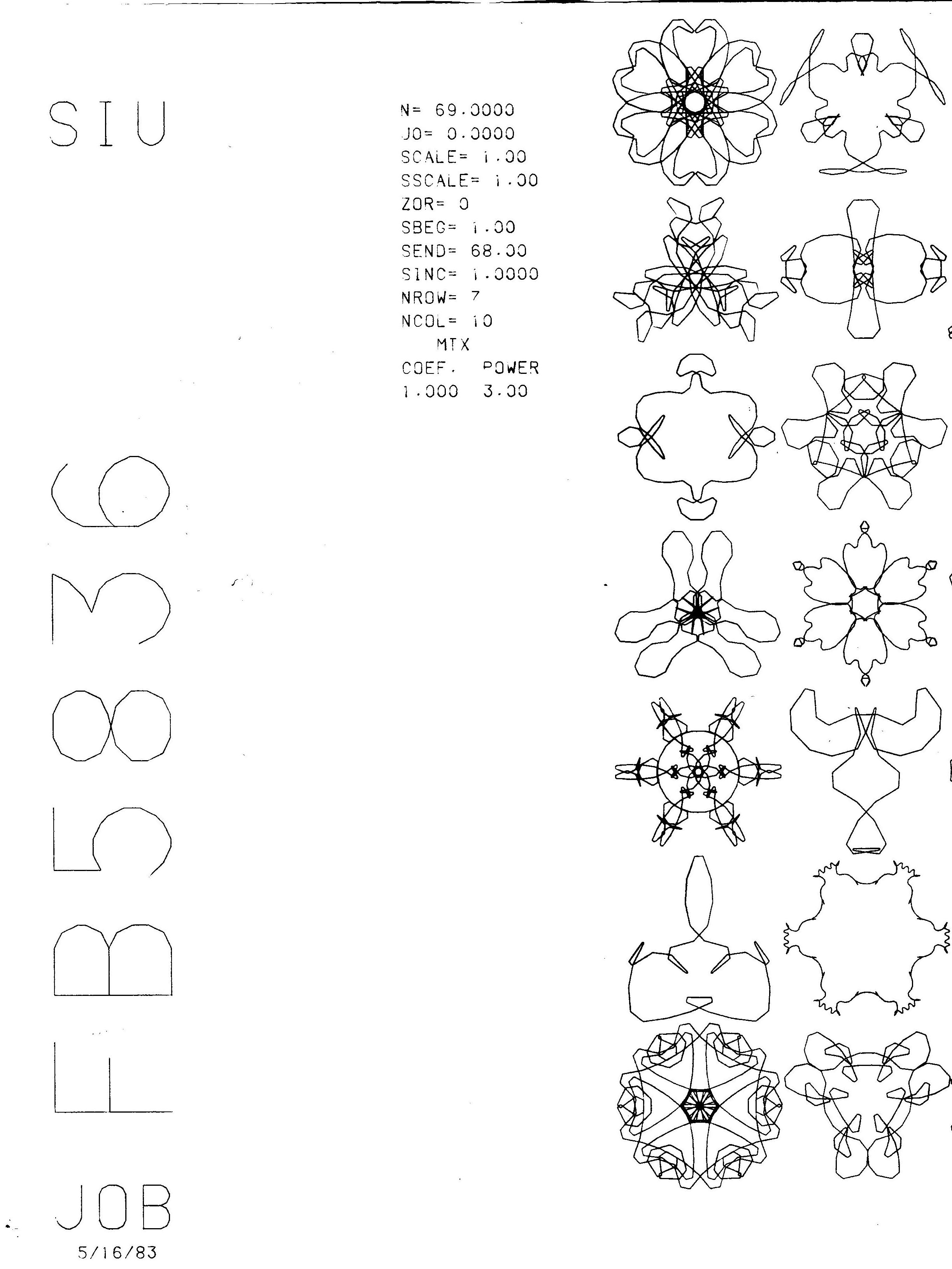
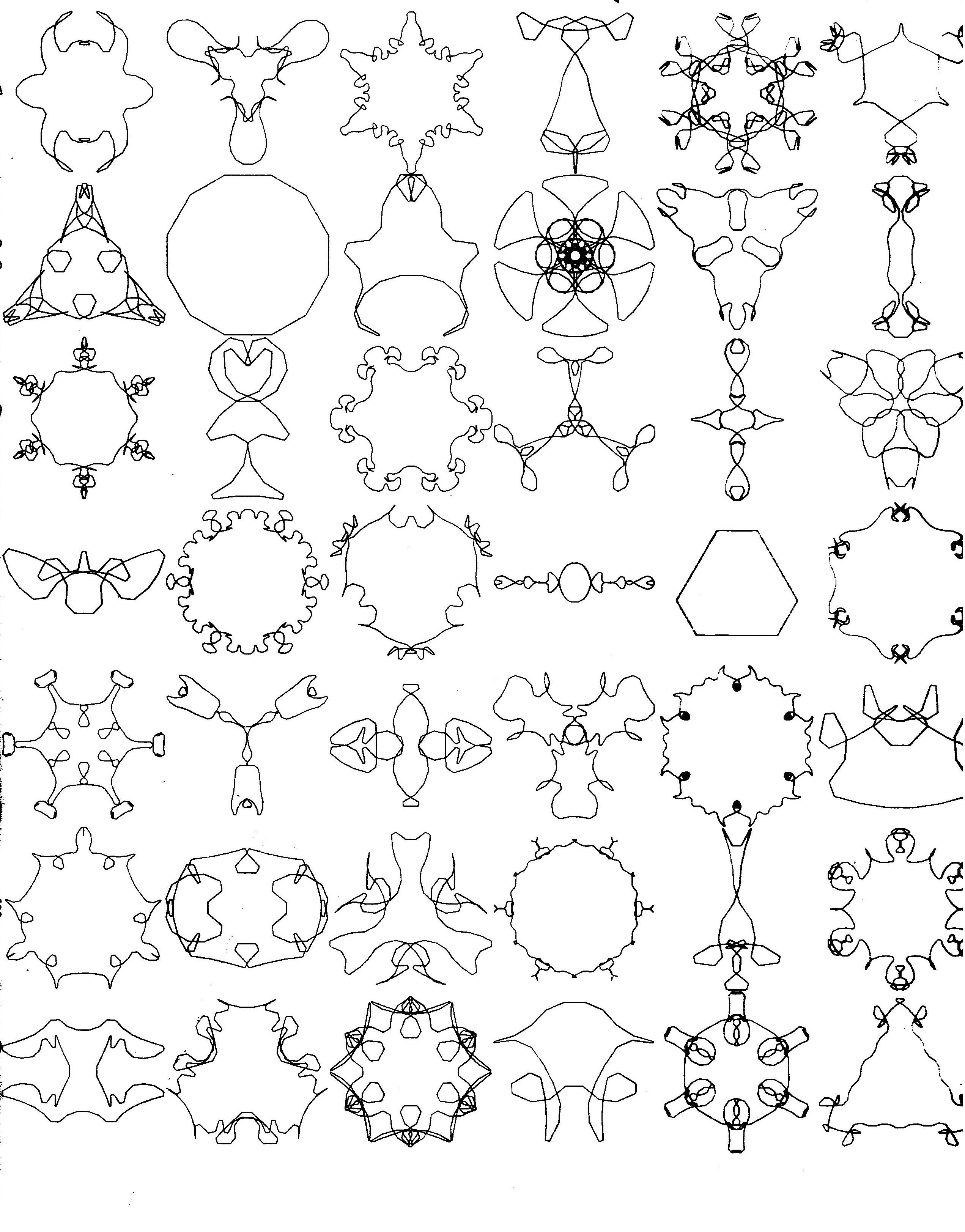
Below are the 68 different K-patterns for <n, α, j₀> = <69, 3, 0>, one for every value
of σ_i in the interval [1≤ i ≤ 68]. The images for σ₁=1 to σ₇=7 are in the left-most
   column, starting from the top. The images for σ₈=8 to σ₁₄=14 are similarly ordered in
   the second column (etc.). I'll call this arrangement 'left-to-right column order' .
(To see these Mathematica images in slightly higher resolution, click here.)
   Immediately below these images is an earlier panel showing the same K-patterns
drawn in 'rounded' style (see definition of 'rounded' below). I drew this second panel
in 1983, using a FORTRAN program and a Calcomp pen plotter.

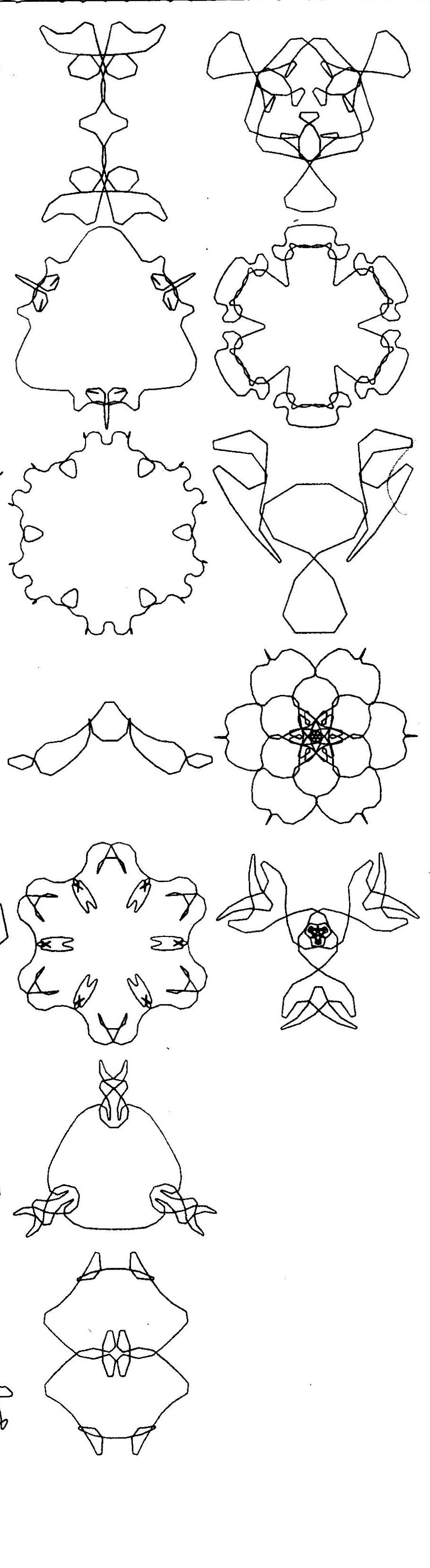
Some K-patterns are open curves, while others are closed. The open ones
(lattice curves) have translation symmetry. The symmetry and the period ν of each
pattern depend in quite complicated ways on the parameters n, α, σ, and j₀.
This survey includes a wide variety of examples of pattern families. But in order
      to develop a complete taxonomy of these patterns, one would need to investigate
the behavior of additional parameter sets and prove more comprehensive
theorems about how the period and symmetery depend on the parameters.
The emphasis here is on guessing the underlying rules by the study of examples
rather than by proving theorems. In 1983, I issued an interim report on K-patterns
    that does include proofs of a few relevant theorems, along with several conjectures.

In 1986, in Section 03 of ICM 86 at UC Berkeley (where the topic was classical number
theory), I described my Summary Report, in which I introduced an algorithm for
    assigning colors to the various line segments in K-patterns that have reflection
symmetry so that they will also display color symmetry:

"An efficient algorithm for locating lines of reflection in K-patterns —
computer graphics patterns derived from partial sums of power residues"
A few of the K-patterns shown below are rounded: instead of
   joining consecutive vertices r_k and r_k₊₁ by a unit vector u_k,
   (a) every computed unit vector u_k is divided into two collinear
half-unit vectors u1_k and u2_k (which are not plotted),
and
(b) the midpoints of consecutive half-unit vectors
..., u1_k, u2_k, u1_k+1, u2_k+1, ...
are connected by a line segment (cf. illustration below).

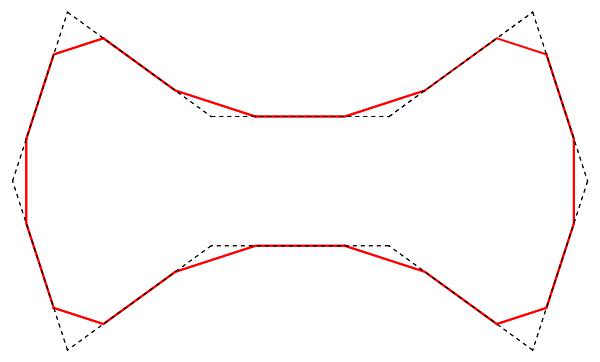
We call the dashed curve a standard K-pattern
and the red curve a rounded K-pattern.

   COLOR REFLECTION SYMMETRY

   EXAMPLES

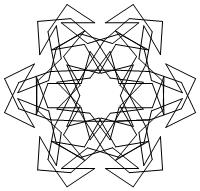
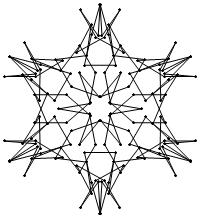
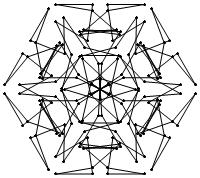
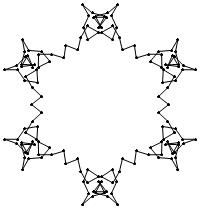
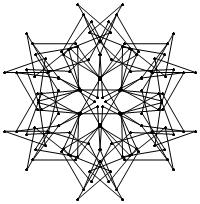
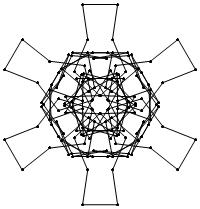
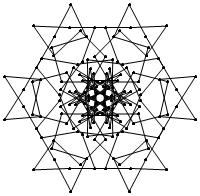
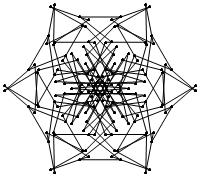
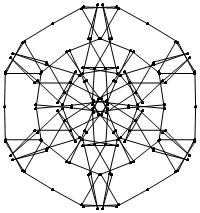
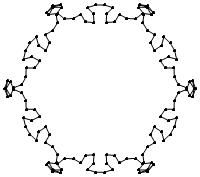
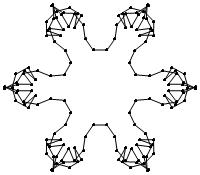
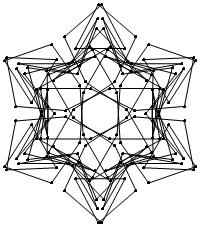
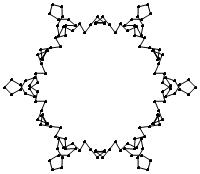
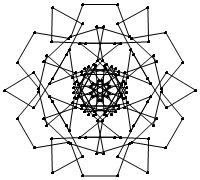
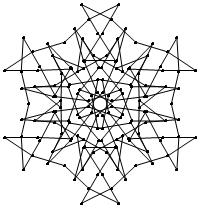
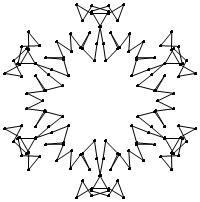
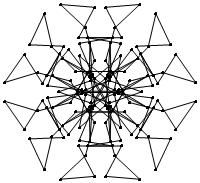
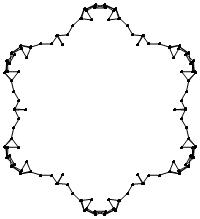
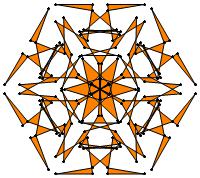
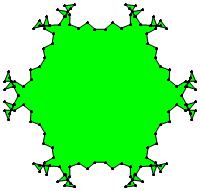
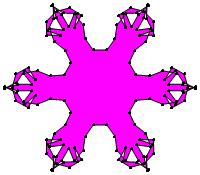
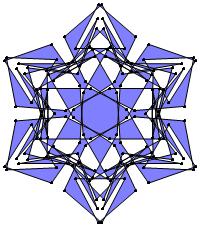
EXAMPLE: (n, α) = (3 ⋅ 5², 3)
= (75, 3)
(a)
σ = odd prime p ∋ GCD(p, n) = 1
ν = 2n
symmetry = d6
There are 20 distinct images.
The label under each image is its σ value.
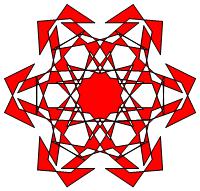
The images below were made with Mathematica.
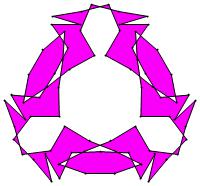
The b&w images were drawn using 'Line', while
the colored images were drawn using 'Polygon'.

      1    7       11      13       17         19       23

      29   31    37    41    43 47    49

   53 59    61    67      71 73

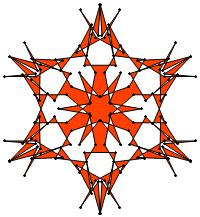
1    7       11    13       17         19    23

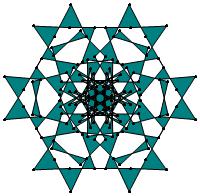
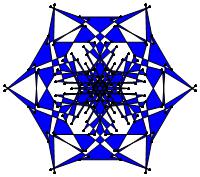
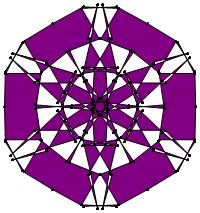
      29   31    37    41    43 47    49

53 59    61    67      71 73

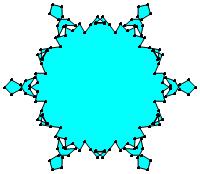
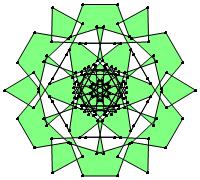
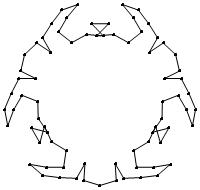
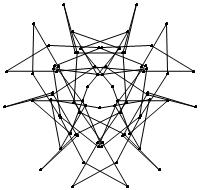
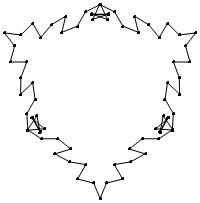
(b)
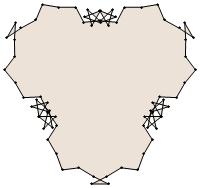
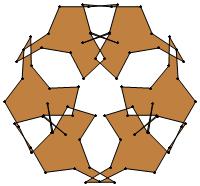
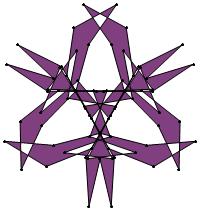
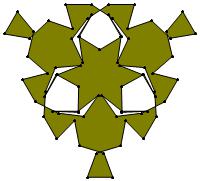
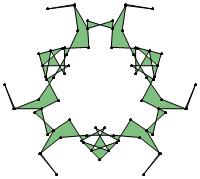
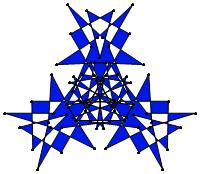
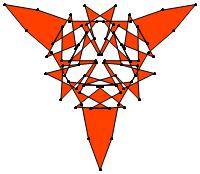
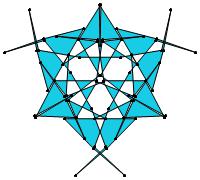
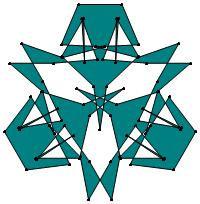
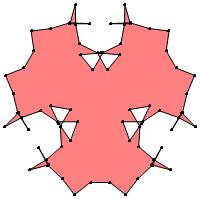
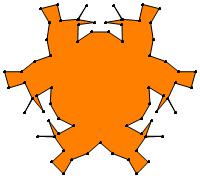
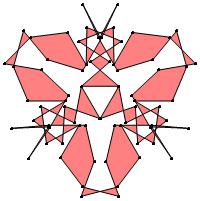
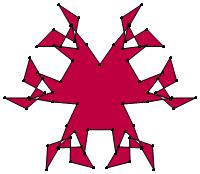
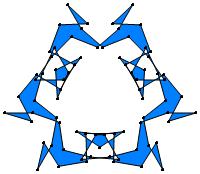
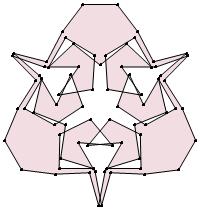
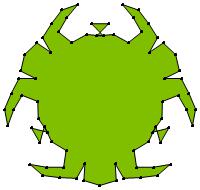
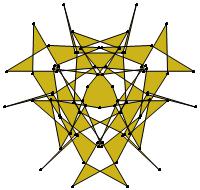
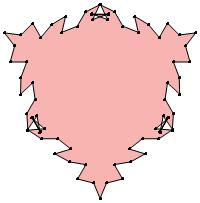
(n, α) = (75, 3)
σ = even integer i ∋ GCD(i, n) = 1
ν = n
symmetry = d3
There are 20 distinct images.
The label under each image is its σ value.

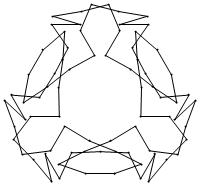
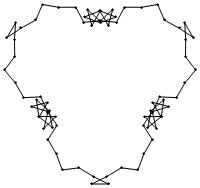
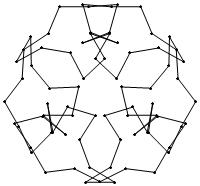
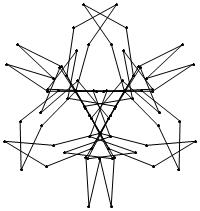
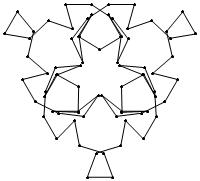
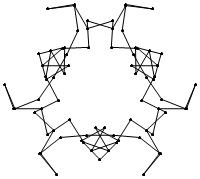
2 4   8   14      16 22

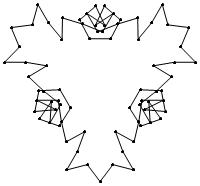
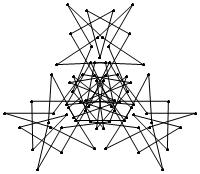
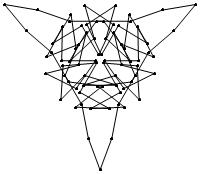
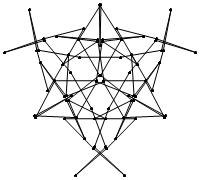
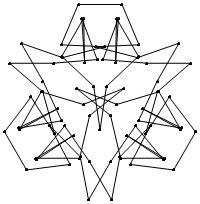
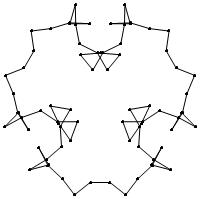
   26   28 32    34       38 44

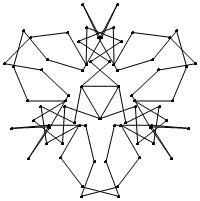
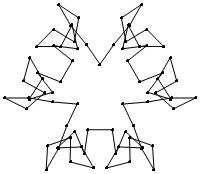
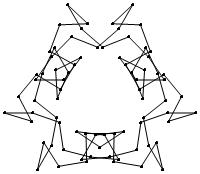
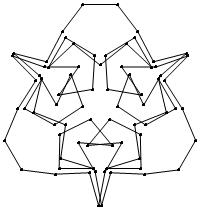
52       56 58      62      64     68    74

   2    4   8    14       16 22

   26       28    32    34      38     44    46

52       56 58      62      64     68    74

EXAMPLE: (n, α) = (5 ⋅ 3², 5)
= (45, 5)
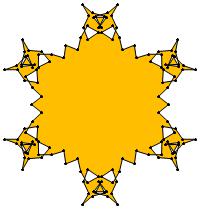
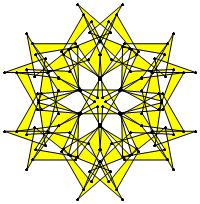
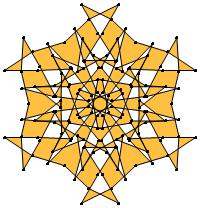
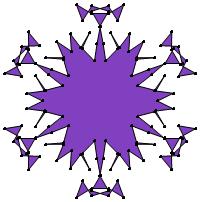
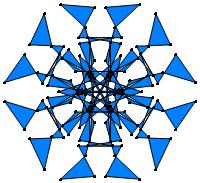
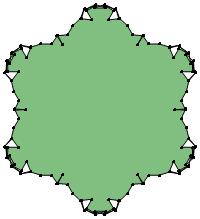
(a)
σ = either 1 or else odd prime p ∋ GCD(p, n) = 1
ν = 2n
symmetry = d10
   There are 13 distinct images, one for each allowed value of σ.

   1 3   7       11       13   17

   19       23 29    31    37 41       43

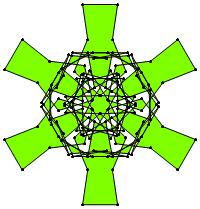
(b)
(n, α) = (45, 5)
σ = even integer i ∋ GCD(i, n) = 1
ν = n
symmetry = d5
   There are 12 distinct images, one for each allowed value of σ.

2     4   8      14    16    22

26     28     32    34      38    44

On page 9 of my 1984 interim report on K-patterns, I described a curious phenomenon I'll call pattern redumdancy: the
occurrence of a particular pattern for more than one value of the loop step σ. (NOTE: In the interim report, I used the
letter 's' instead of 'σ' to denote the loop step.) I once more gratefully acknowledge the invaluable help I received
from my former colleagues — Andy Earnest, Don Redmond, and Robert Robinson — in unraveling this conundrum.
Here is the relevant text from page 9 of the 1984 report:

Below are several examples that illustrate pattern redundancy. They
demonstrate that the requirement n ≡ 1 (mod α) is too restrictive.
EXAMPLE: (n, α) = (3 ⋅ 7², 3)
= (147, 3)
(a)
σ = every odd integer divisible by neither 3 nor 7
ν = n
symmetry = d6
There are 14 different images with d6 symmetry. Each one
is generated by three different values of the loop step
         σ in the open interval [1,2n]. We'll call these numbers
            σ₁, σ₂, and σ₃, but the same image is also generated
by three complementary values of σ, which
we'll call σ₄, σ₅, and σ₆. These complementary values are
respectively equal to 2n − σ₁, 2n − σ₂, and 2n − σ₃.
   The captions under each image list the values of
σ₁, σ₂, σ₃ (in the upper caption) and
σ₄, σ₅, and σ₆ (in the lower caption).

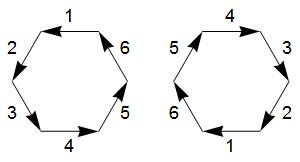
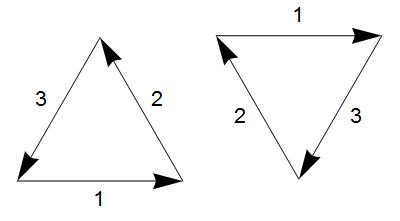
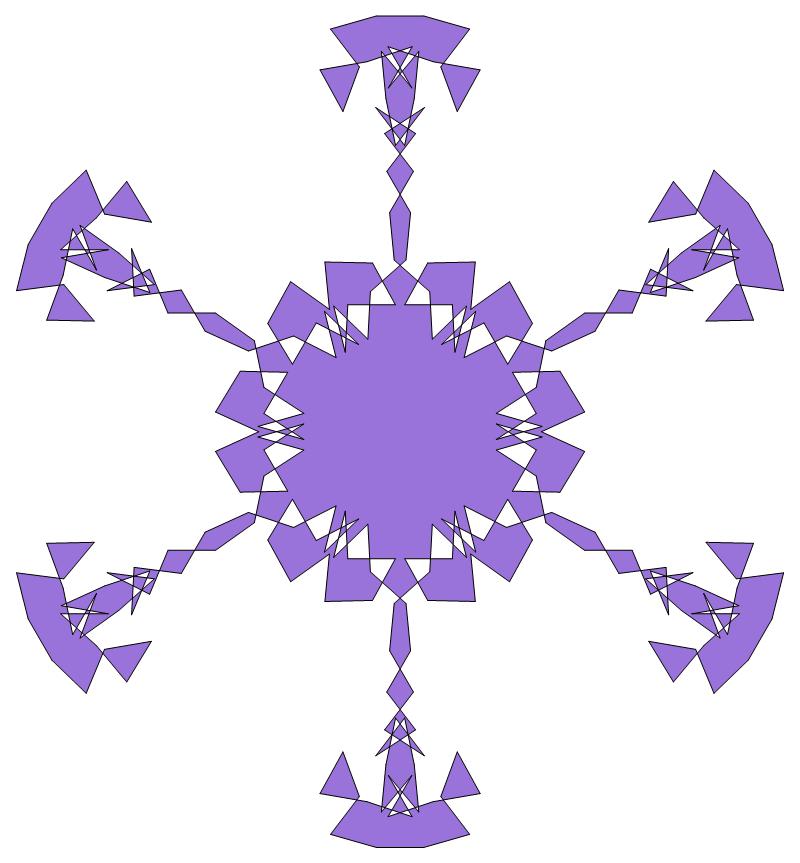
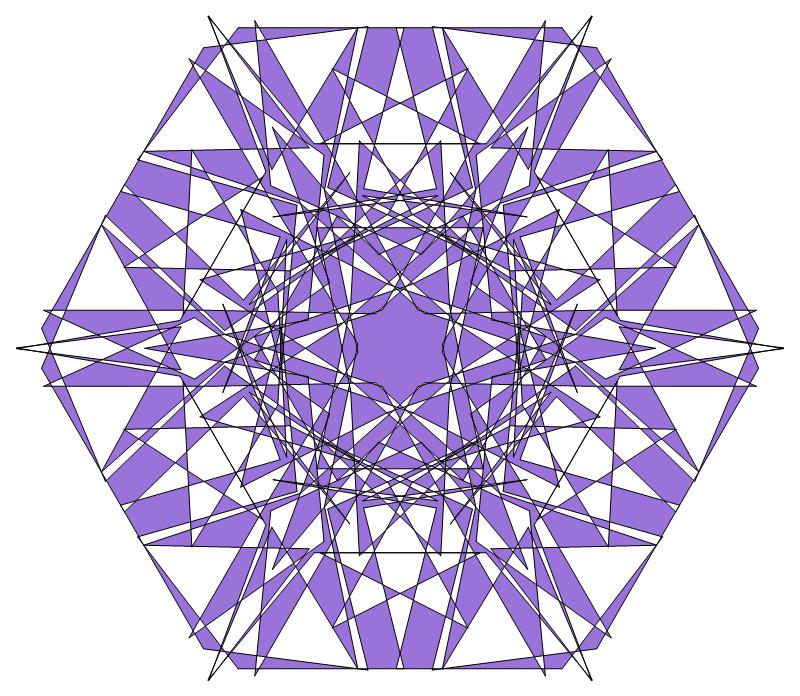
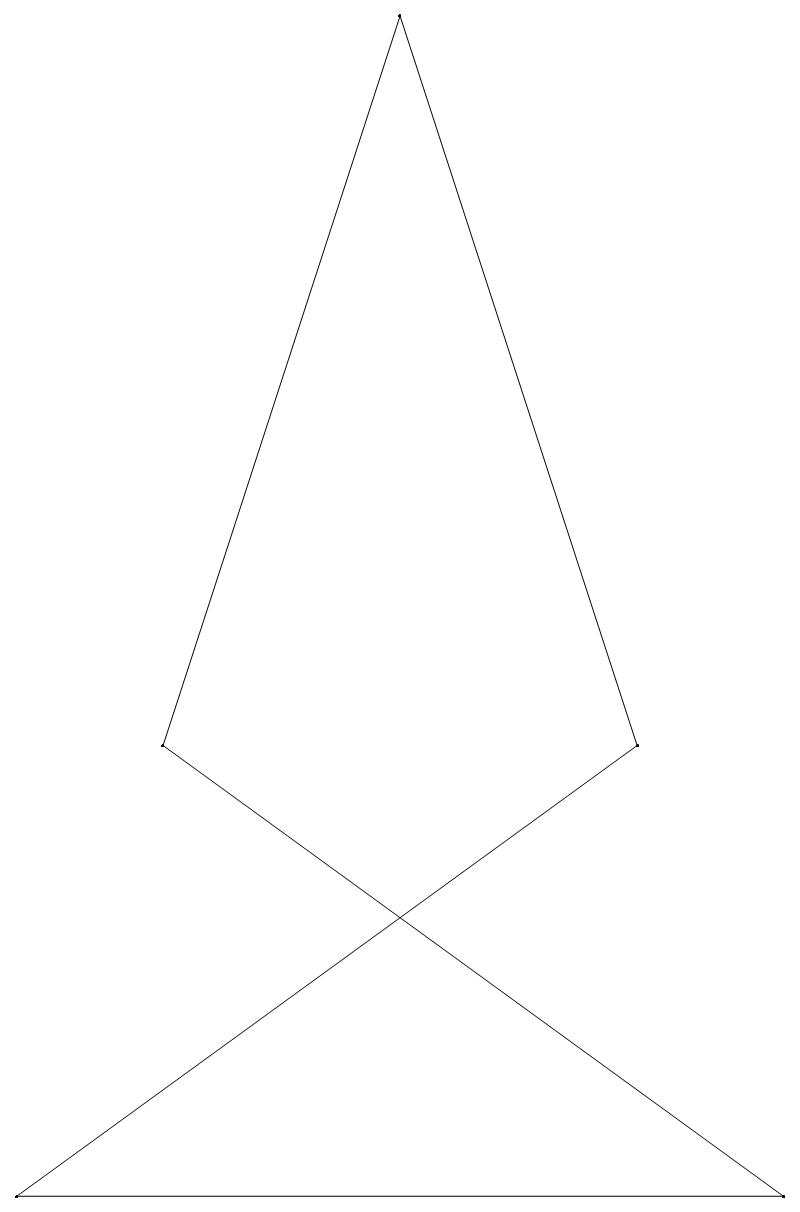
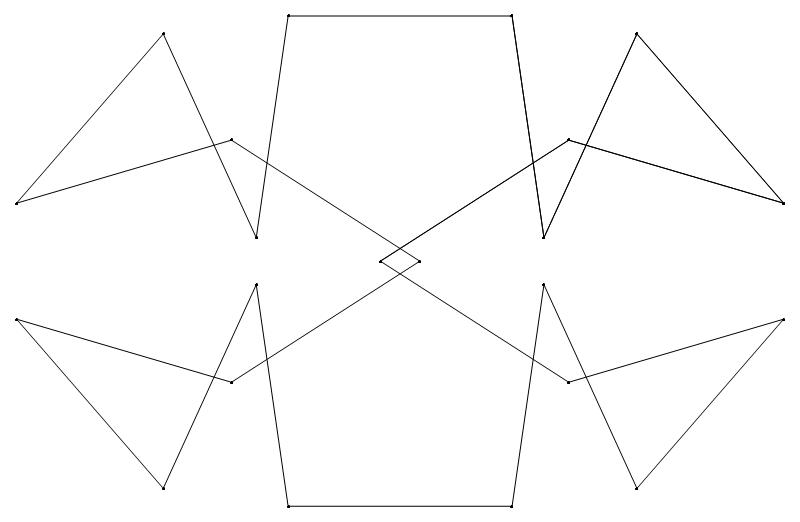
   An image with dk symmetry is symmetrical under
   inversion in its center if k is even, but not otherwise.
   Hence a d6 K-pattern, for example, will look
   exactly the same when its string of power residues —
   and therefore its constituent unit vectors —
   are arranged in reverse order. A d3 K-pattern,
by contrast, would be flipped upside-down. The two
schematic diagrams below illustrate this difference.

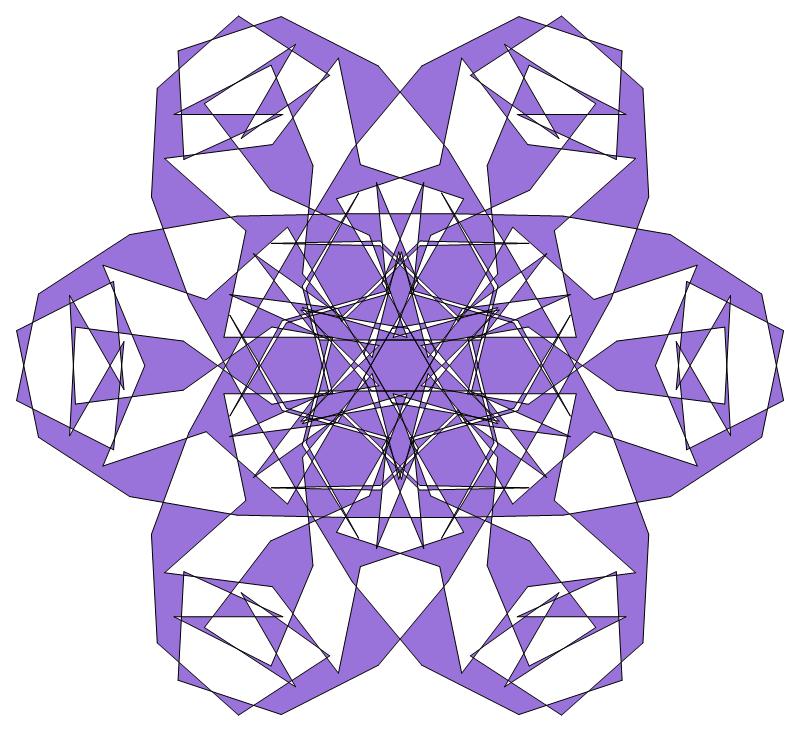
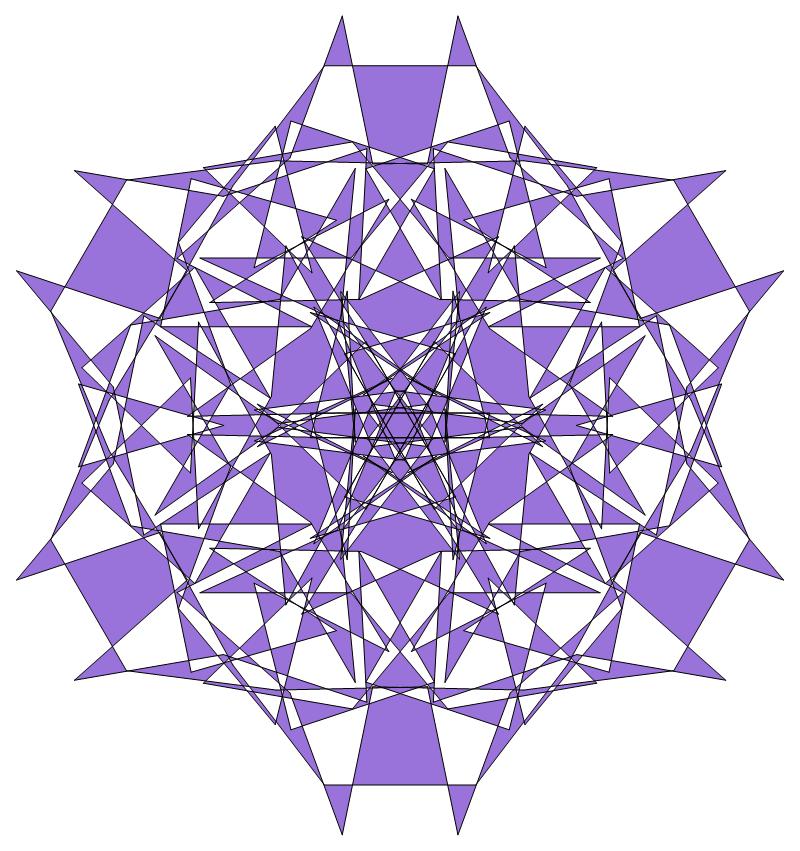
d6 pattern d3 pattern

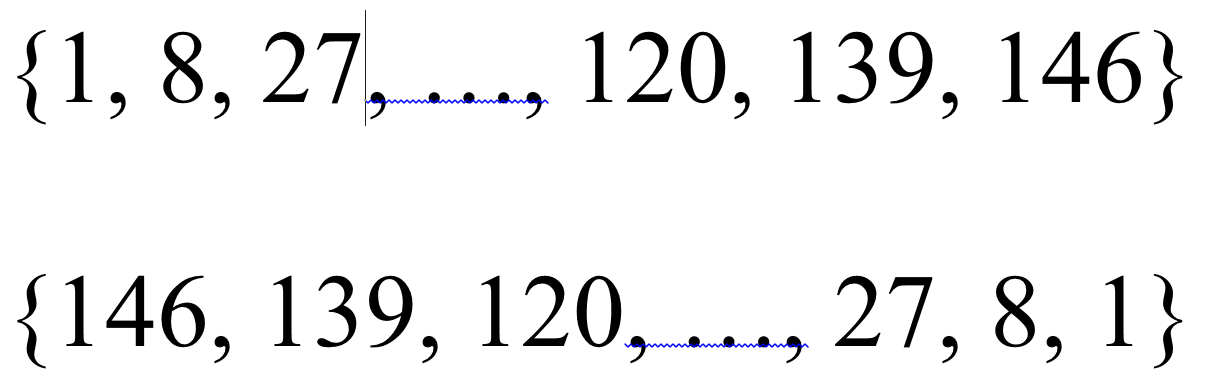
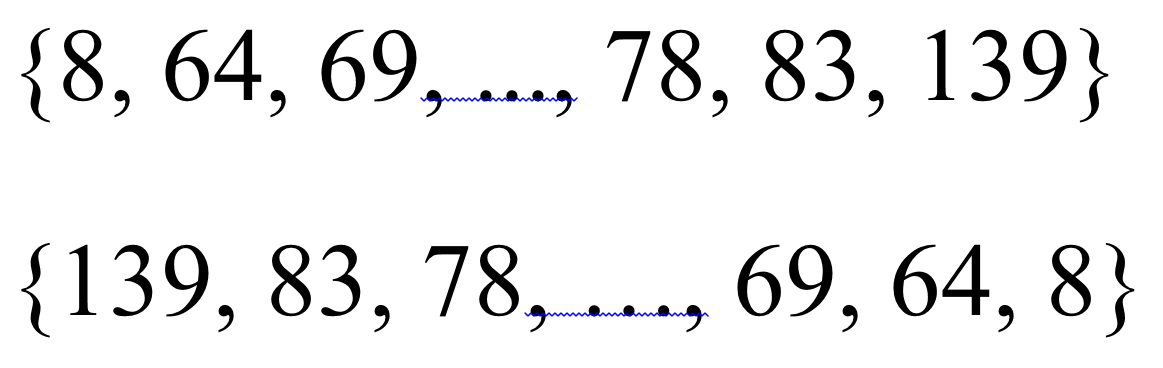
    1    67   79      5   41 101 2   11 134
   293 227 215      289 253 193 292 283 160

                 17 167 257 19   31   97    23   53   71
   277 177   37    275 263 197       261 241 223

83   89 269    61 115   29       59 131 251
   211 205 25    233 179 265        235 163 43

85 109 247     65 137 239    107 113 221
   209 185   47     229 157   55    187 181   73

95 155 191     125 143 173
   99 139 103    169 151 121

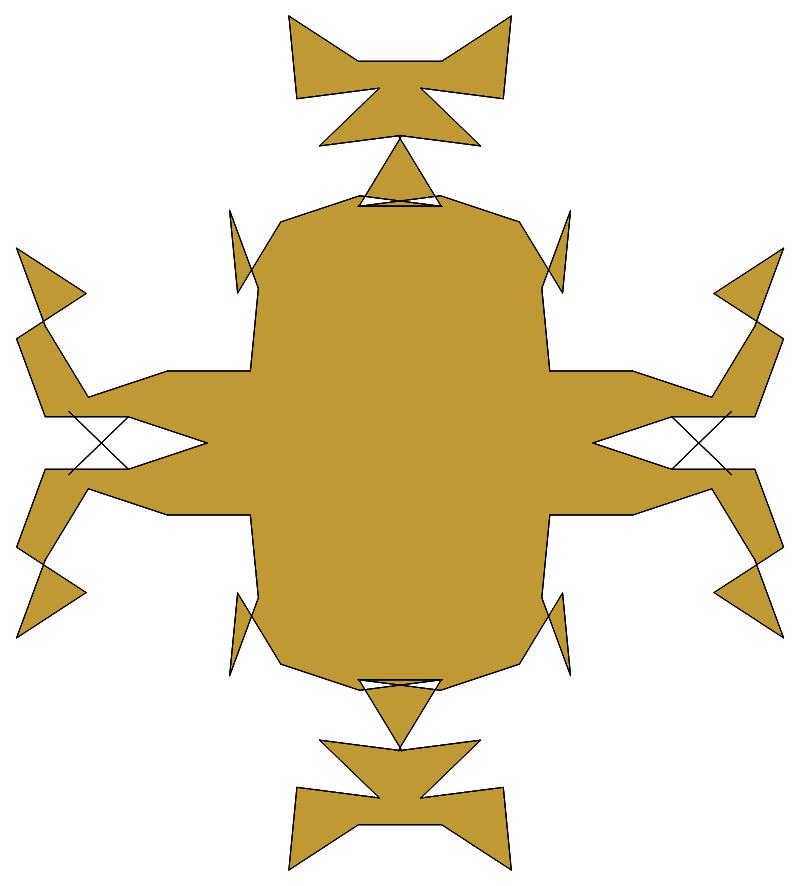
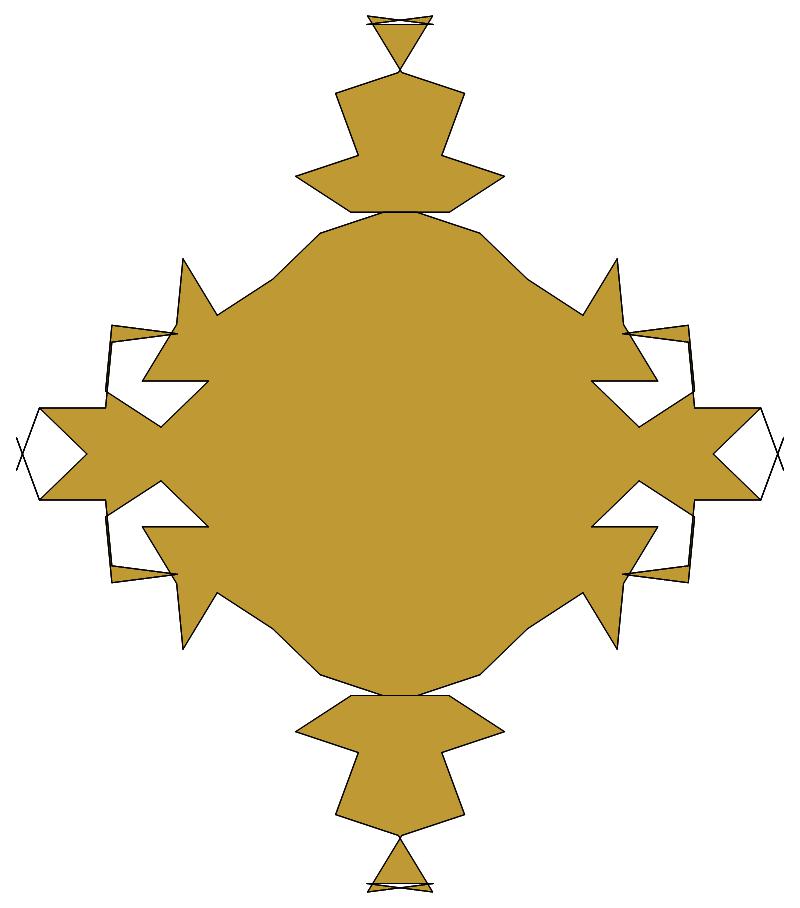
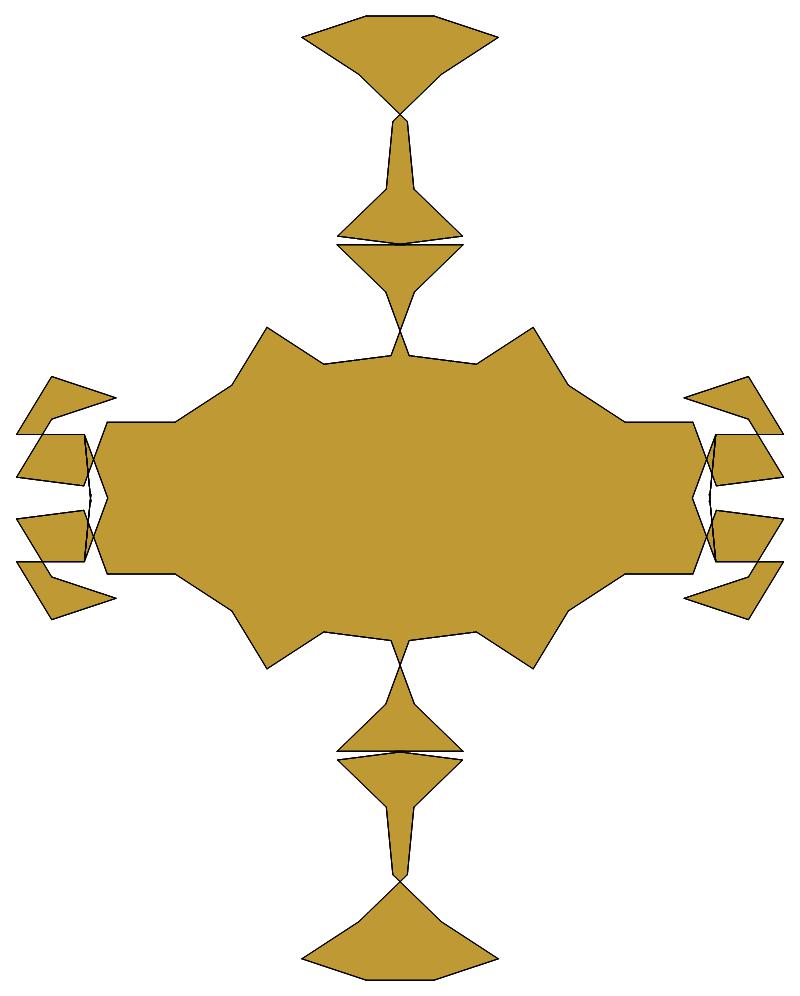
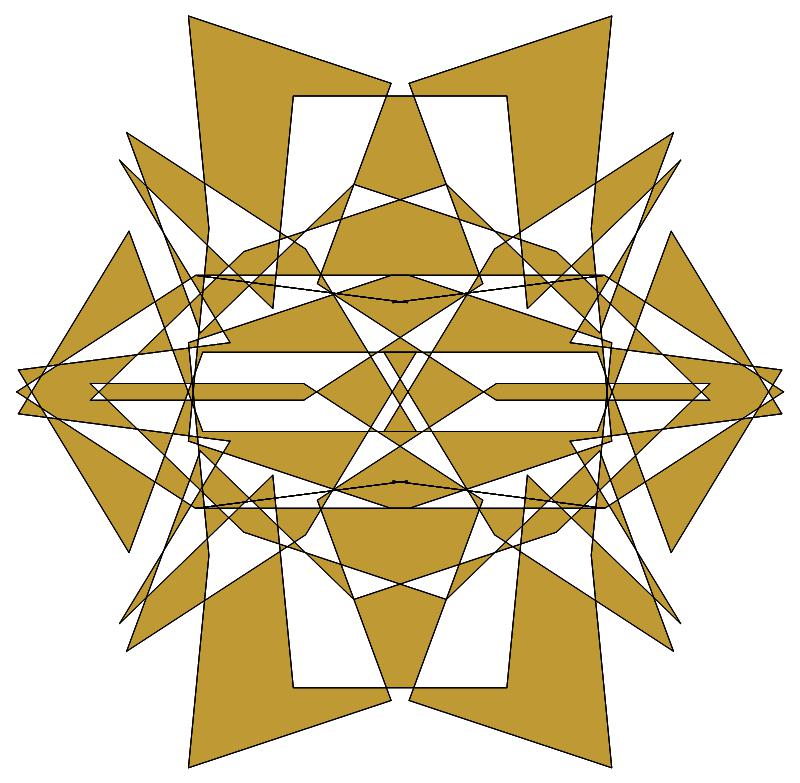
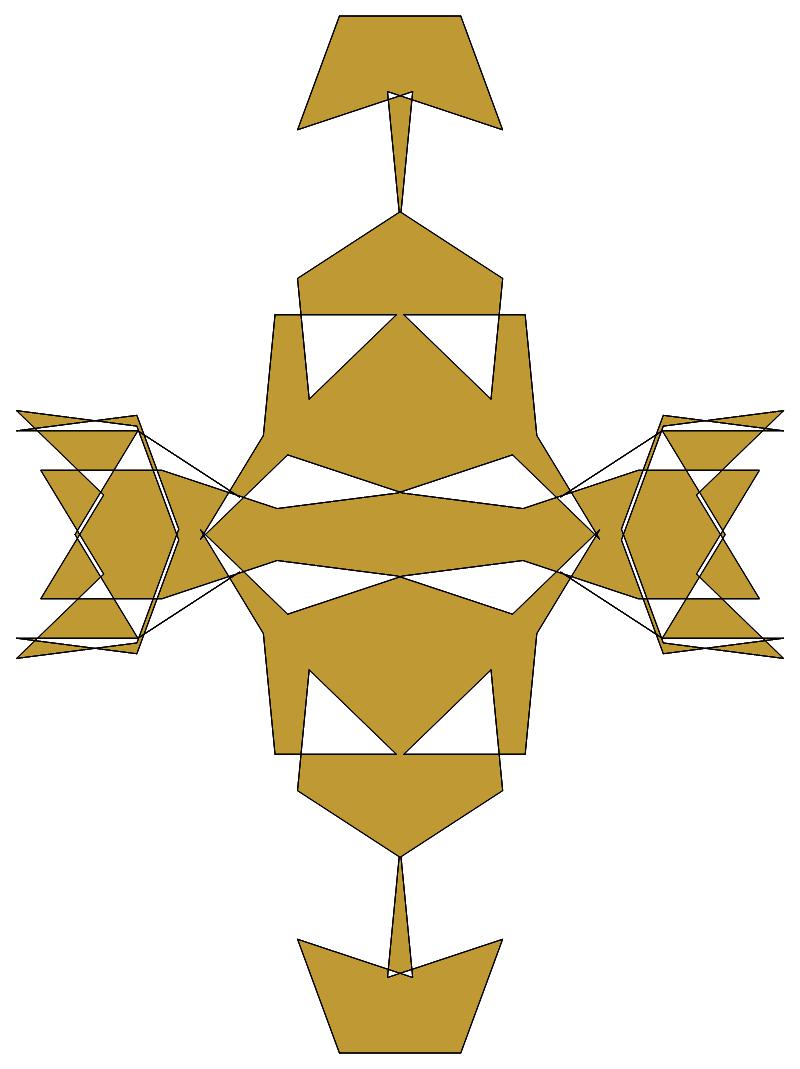
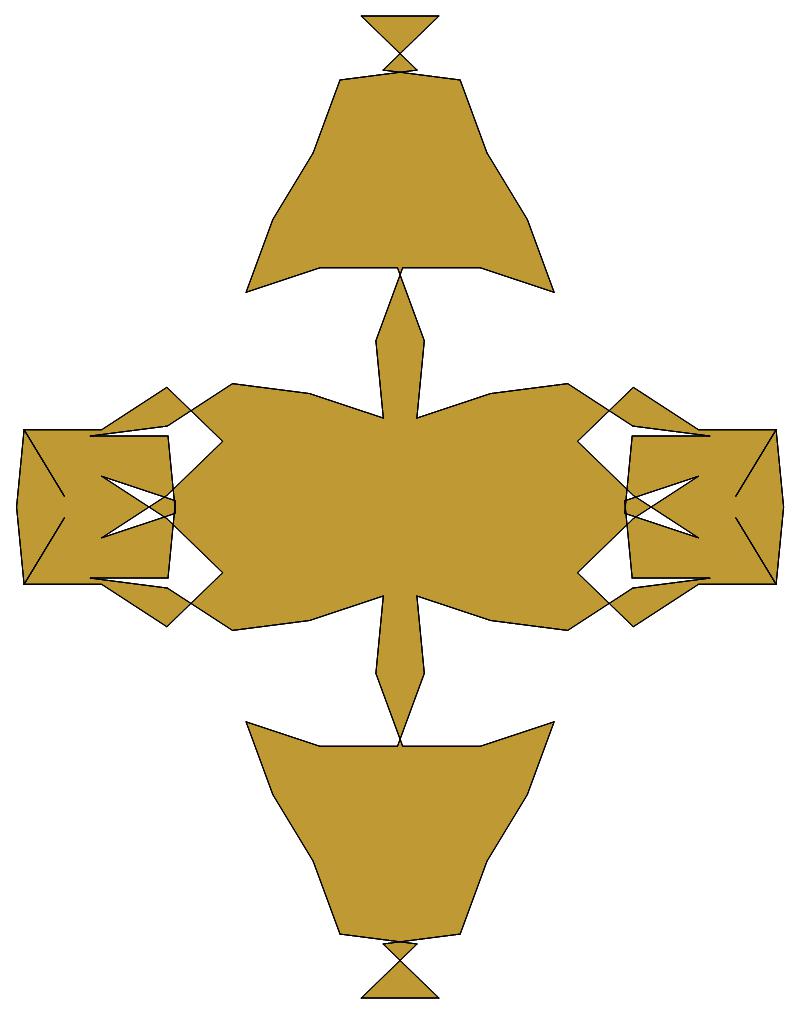
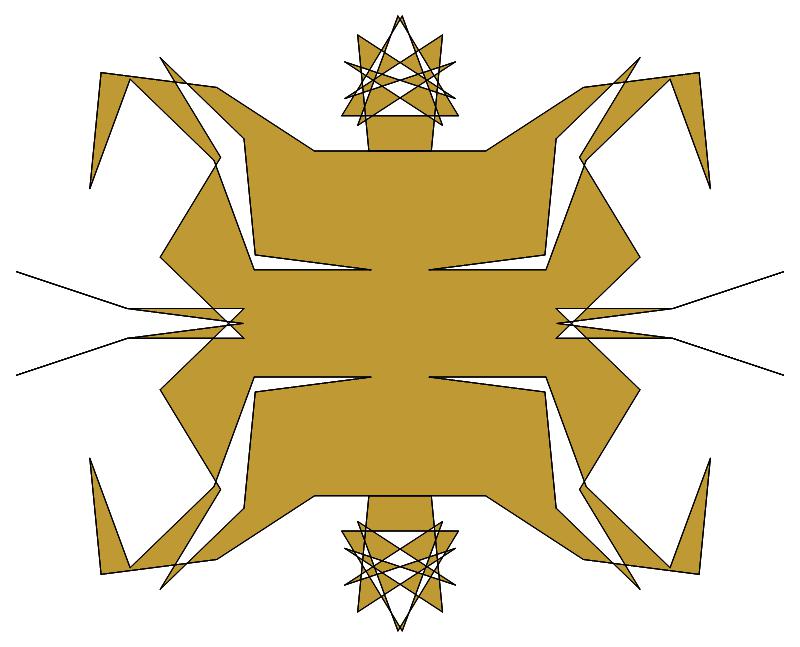
(b)
(n, α) = (147, 3)
   σ = every odd multiple of 3 that is not divisible by 7
ν = n
symmetry = d2
There are 7 distinct images, each one produced
by six different values of σ in the open interval [1,2n].
   The captions under each image list these six σ values.
   The lower captions list values of σ for which
      the order of the residues — and consequently also the
order of the unit vectors — is reversed.

   3 201 237      9    15 123    27 45 75
    291 93   57      285 279 171       267 249 219

   33 153 255     51 183 207    69 213 259
261 141 39        243 111 87    225 81 35

       99 177 165
         195 117 129

   (c)
(n, α) = (147, 3)
σ = 7 + 42k (k = 0, 1, 2, 3); σ = 35 + 42k (k = 1, 2)
ν = 6
symmetry = d6 (regular hexagon)

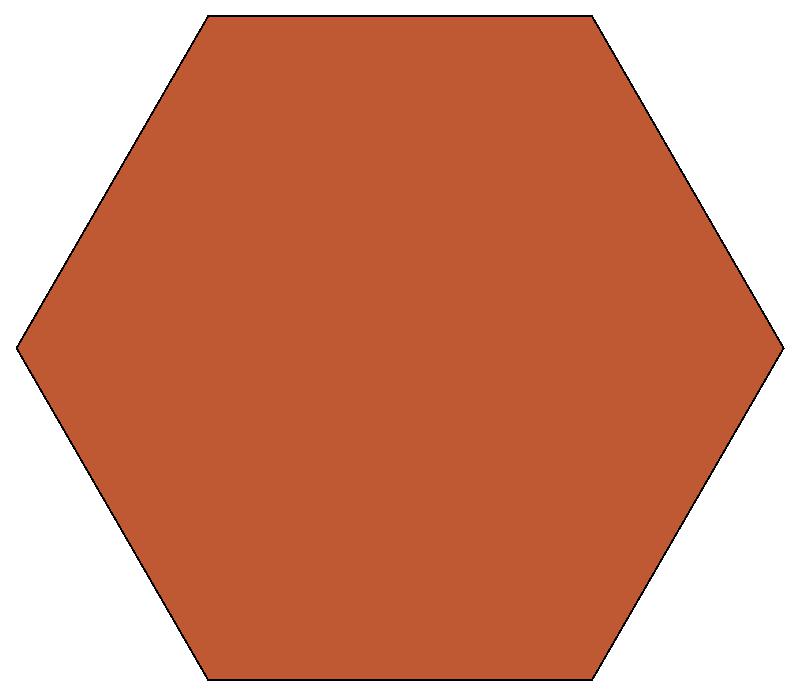
7 49 91 133 175 217 259
287 245 203 161 119 77 35
The σ values in these two rows of
captions are pairwise complementary.

(d)
(n, α) = (147, 3)
σ = 14 + 42k (k = 0, 1, 2, 3); σ = 28 + 42k (k = 0, 1, 2)
ν = 3
symmetry = d3 (equilateral triangle)

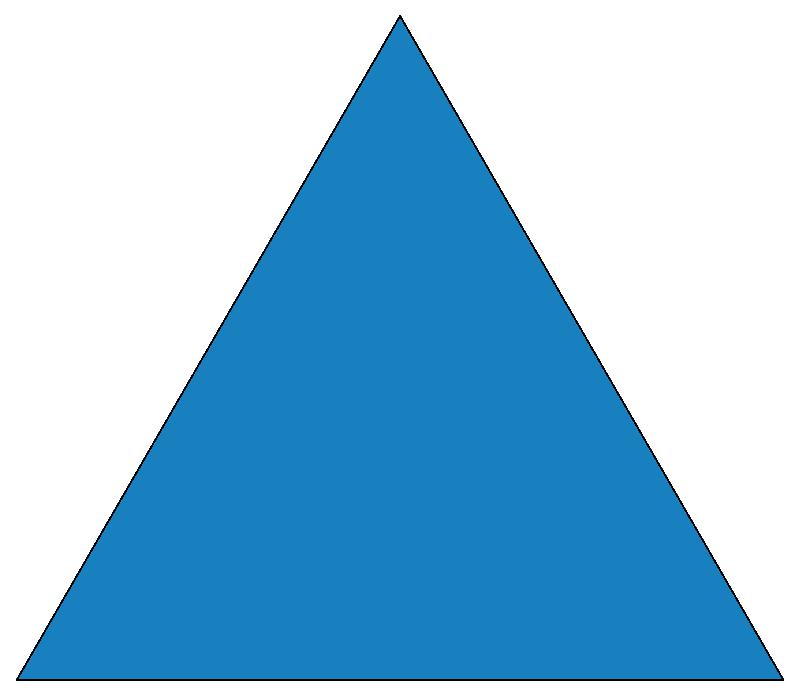
   14 56 98 140 182 224 266
280 238 196 154 112 70 28
The σ values in these two rows of
captions are pairwise complementary.

(e)
(n, α) = (147, 3)
σ = 21k (k = 1, 2, 3, ...)
ν = 1
            symmetry = d2 (horizontal unit line segment)

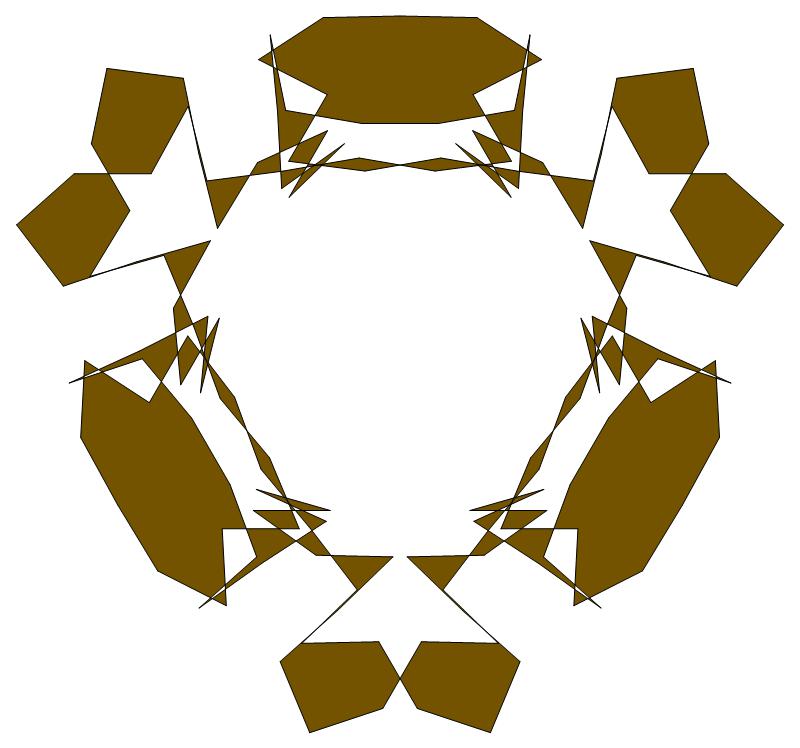
(f)
(n, α) = (147, 3)
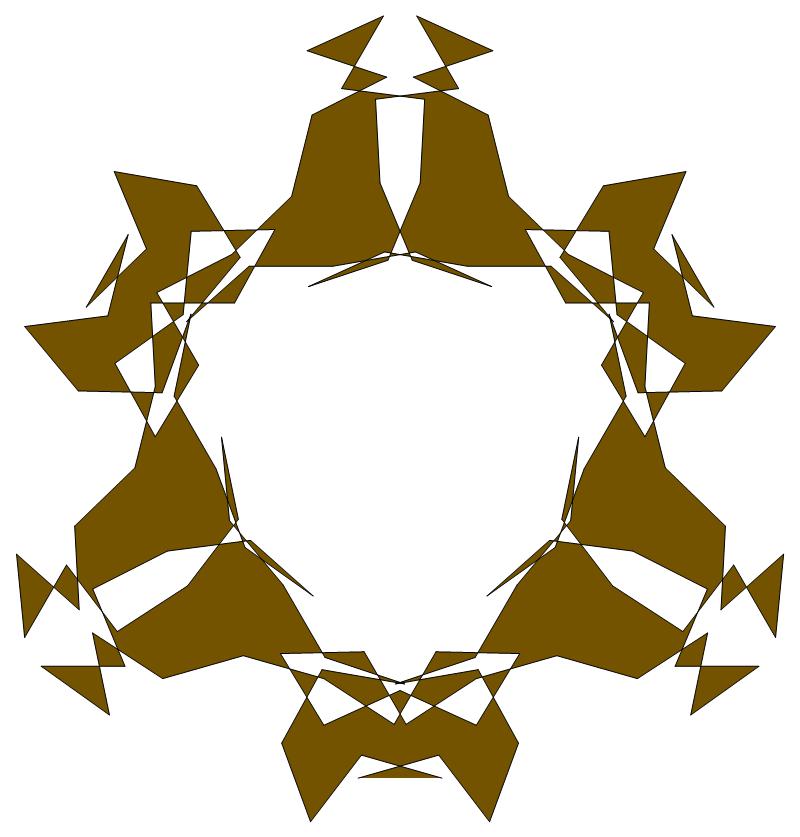
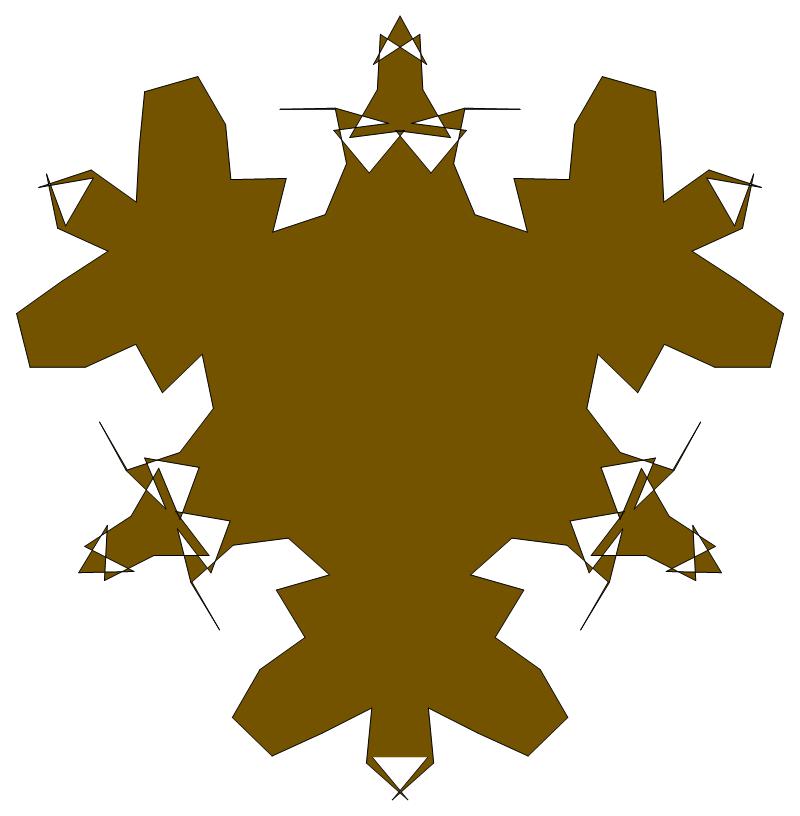
     σ = every even integer divisible by neither 3 nor 7
ν = n
symmetry = d3
There are 14 distinct images, each one
produced by exactly six different values of σ < 2n (=294).
The captions under each image list these six σ values.
The σ values σ₄, σ₅, and σ₆ in the lower captions
   define an 'upside-down' version of the 'rightside-up'
    image defined by σ₁, σ₂ and σ₃. For each of these
         14 images, σ₁ + σ₂ = σ₆ — and (σ₄ + σ₅) mod 294 = σ₃.

2 134 158         4 22 268    8 44 242
   292 160 136         290 272 26    286 250 52

   10 82 202    16 88 190    20 110 164
284 212 92    278 206 104    274 184 130

   32 86 176     34 40 220 38 62 194
      262 208 118      260 254 74    156 132 100

46 106 142    50 116 128       58 64 172
   248 188 152 244 178 166       236 230 122

        68 80 146 76 94 124
           226 214 148    218 200 170

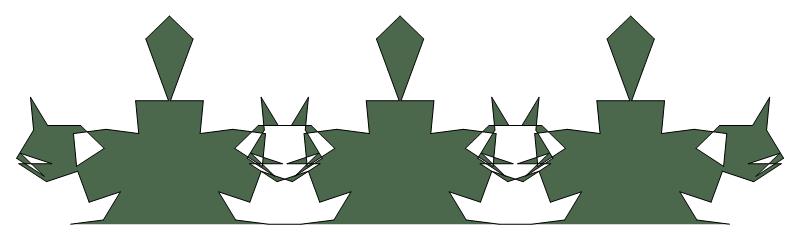
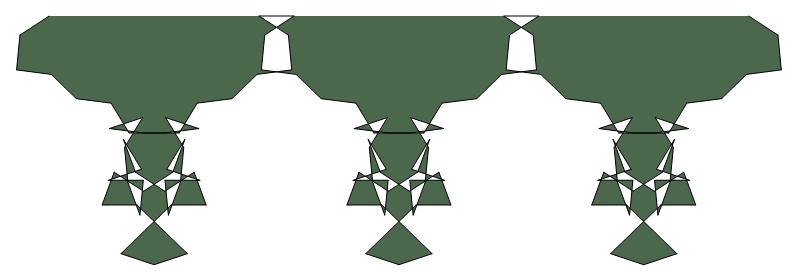
(g)
(n, α) = (147, 3)
    σ = integer i that is divisible by 6 but not by 42
ν = n
symmetry = lattice
There are 7 distinct images, each produced
by precisely six different values of σ < 2n (= 294).

The σ values in these two rows of
captions are pairwise complementary.

6 108 180       12 66 216       18 30 246
288 186 114    282 228 78    276 264 48

24 132 138       36 60 198      54 90 150
   270 162 156   258 234    96        240 204 144

       72 102 120
           222 192 174

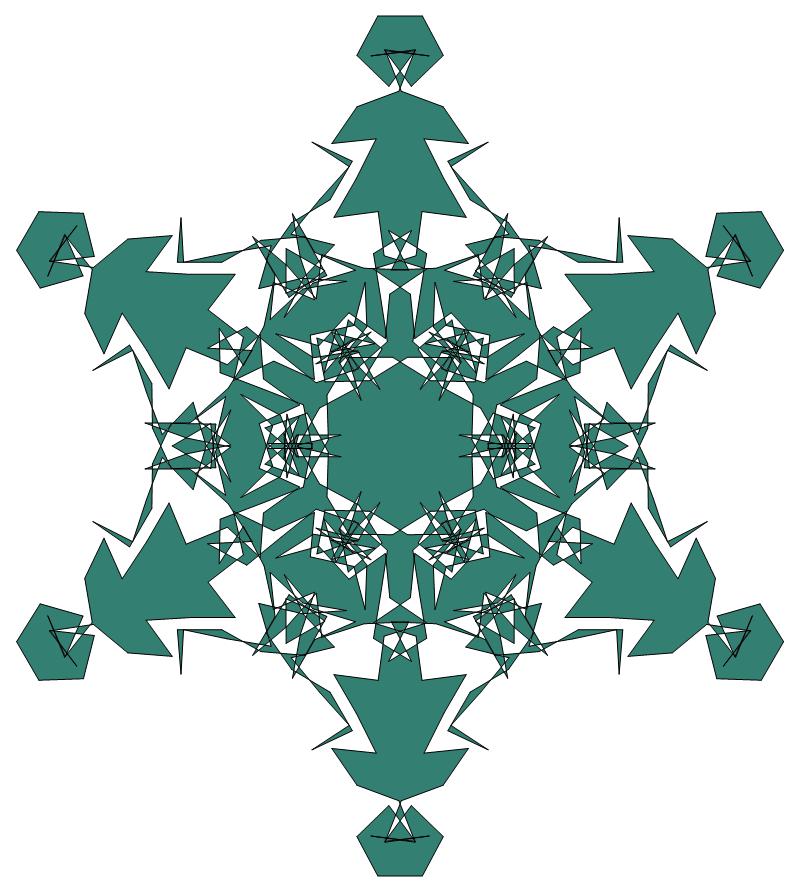
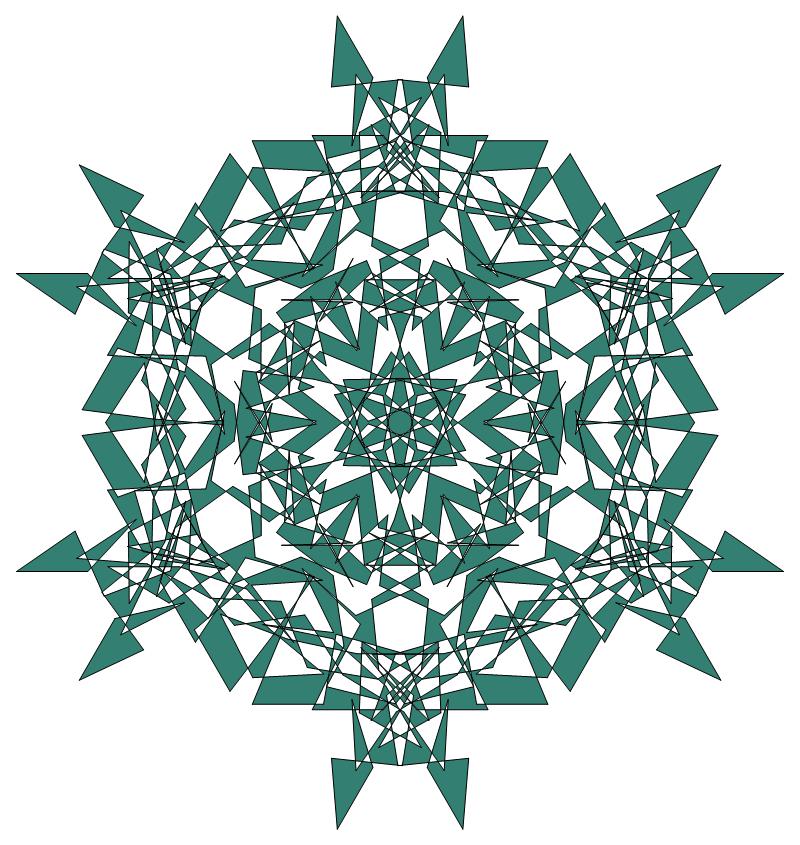
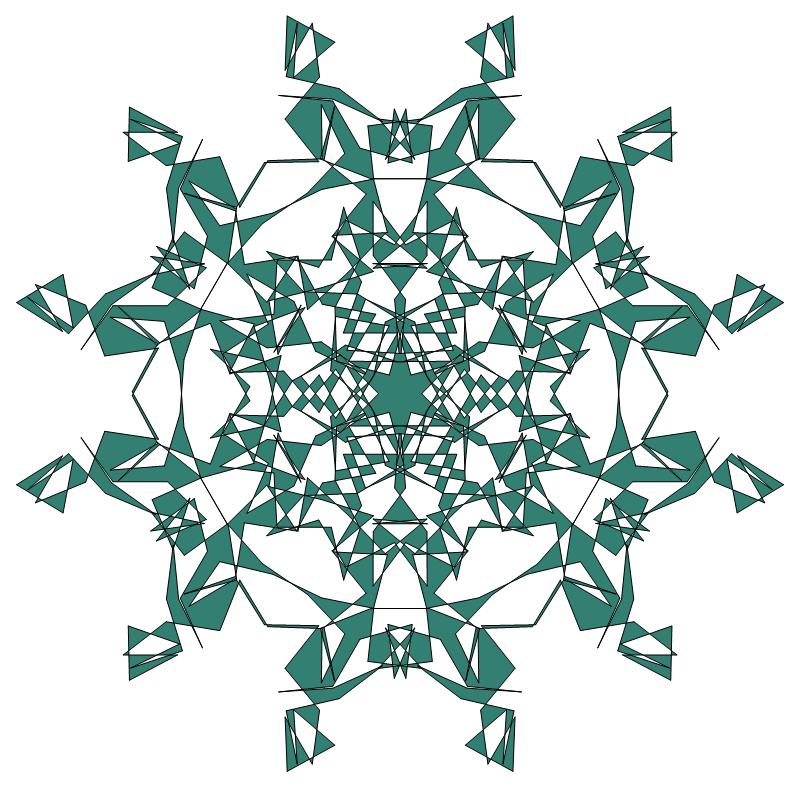
EXAMPLE: (n, α) = (3 ⋅ 11², 3)
= (363, 3)
(a)
   σ = every odd integer i ∋ GCD(i, n) = 1
ν = n
symmetry = d6
There are 121 distinct images.
The label under each image lists its σ value.

1    5    7

13        15    17

19        23    25
29        31    35

37     41    43

47     49    53

59           61    65

      67       71         73

79        83       85

89        91       95

    97       101    103

107           109    113

      119       125         127

131        133       137

139        145       149

    151       155    157

161           163    167

      169       173         175

179        181       185

193        197       199

203       205    211

215           217    221

      227       229         233

235        239       245

247        251       257

    259       265    269

271           277    281

      283       287         289

293        295       299

301        305       307

311        313       317

323        325       329

335        337       343

347        349       353

355        359       361

(b)
(n, α) = (363, 3)
   σ = every even integer i ∋ GCD(i, n) = 1
ν = n
symmetry = d3
There are 114 distinct images.
   The label under each image lists its σ value.


2        4          8

   10          14          16

      20        26          28

      32        34          38

      40        46          50

52        56       58

62        64       68

70        74       76

80        82       86

92        94       98

100        104       106

112        116       118

122        124       128

130        134       136

140        142       146

148        152       158

160        164       166

170        172       178

182        184       188

190        194       196

200        202       206

208        212       214

218        224       226

230        232       236

238        244    263.3;    248

250        254       256

260        262       266

268        272       274

278        280       284

290        292       296

298        302       304

310        314       316

320        322       326

328        332       334

338        340       344

346        350       356

358          362

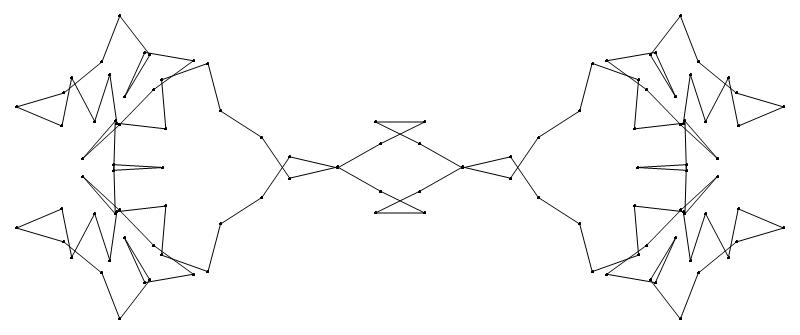
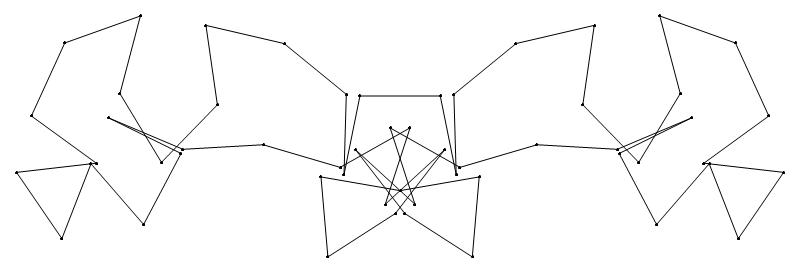
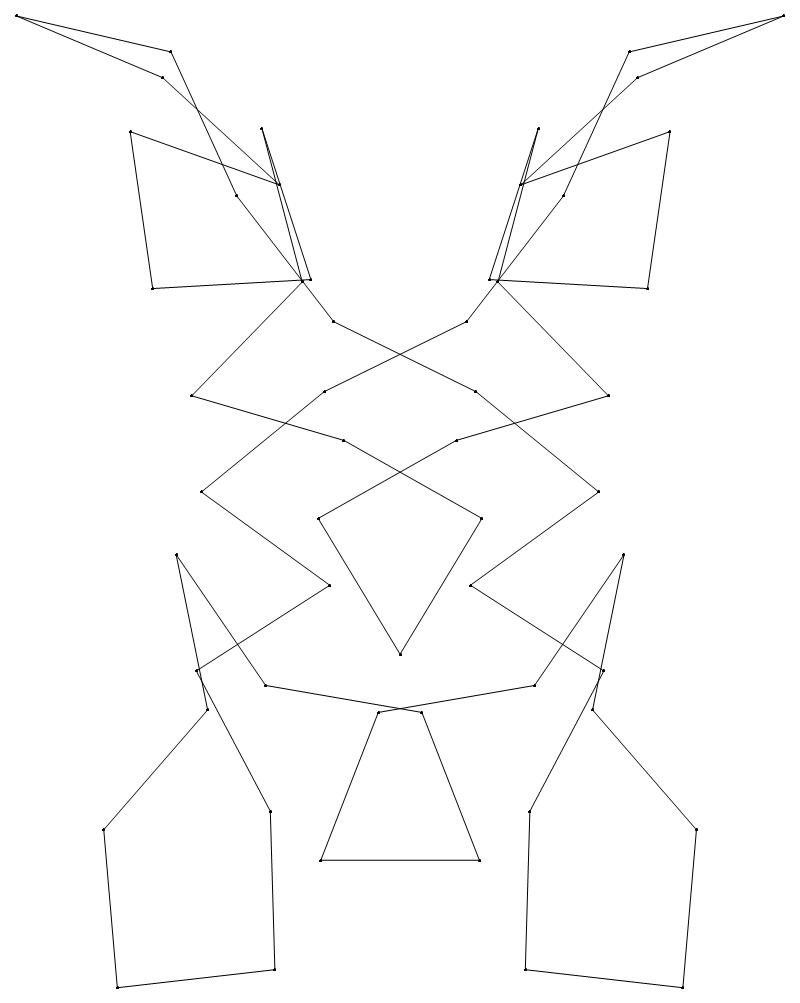
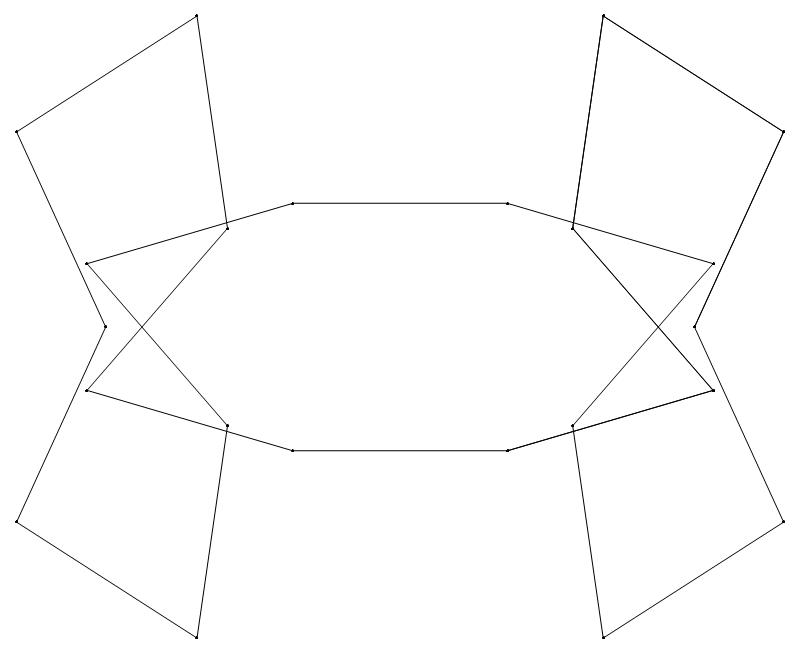
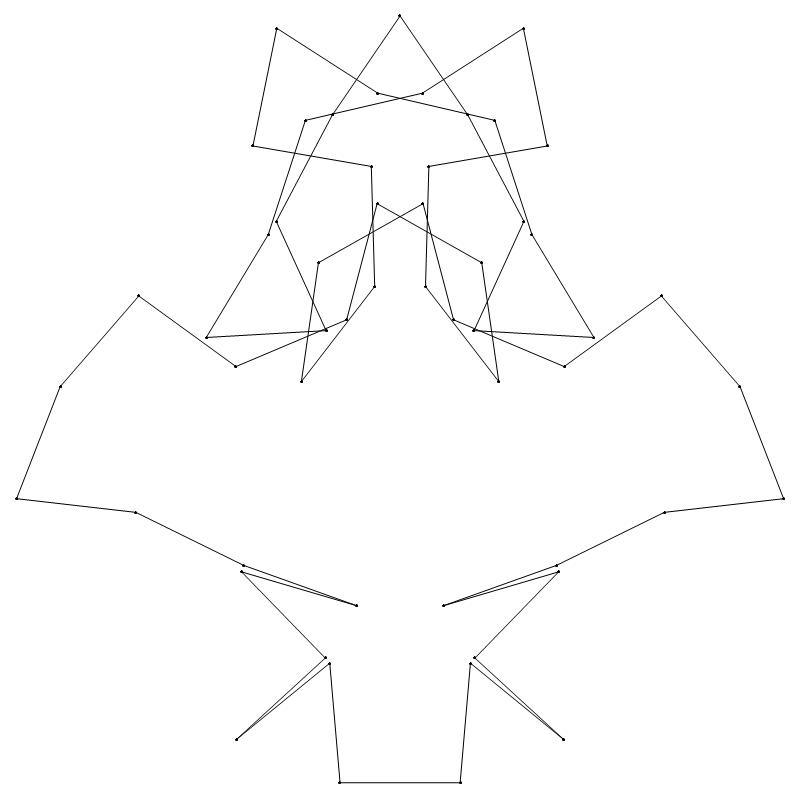
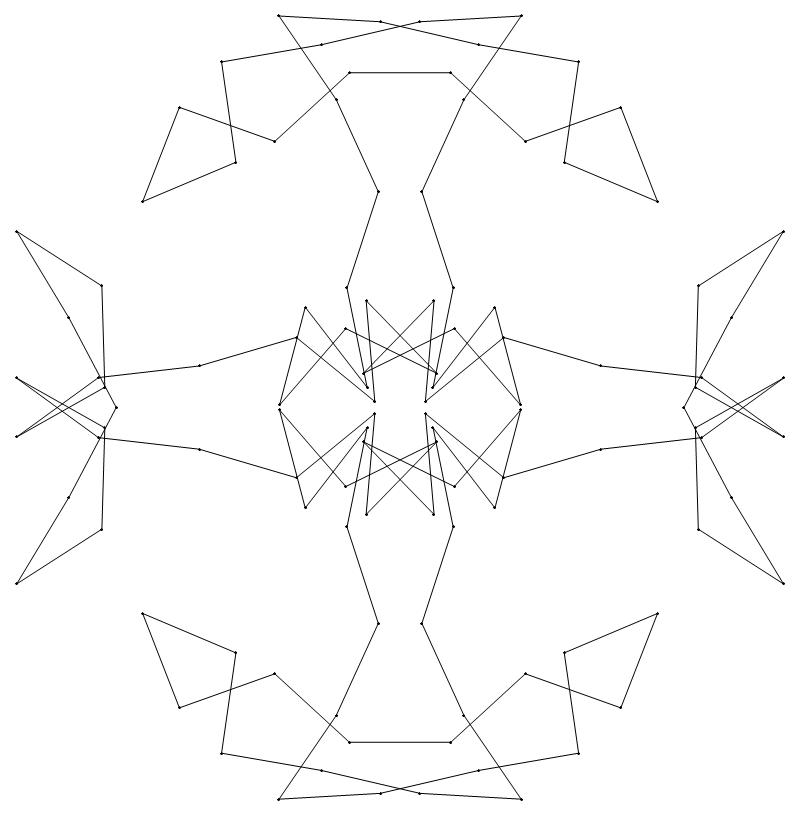
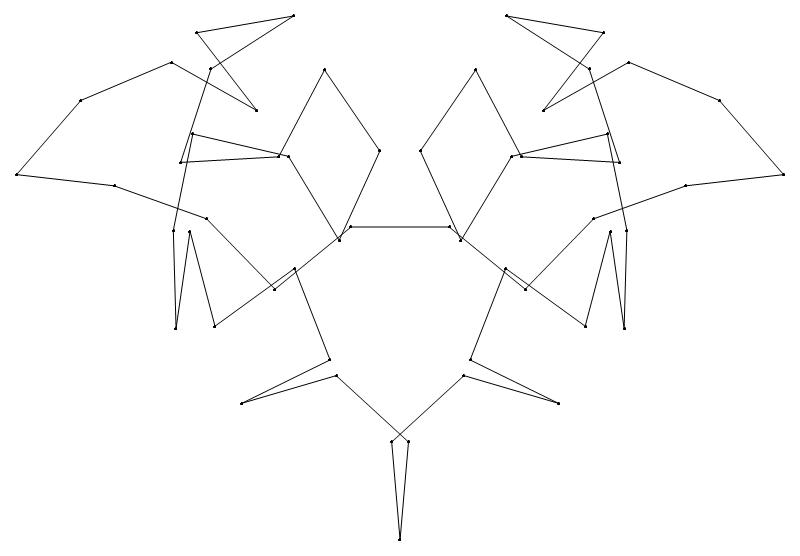
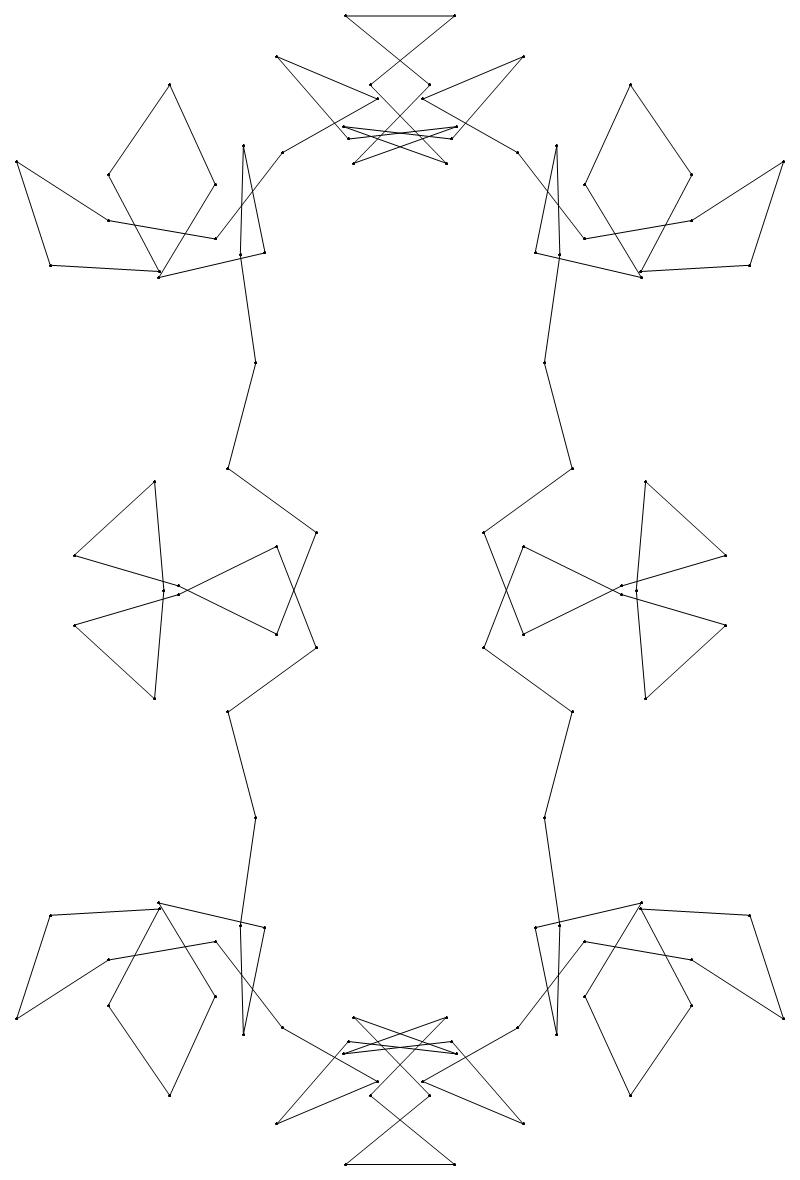
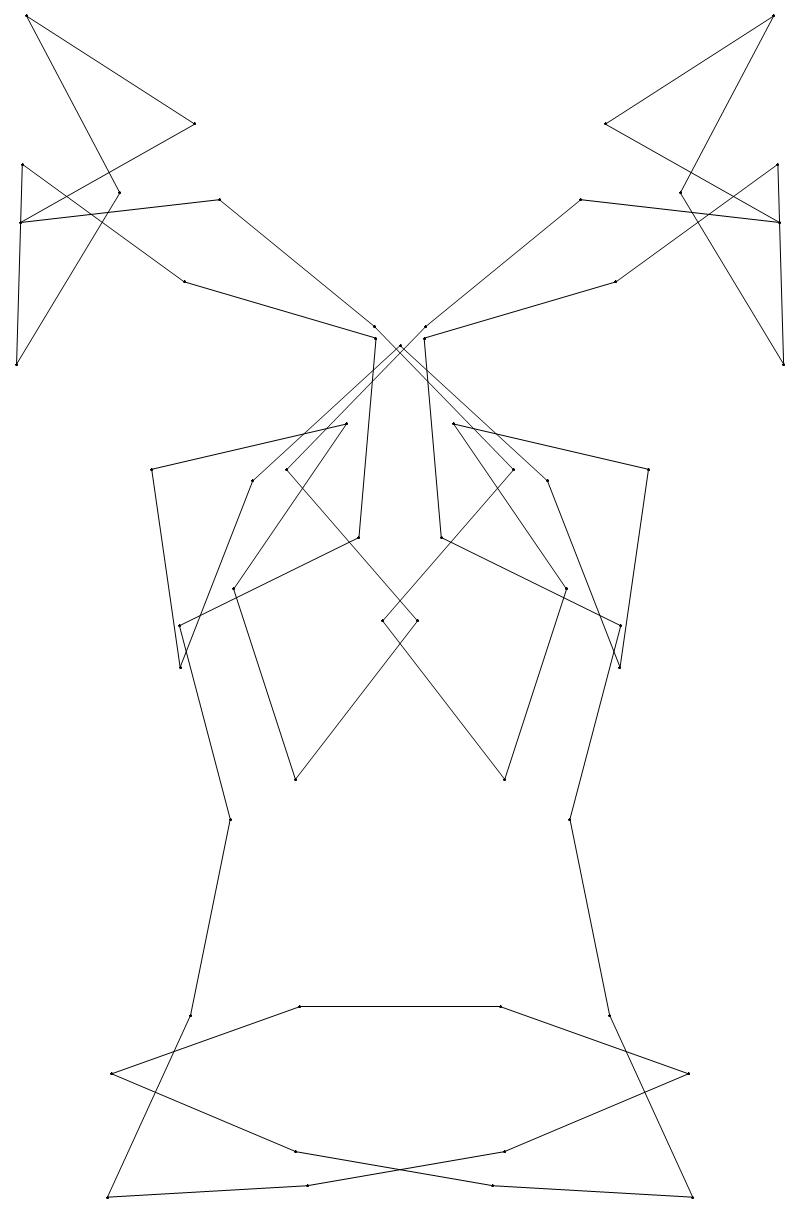
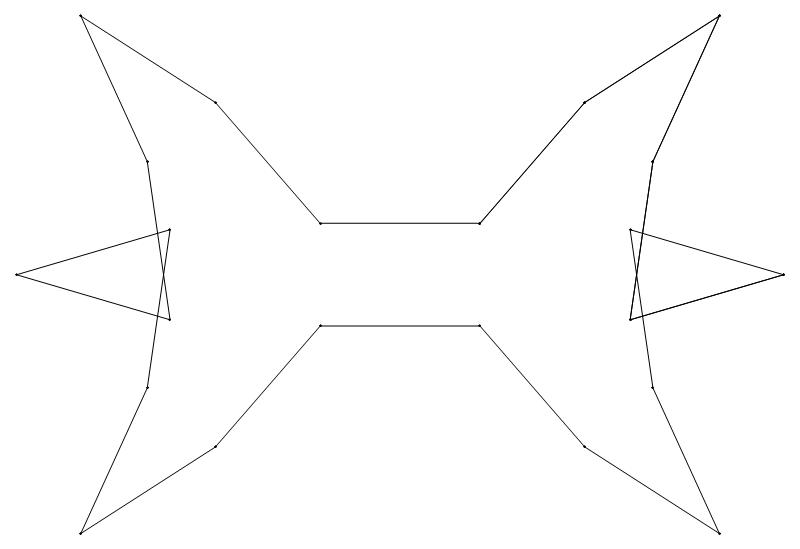
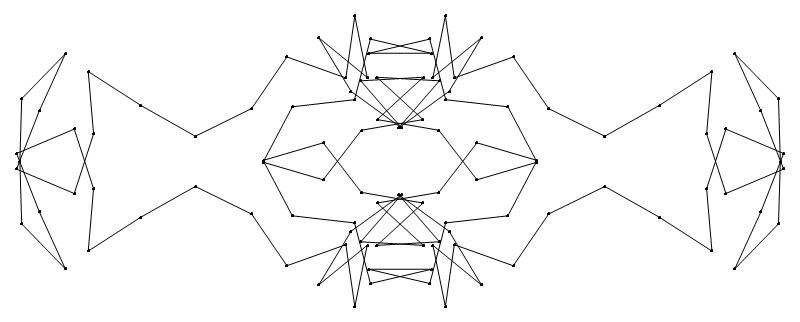
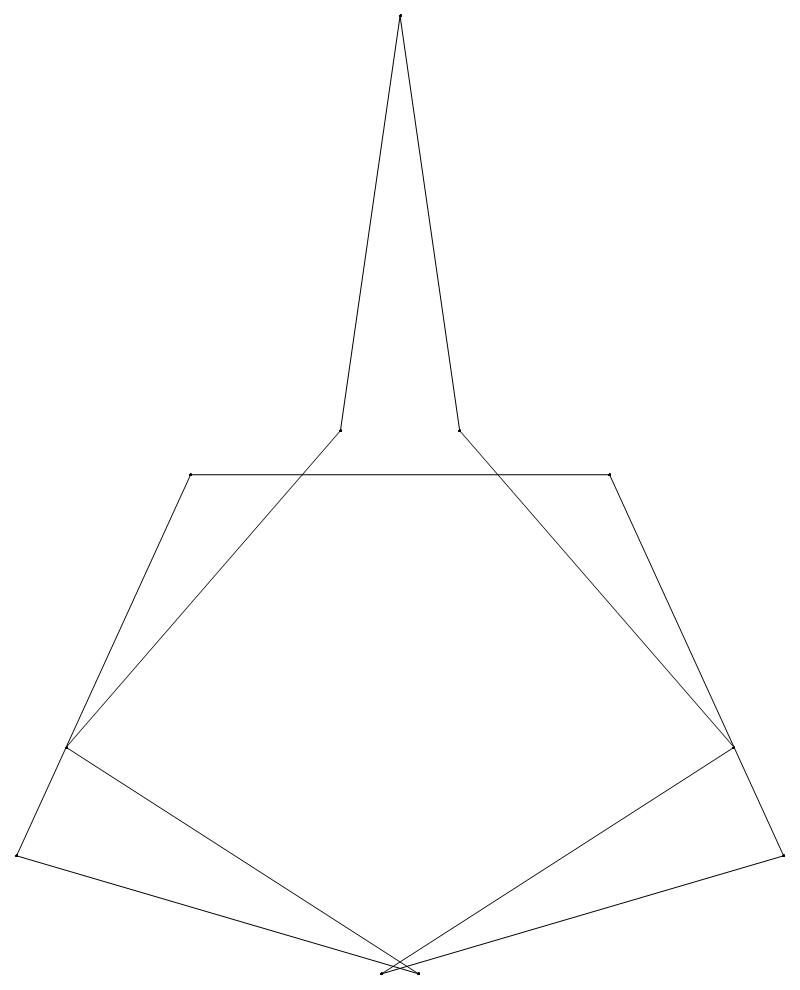
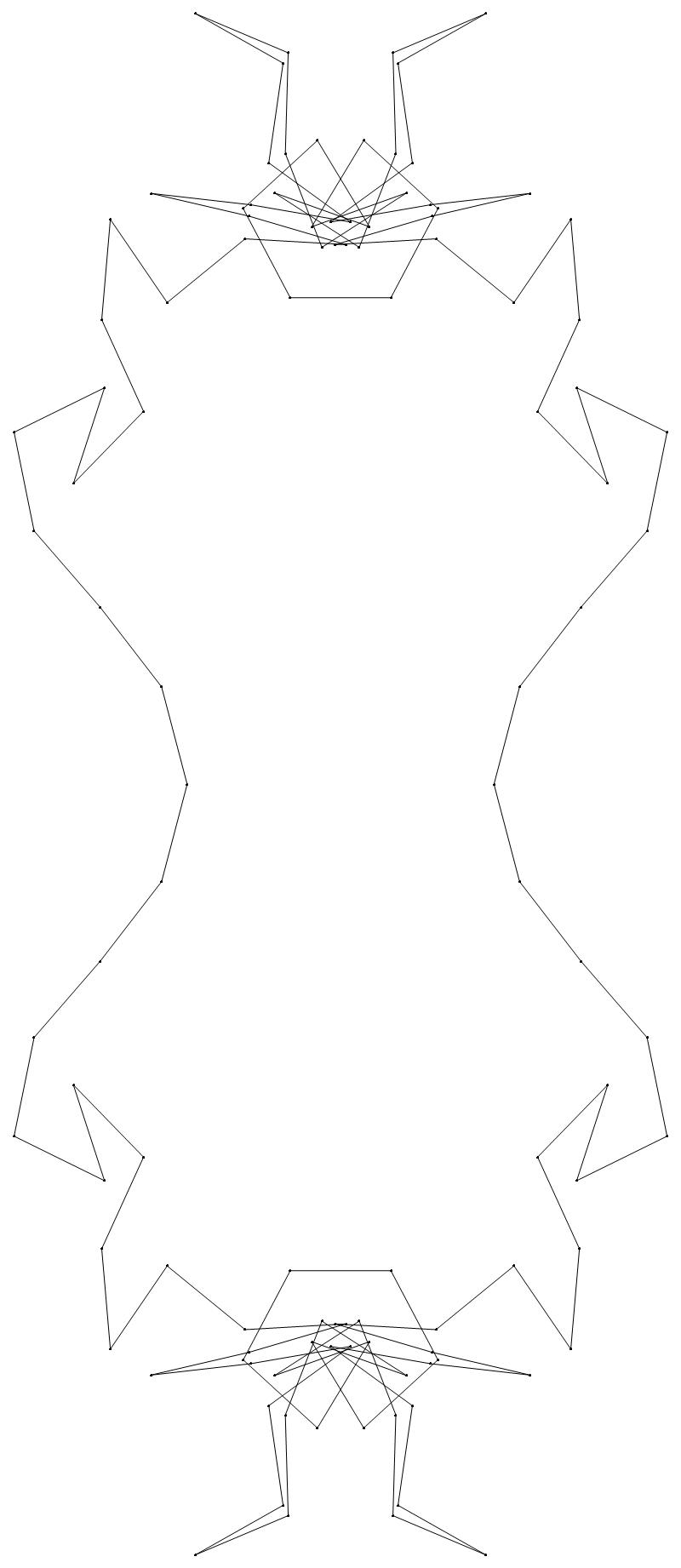
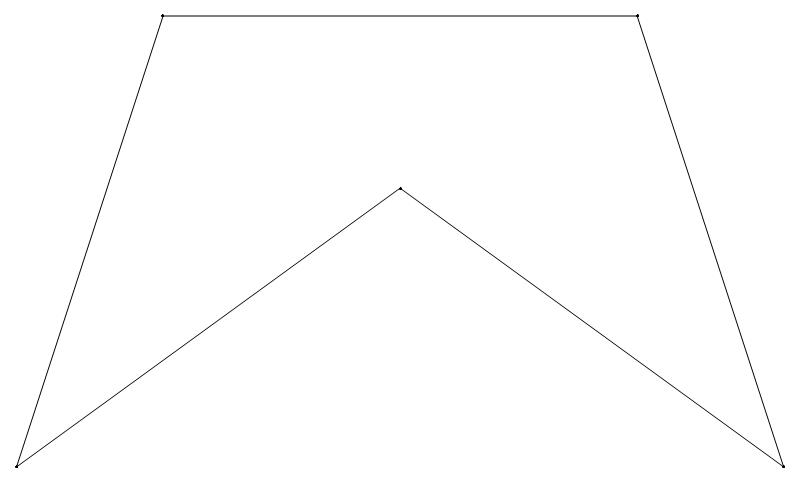
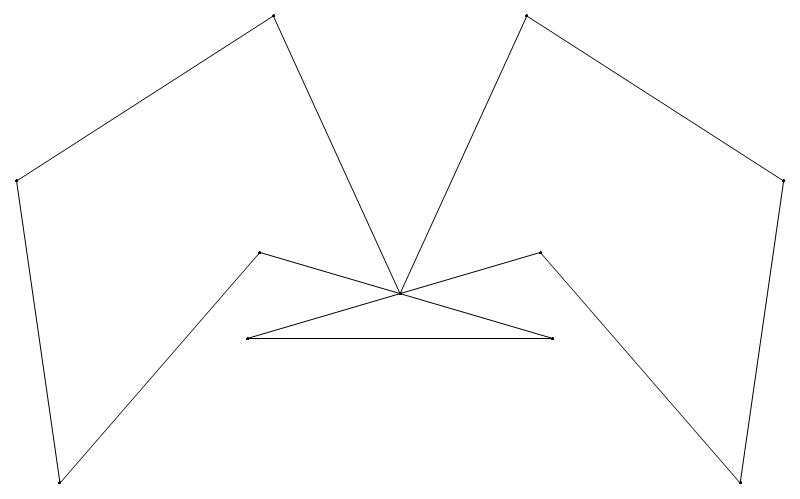
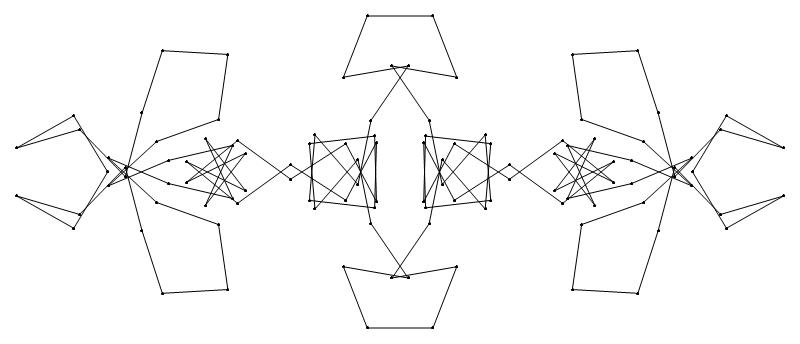
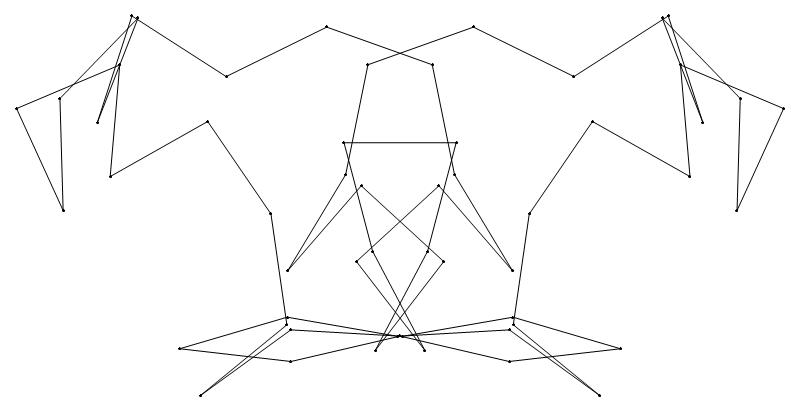
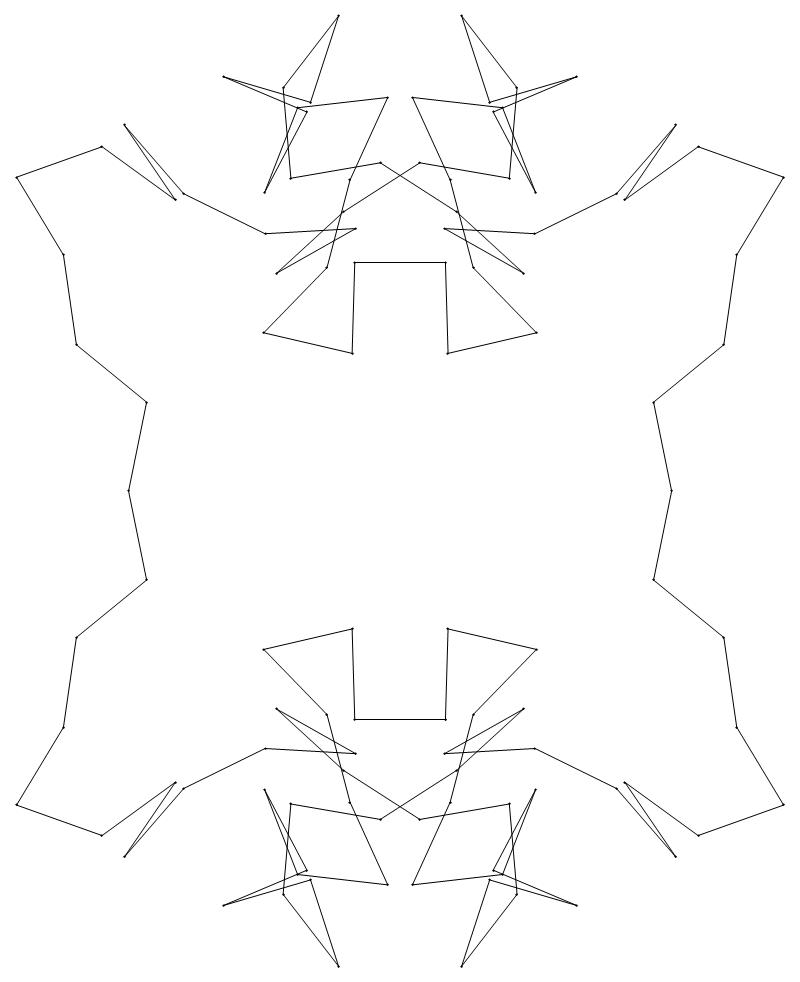
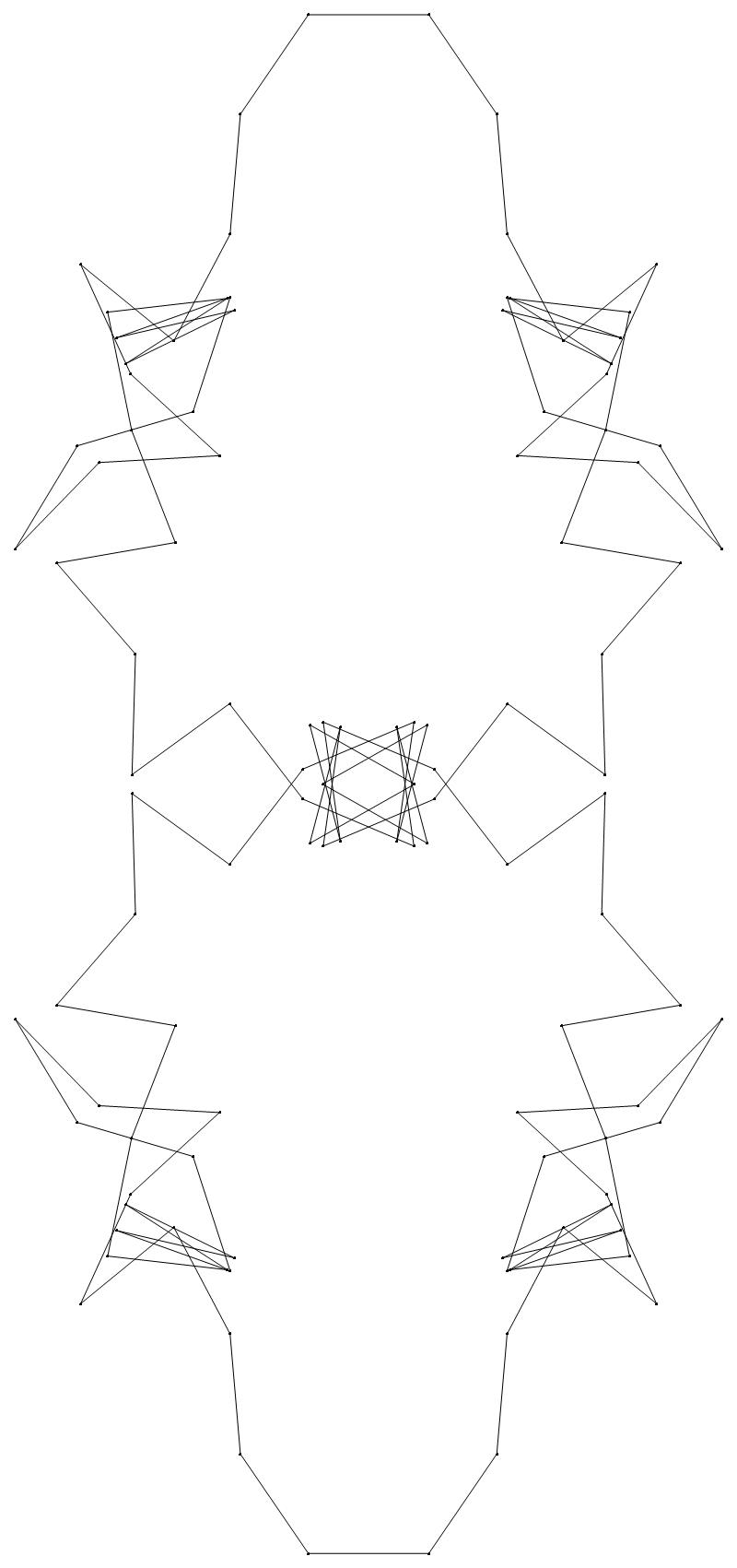
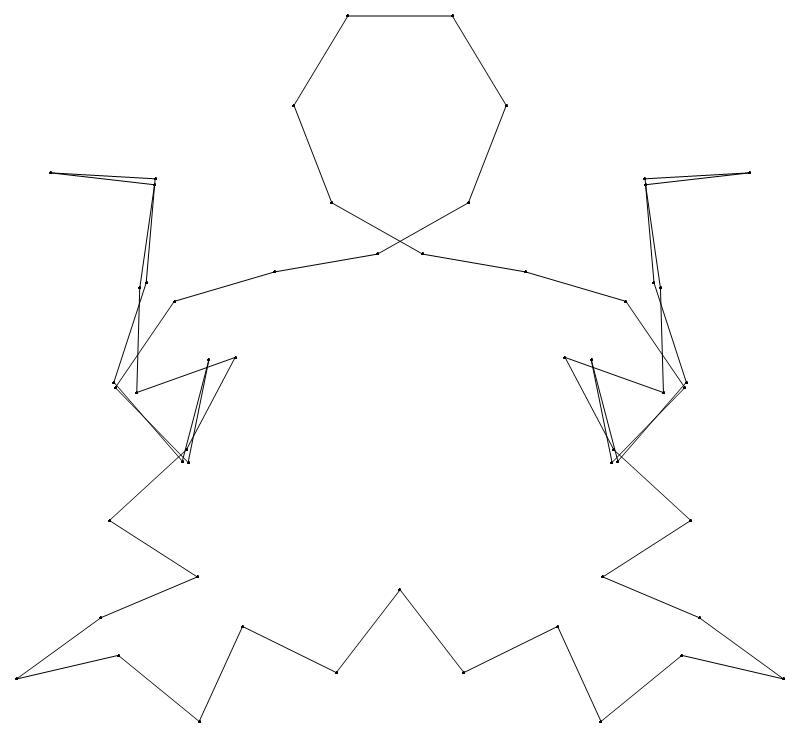
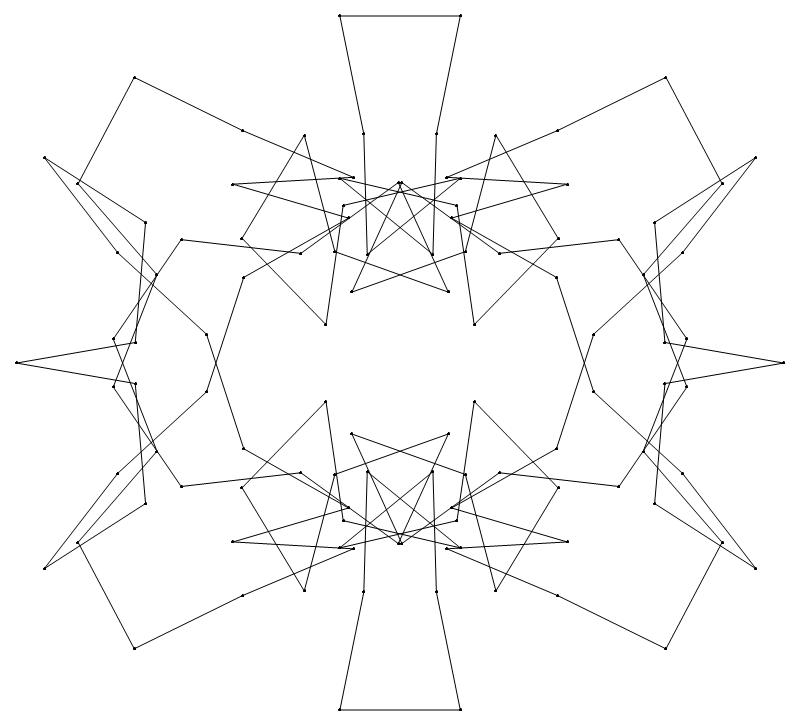
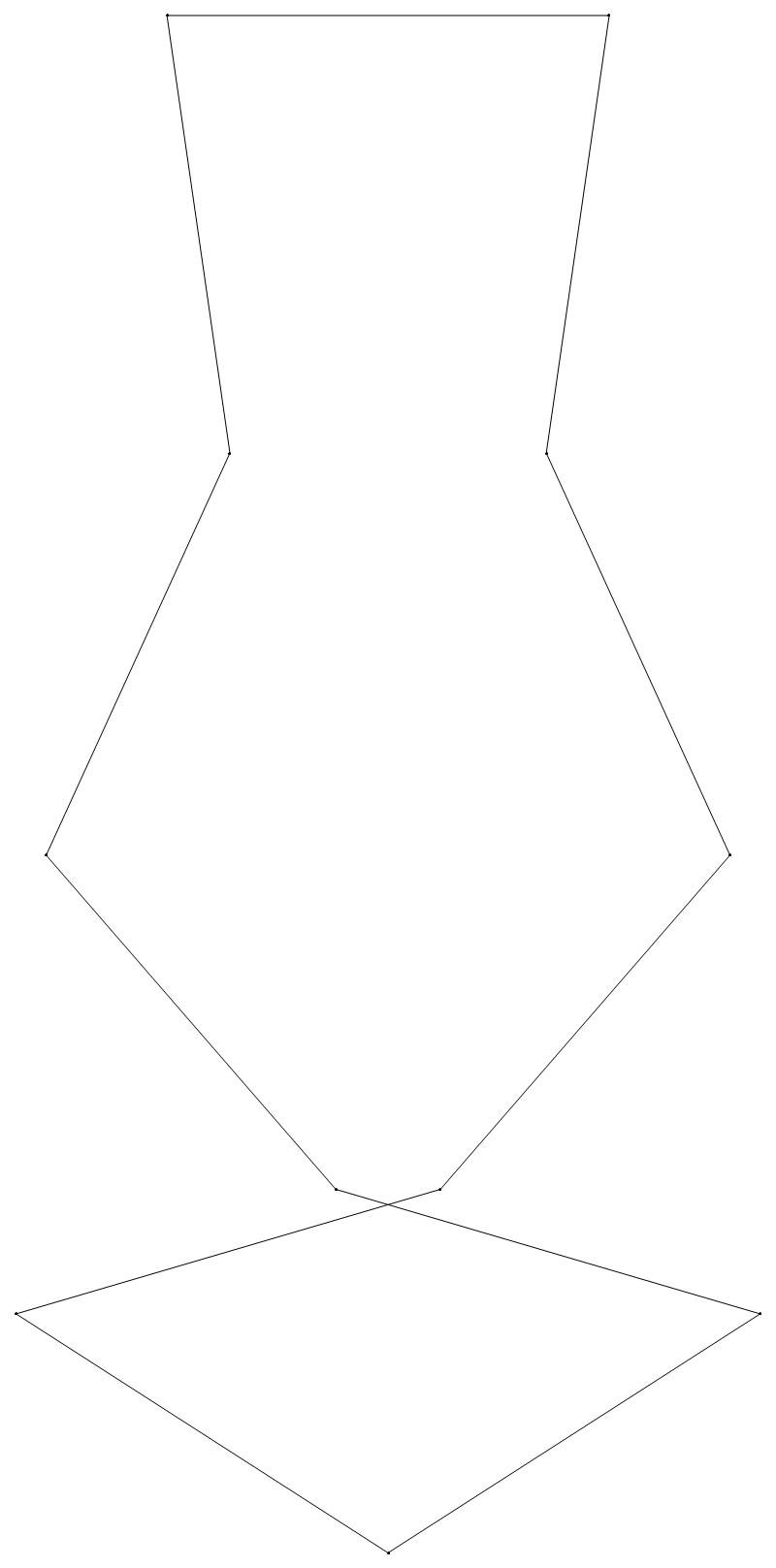
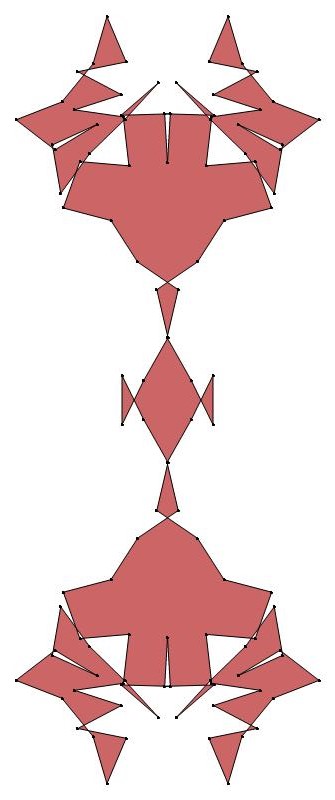
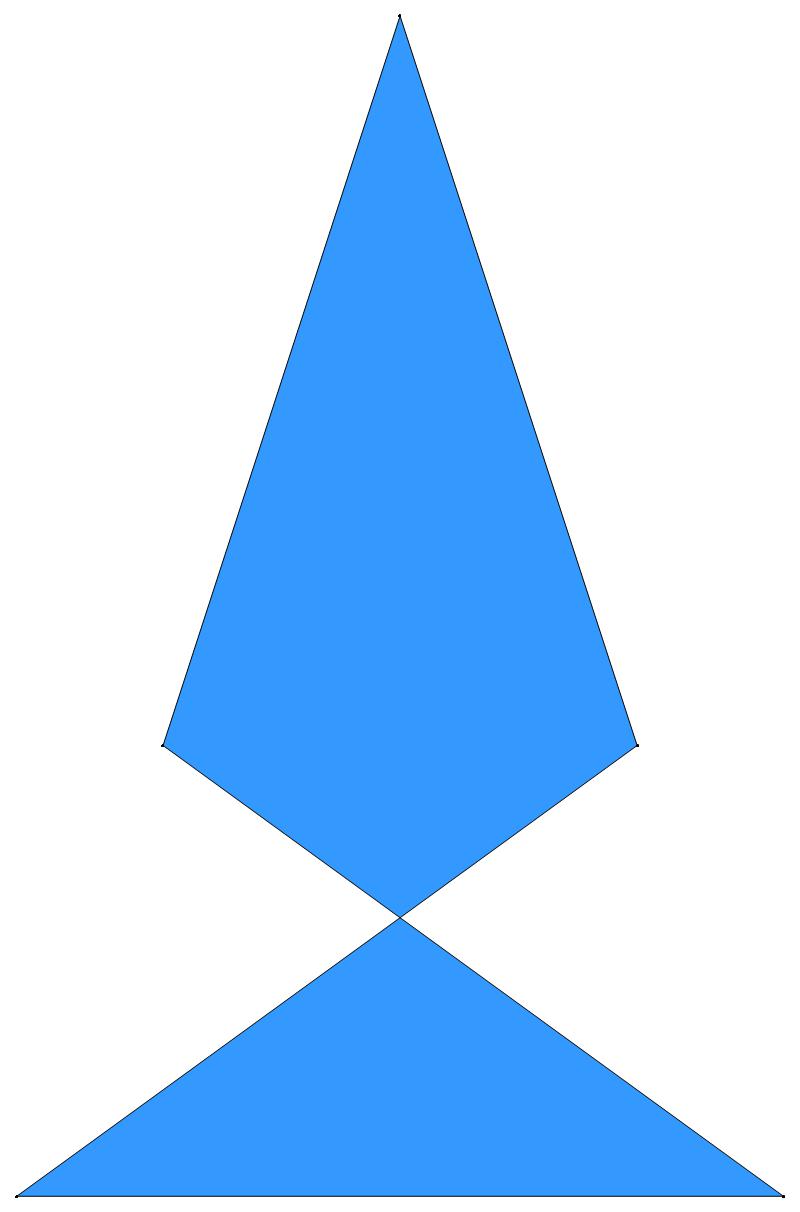
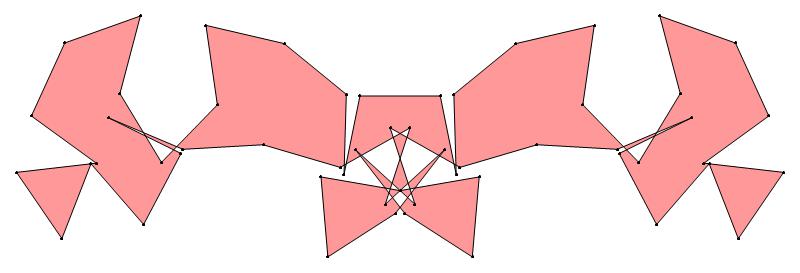
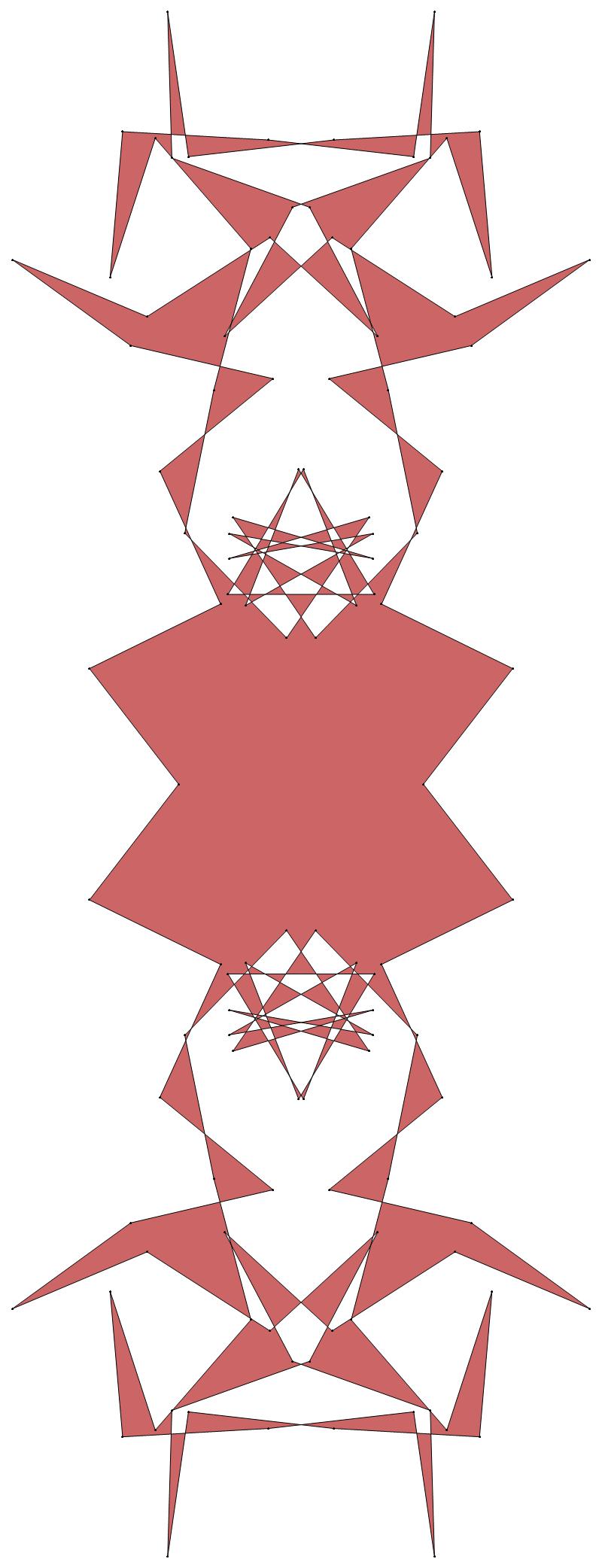
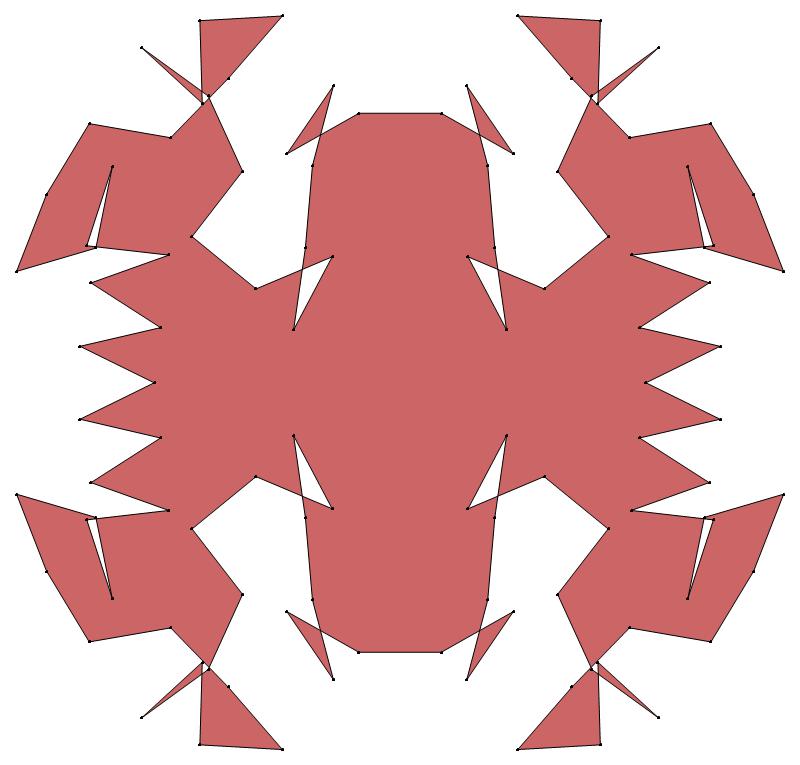
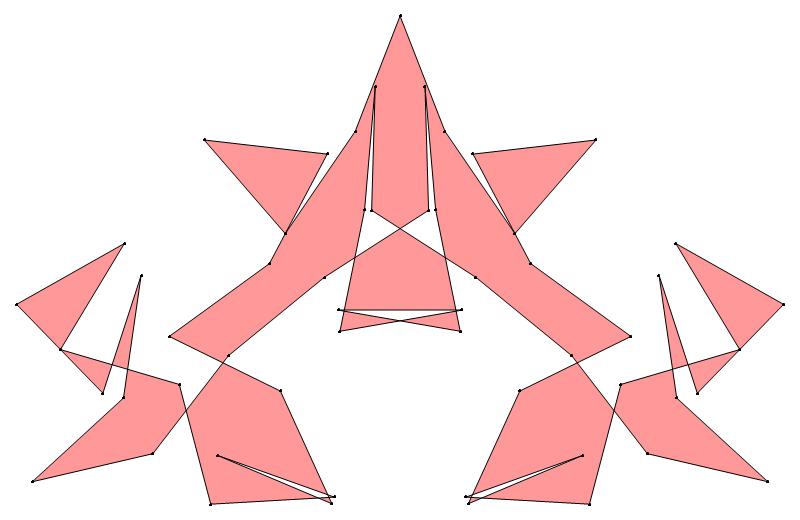
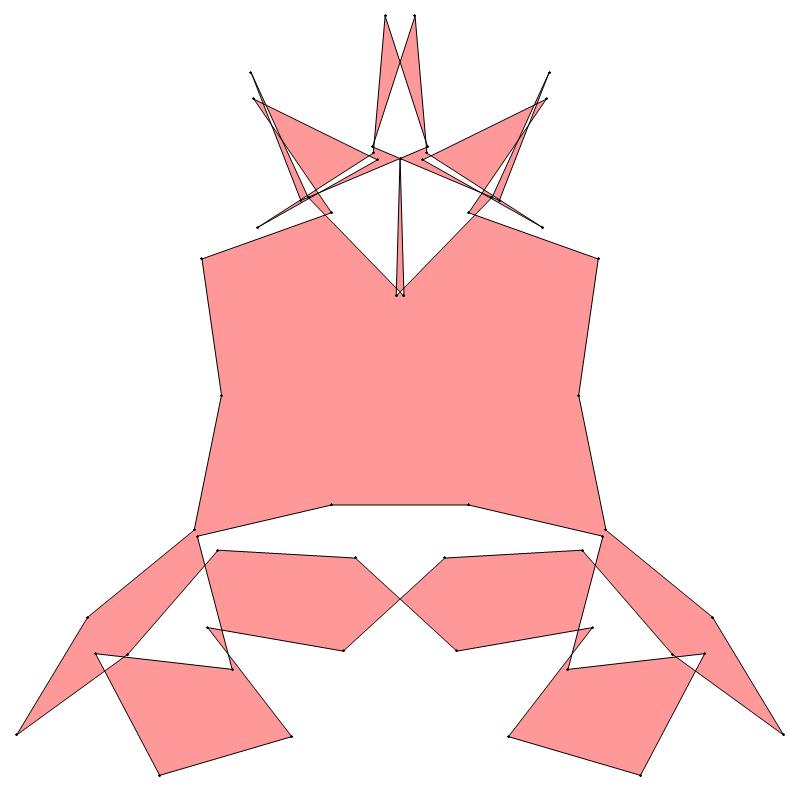
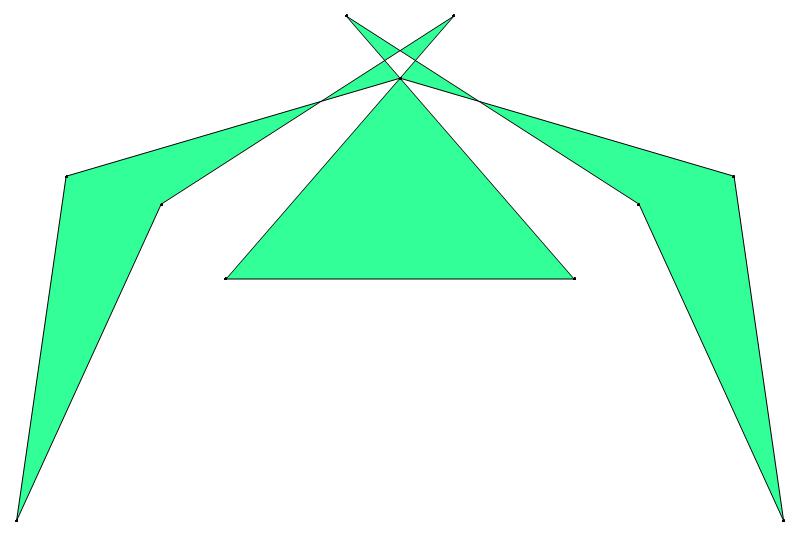
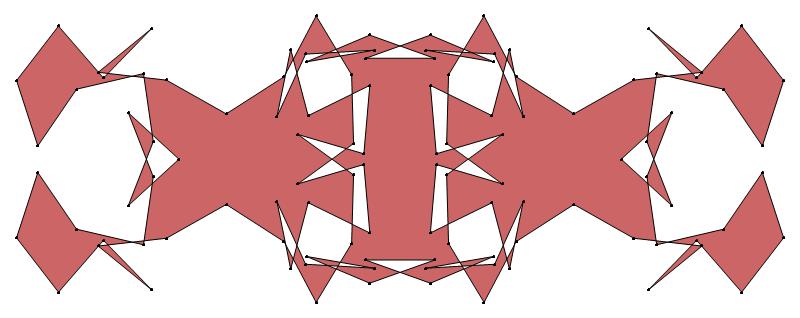
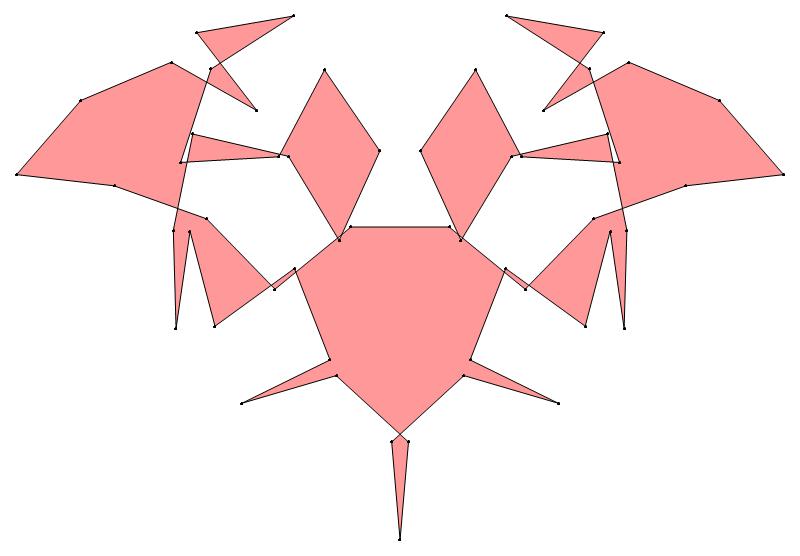
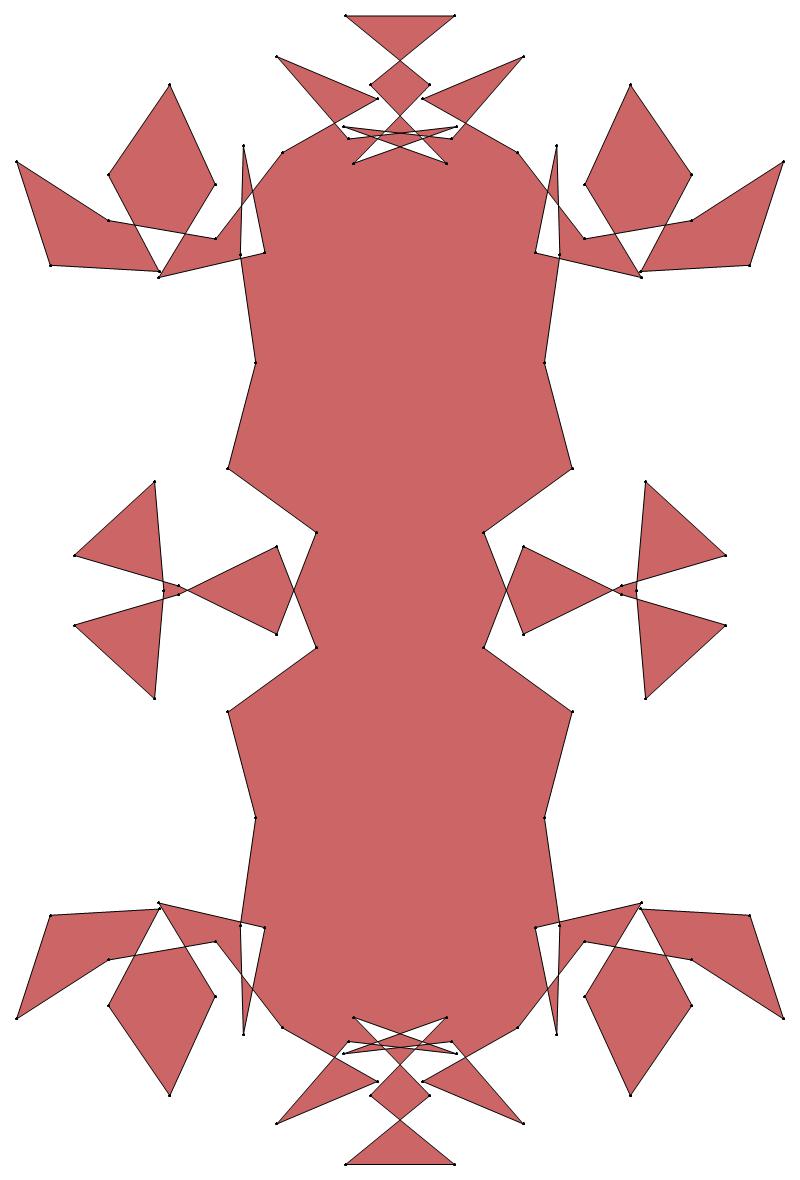
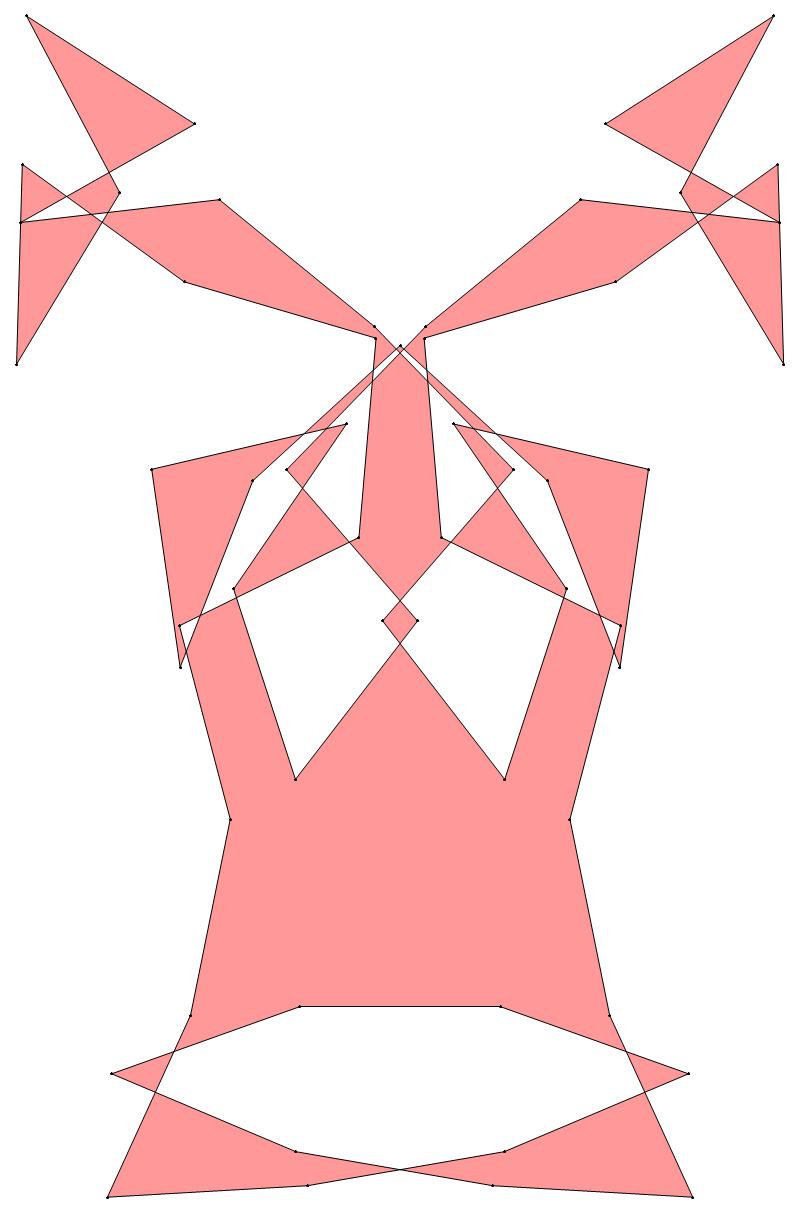
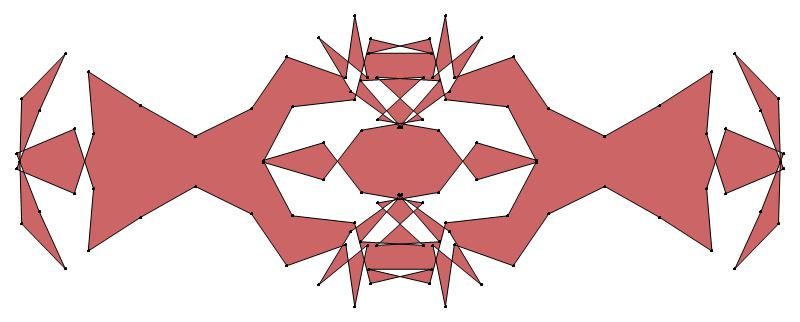
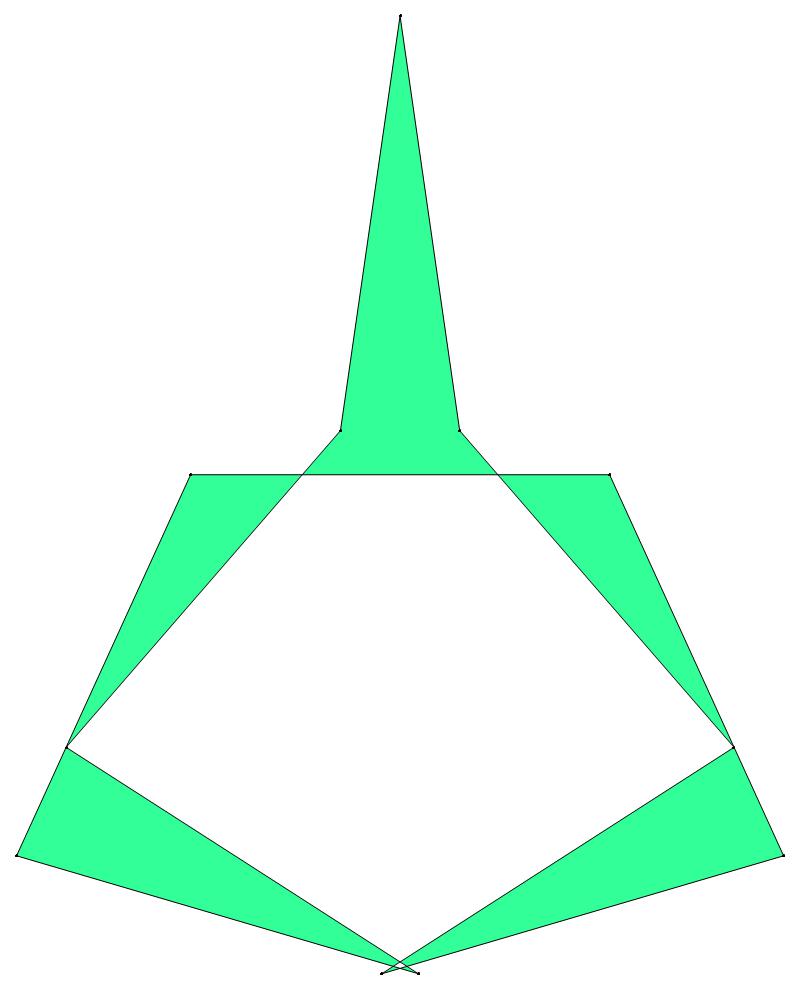
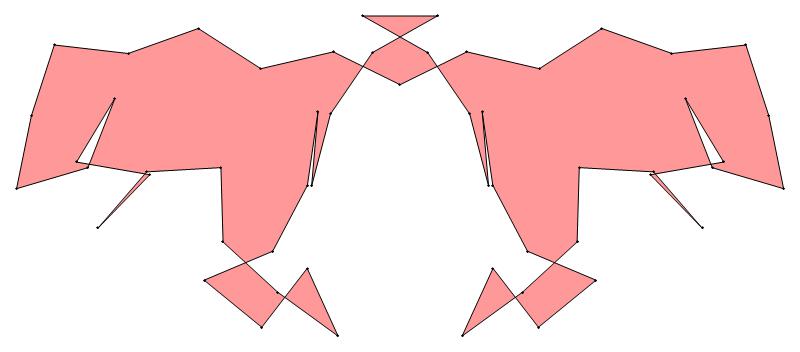
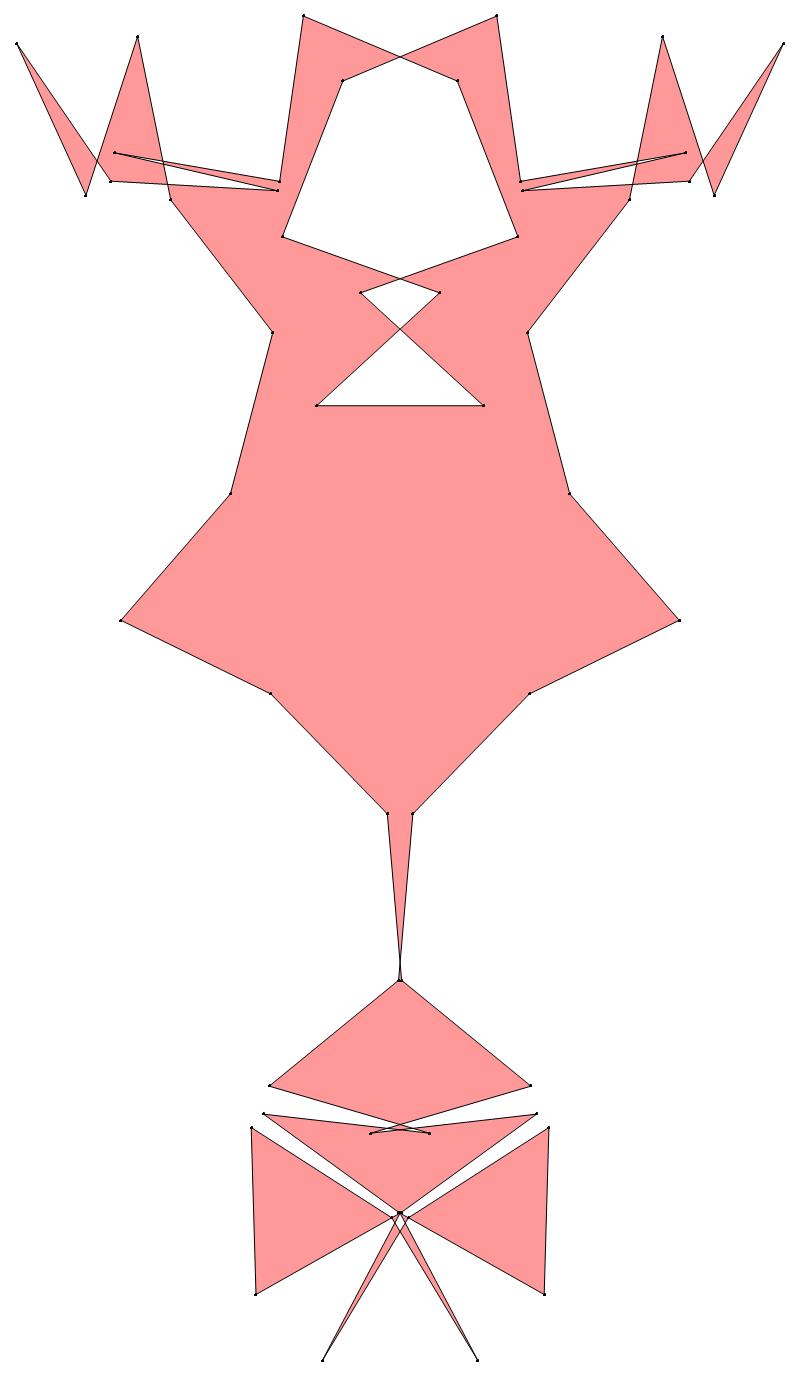
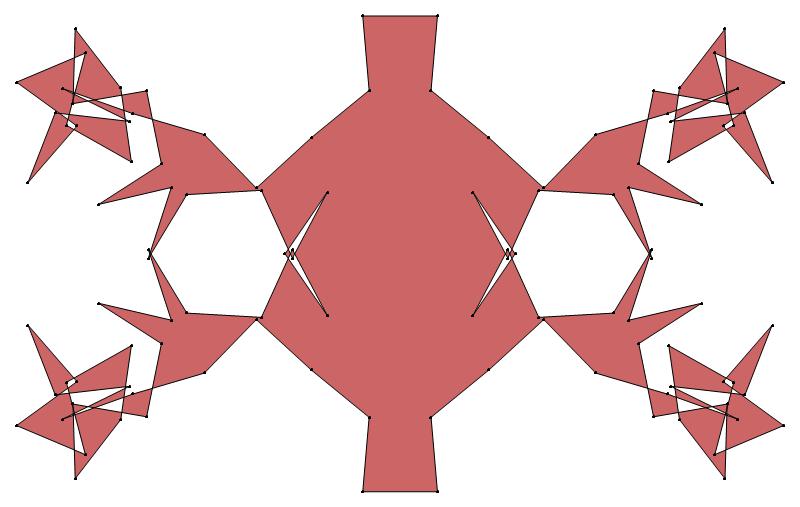
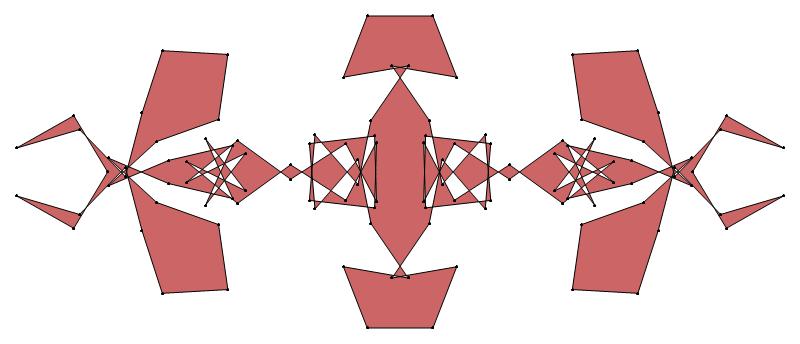
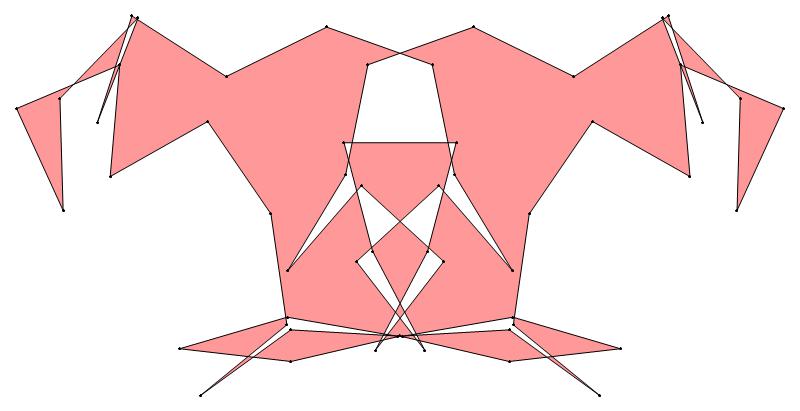
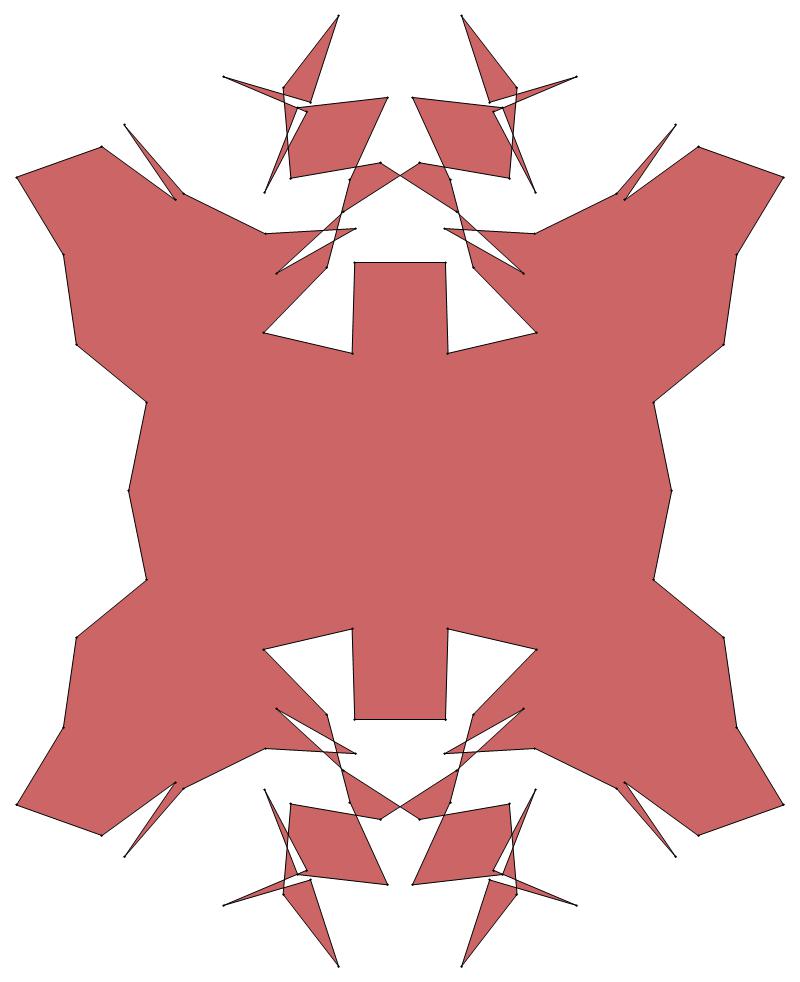
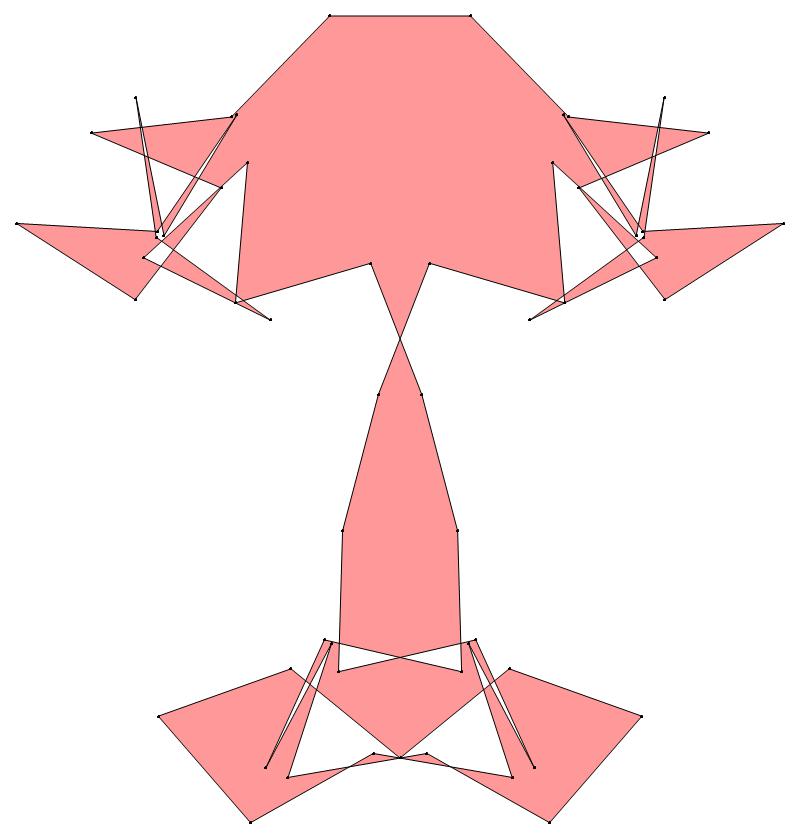
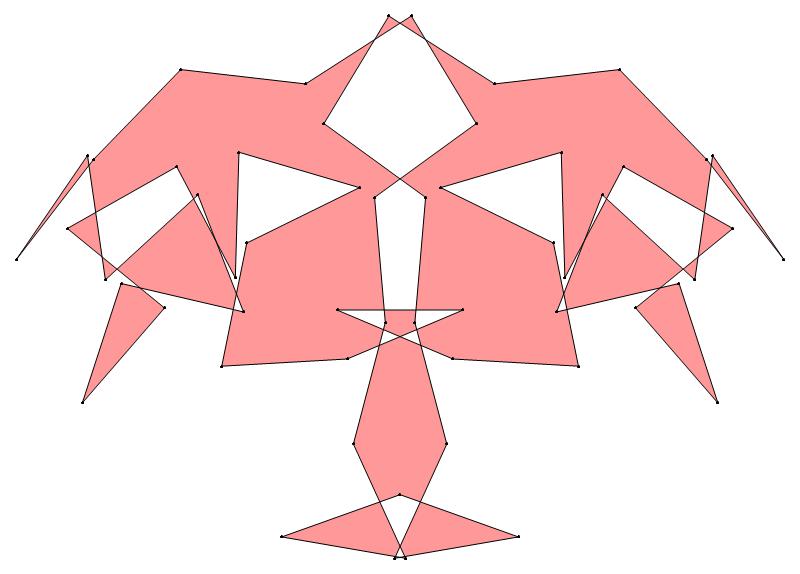
EXAMPLE: (n, α) = (55, 3)
The value of σ = r + 9(c − 1), where
r = row number and c = column number.
Rows are numbered 1 to 9 from bottom to top.
Columns are numbered 1 to 6 from right to left.
(a) b & w
(i) rounded

(ii) standard

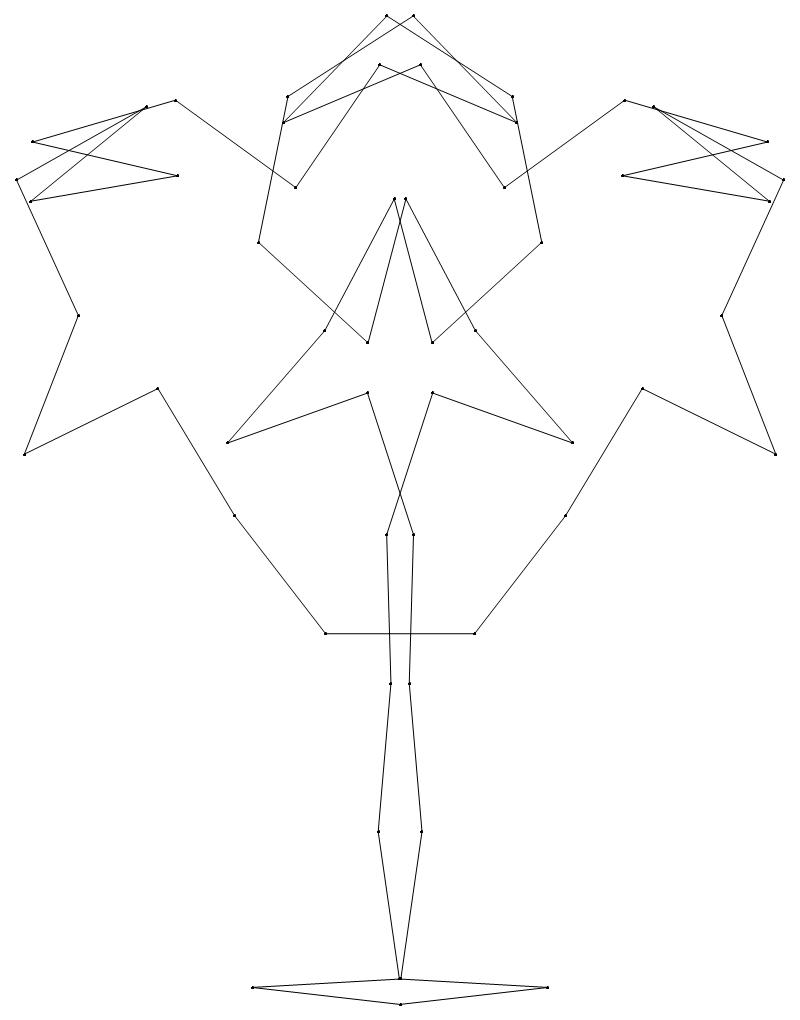
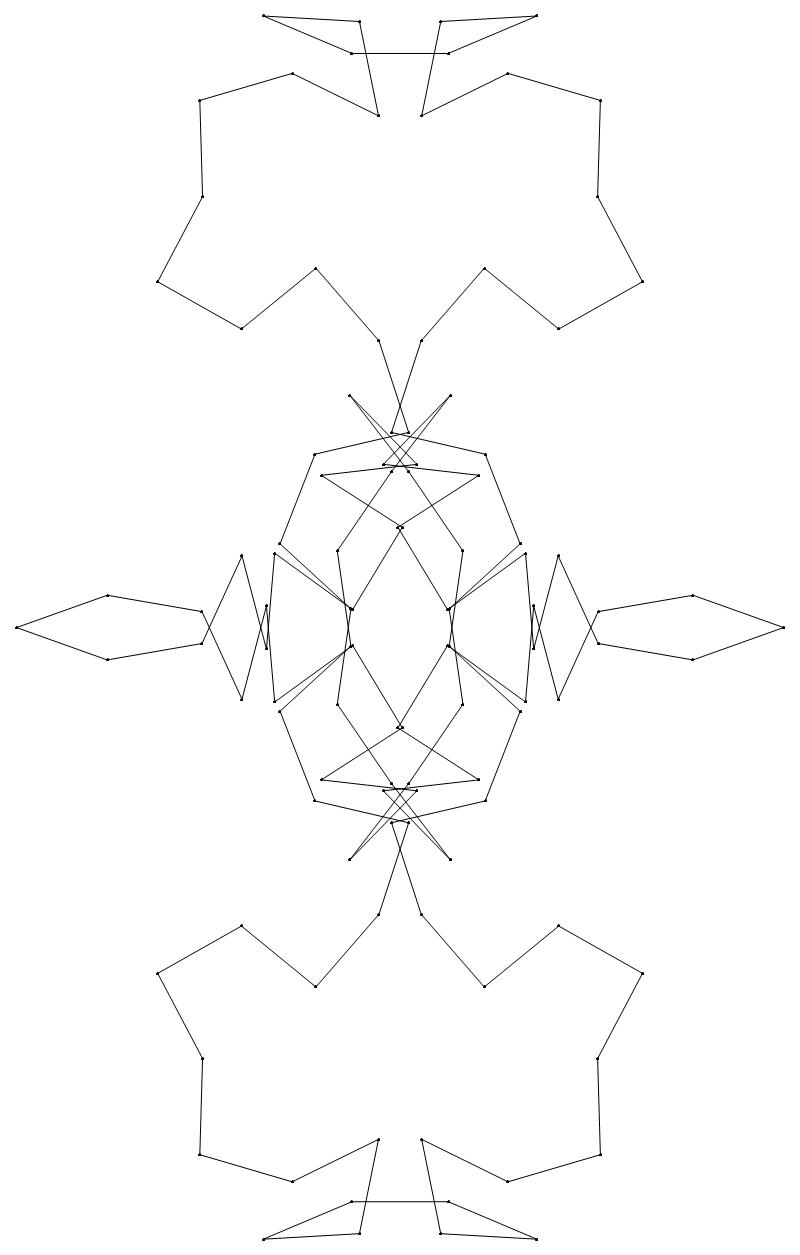
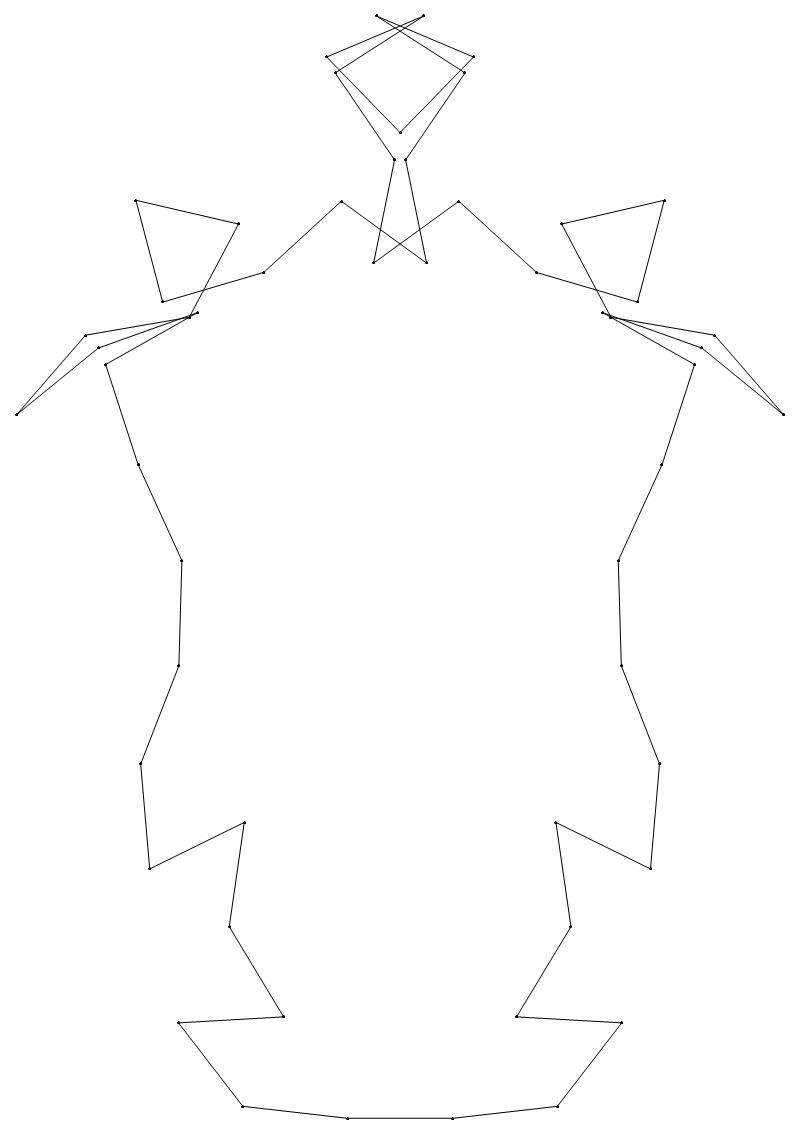
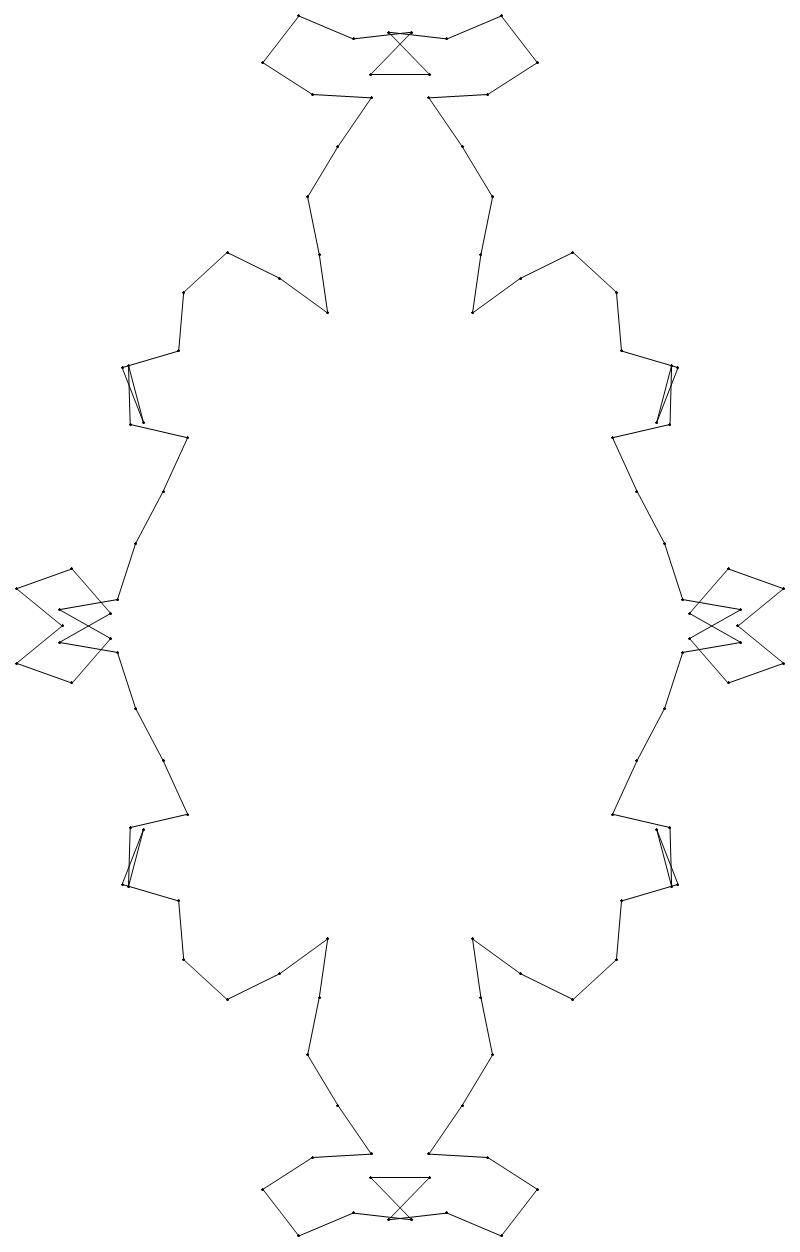
54   45   36   27   18   9

53   44   35   26   17   8

52   43   34   25   16   7

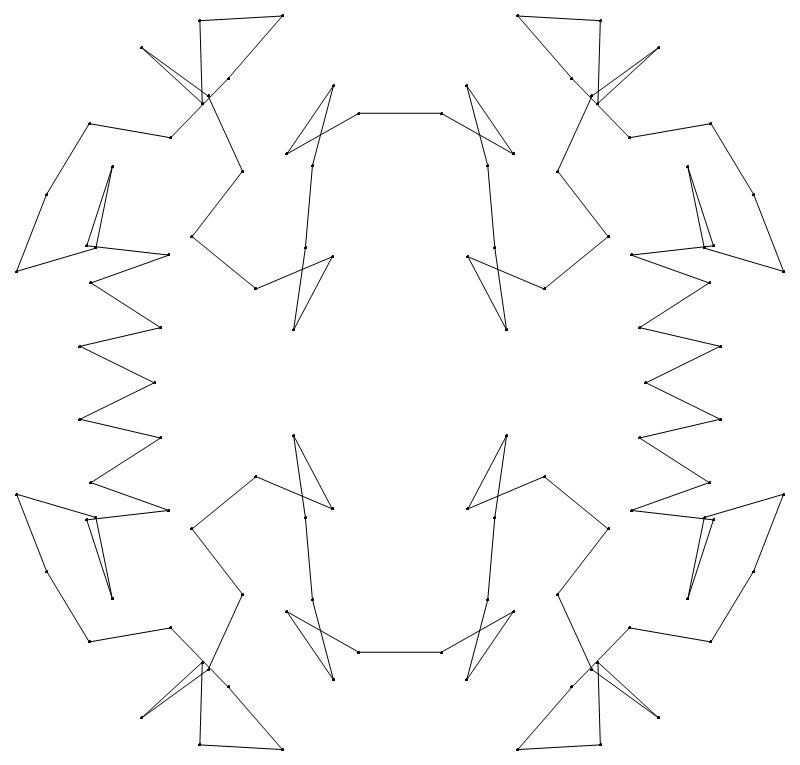
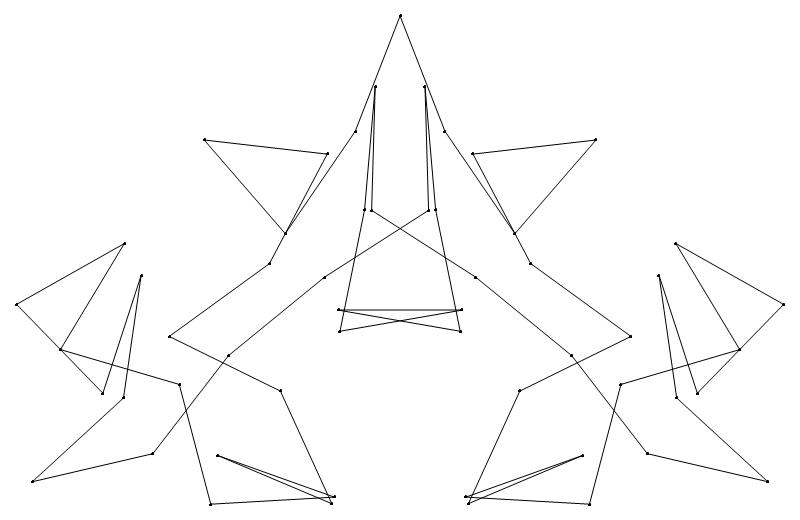
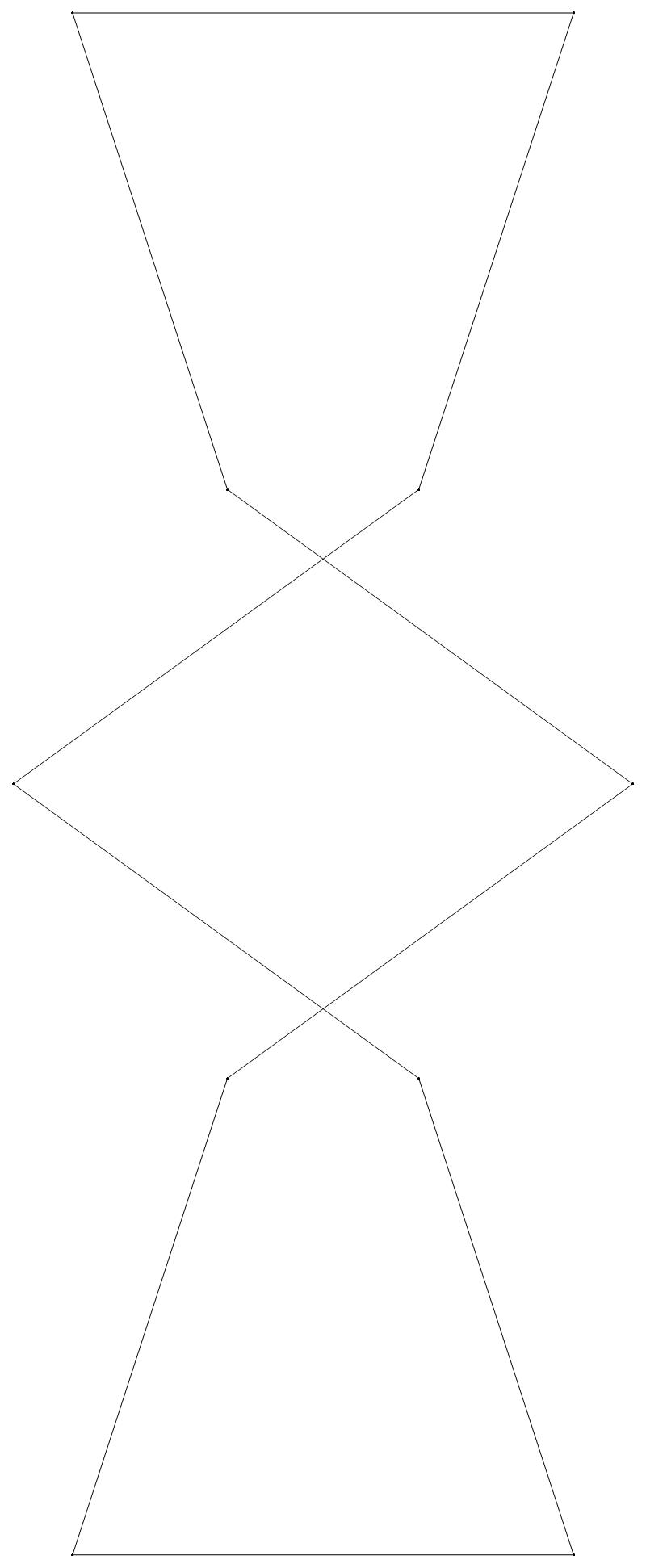
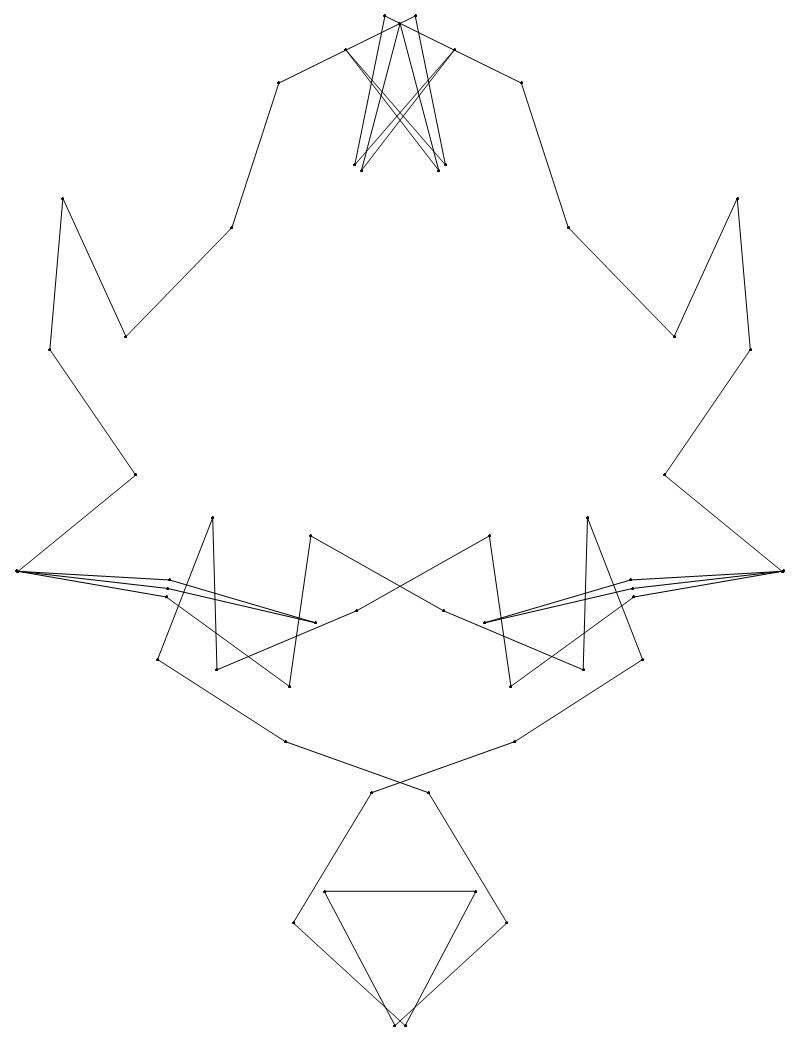
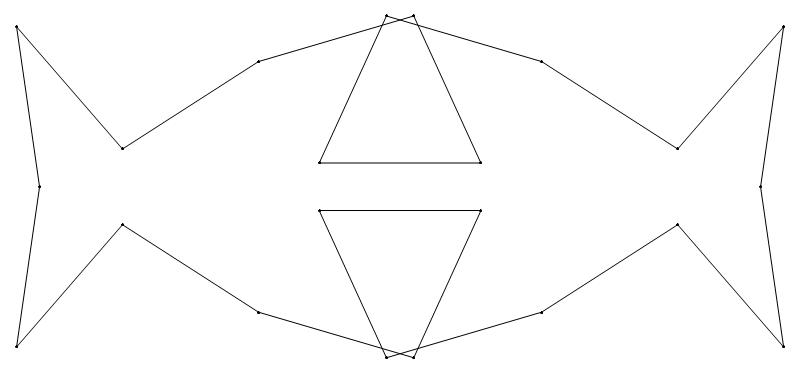
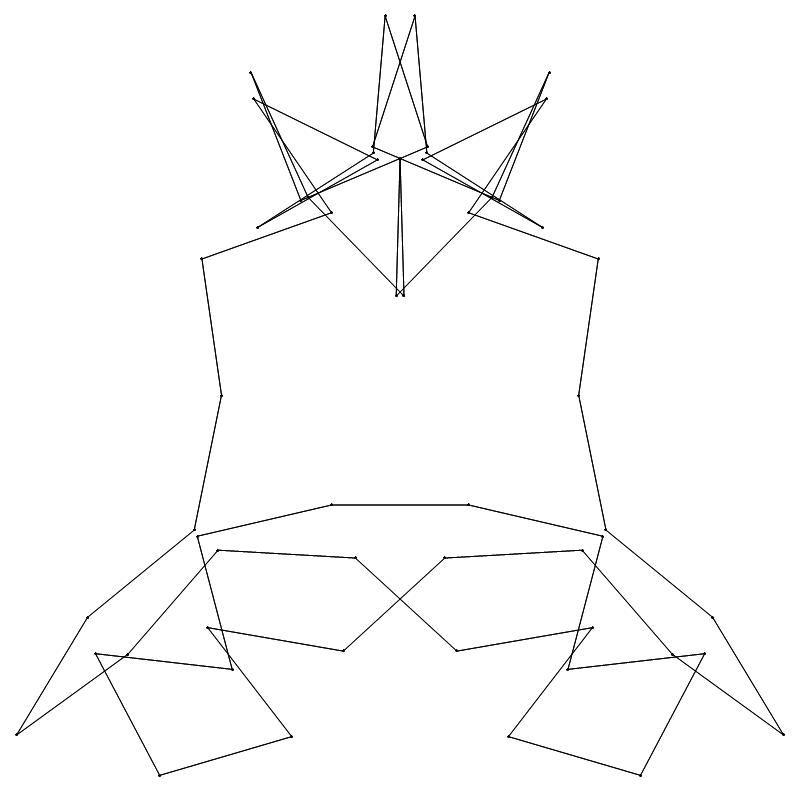
51   42   33   24   15   6

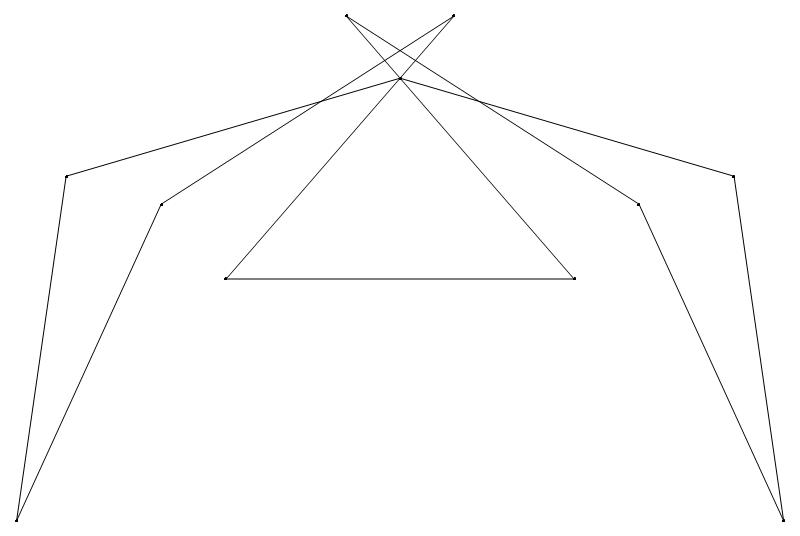
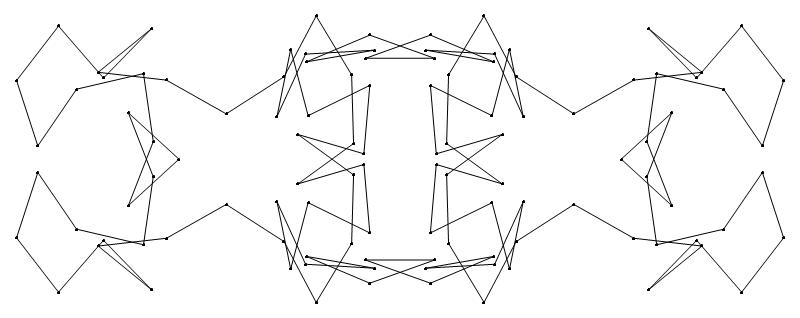
50   41   32   23   14   5

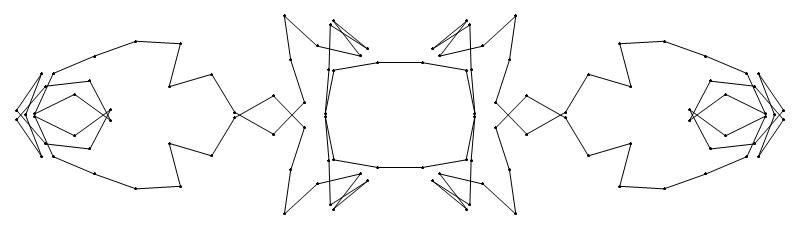
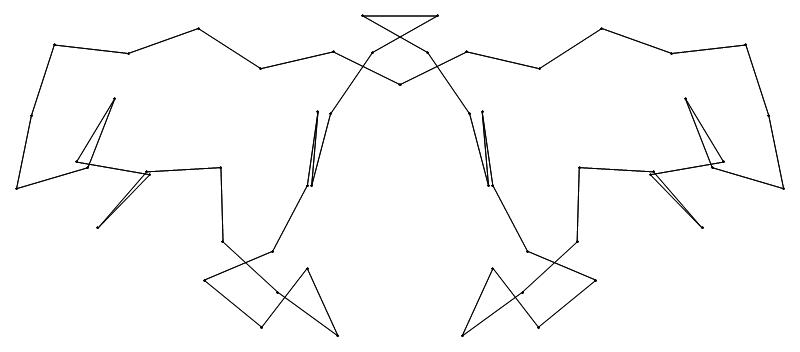
49   40   31   22   13   4

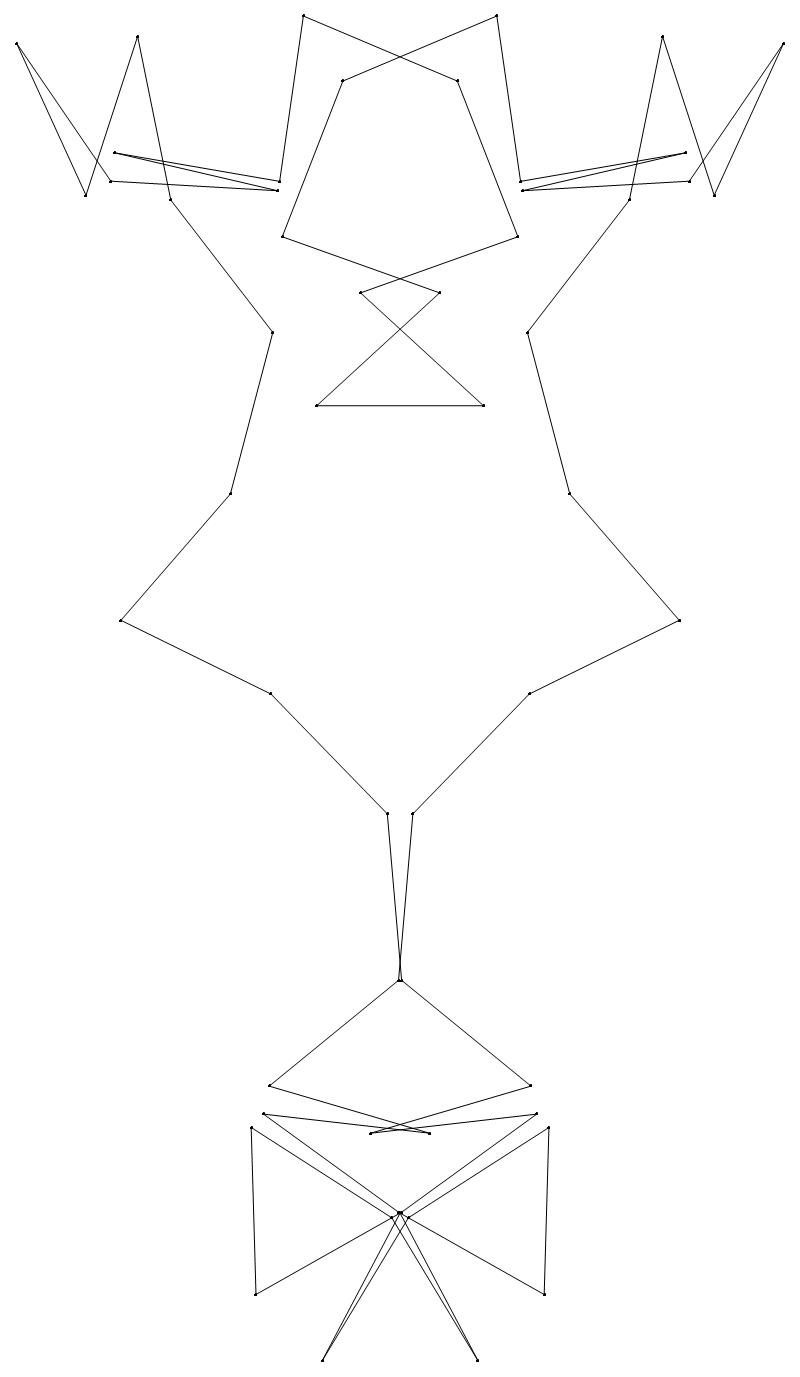
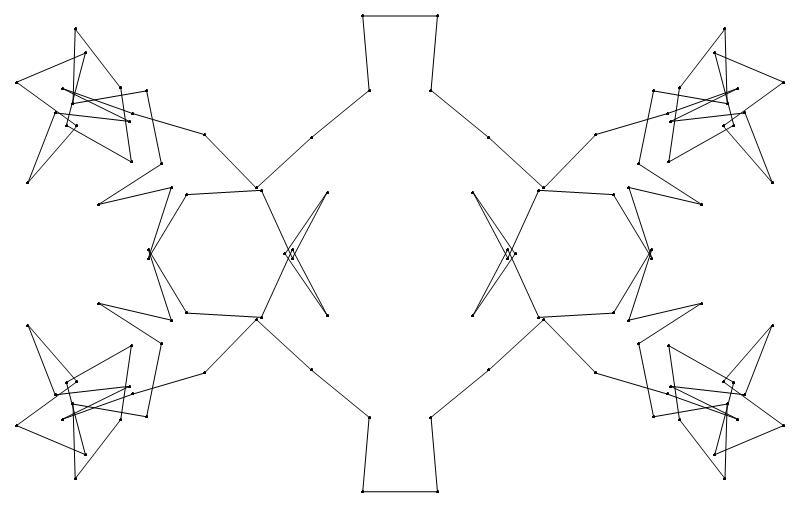
48   39   30   21   12   3

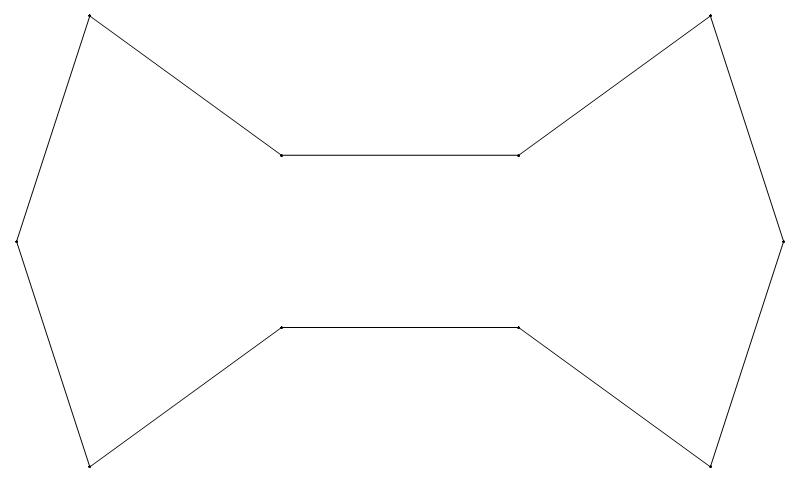
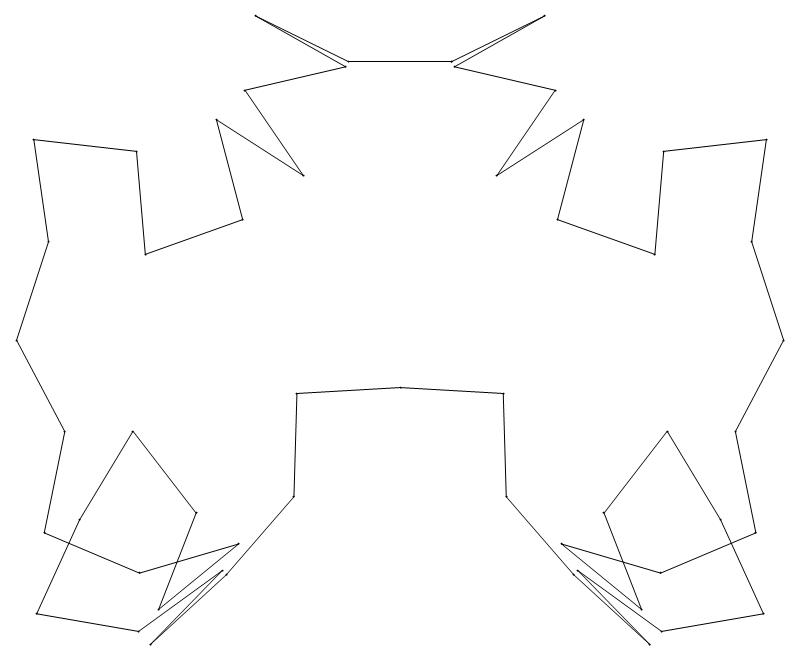
47   38   29   20   11   2

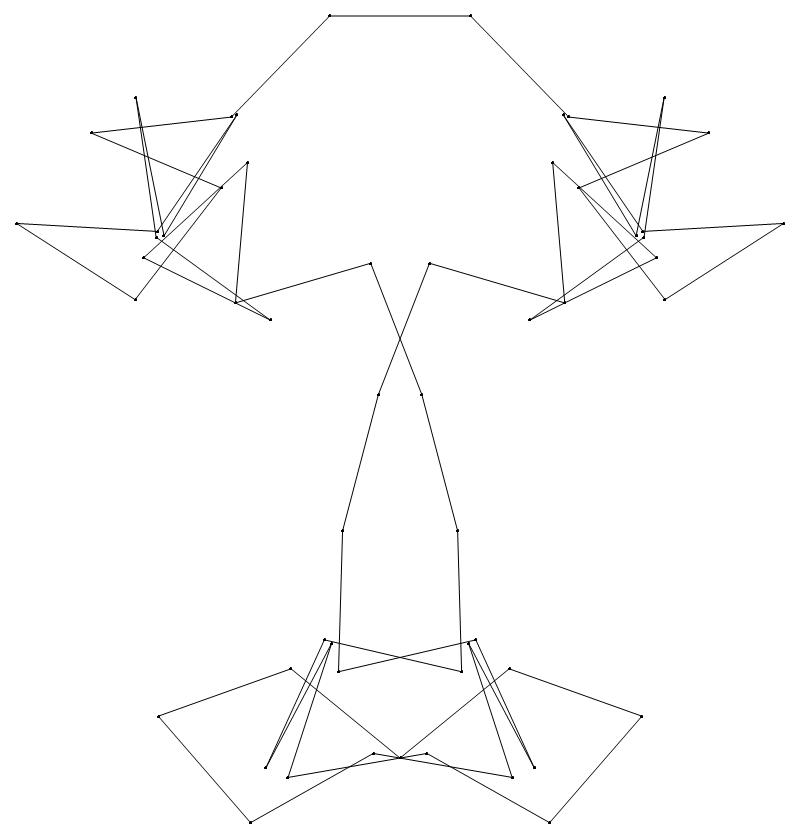
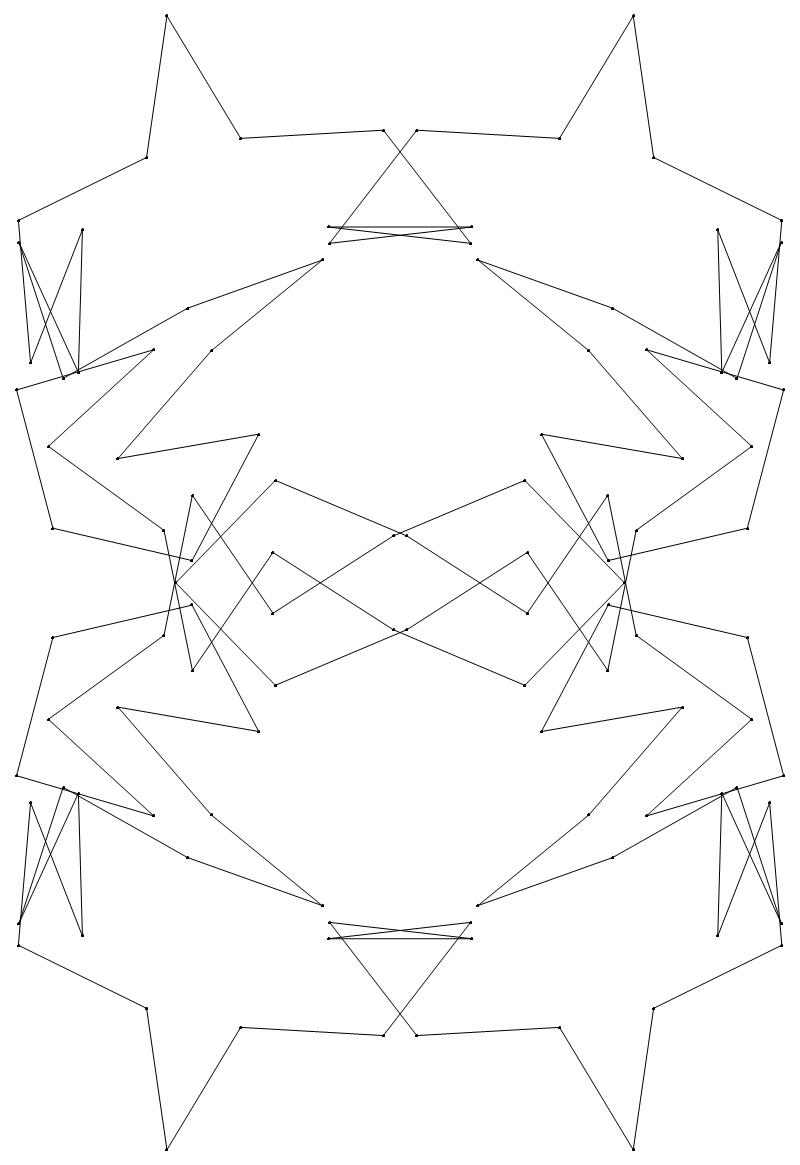
46   37   28   19   10   1

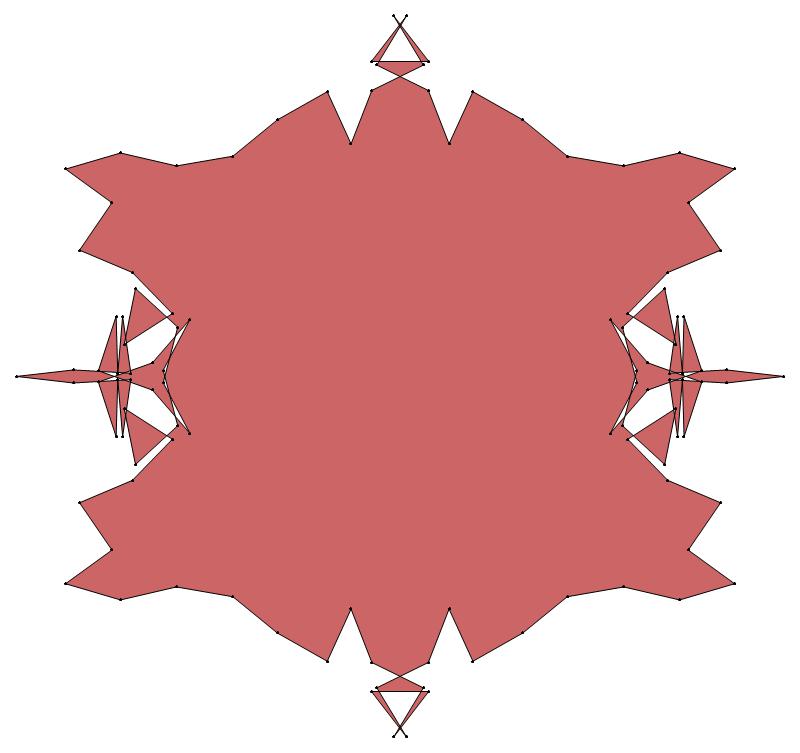
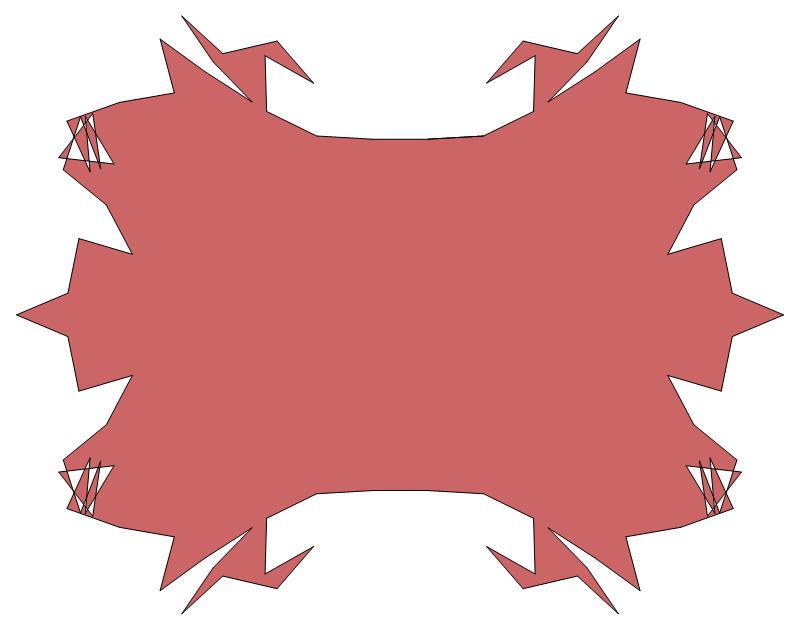
(b) colored
ν has the same value for all images of the same color.

54   45   36   27   18   9

53   44   35   26   17   8

52   43   34   25   16   7

51   42   33   24   15   6

50   41   32   23   14   5

49   40   31   22   13   4

48   39   30   21   12   3

47   38   29   20   11   2

46   37   28   19   10   1

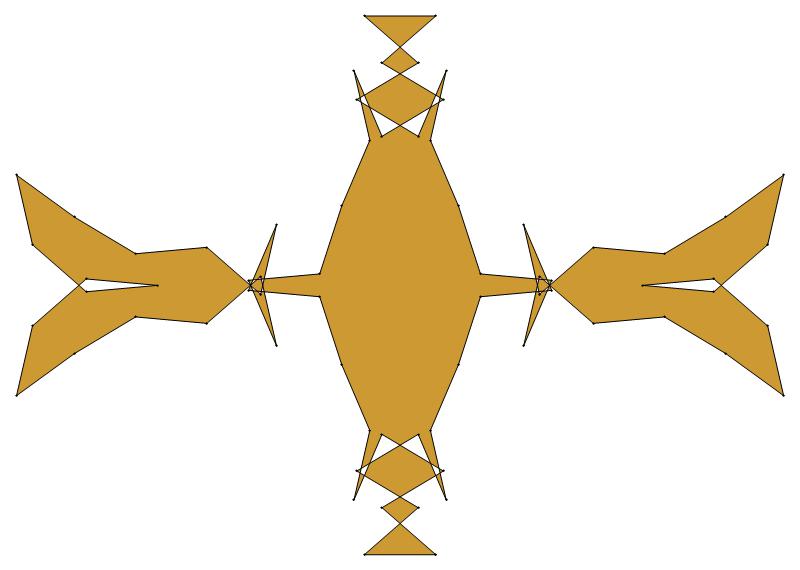
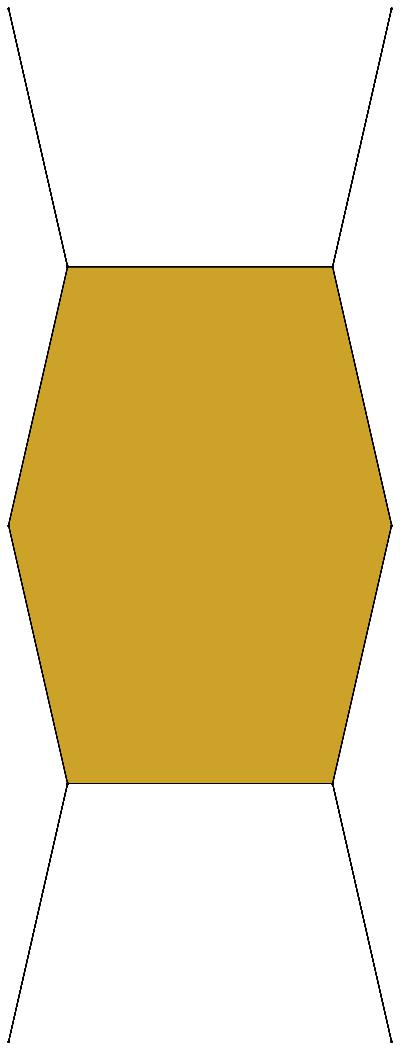
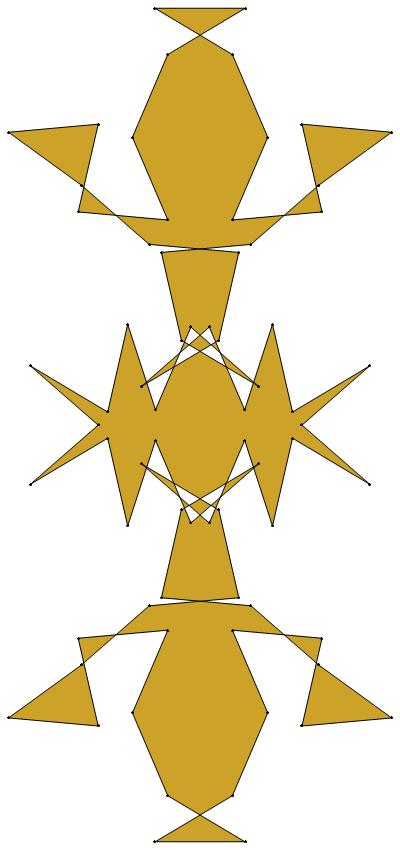
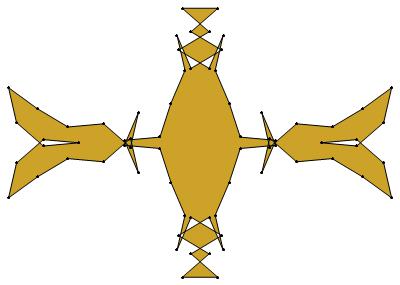
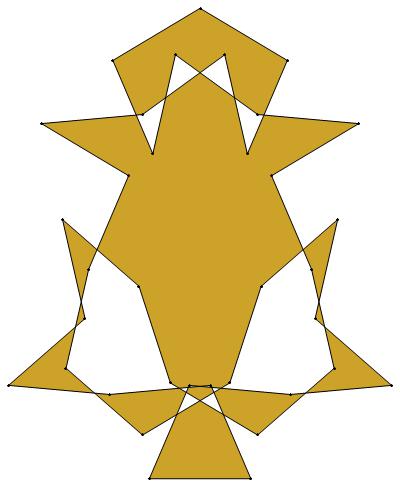
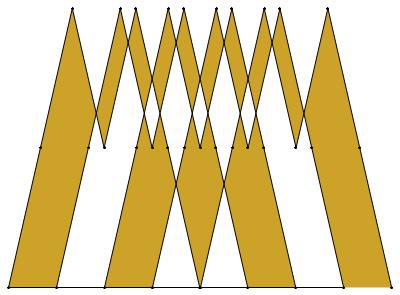
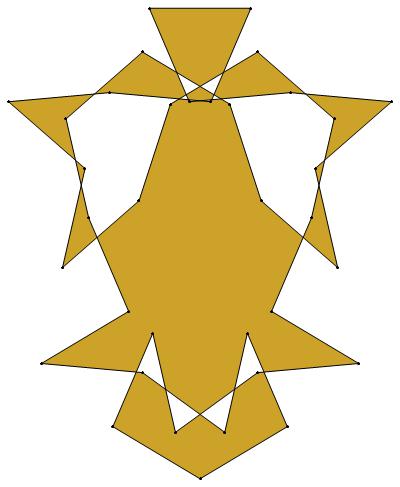
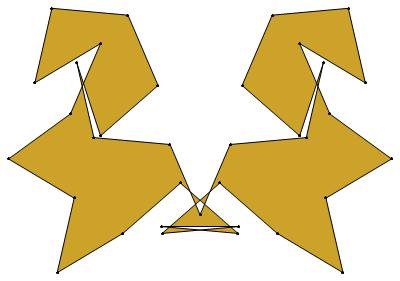
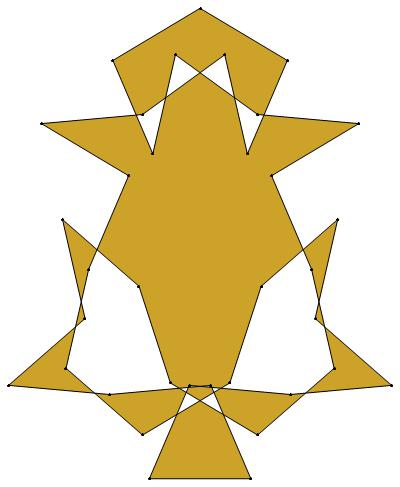
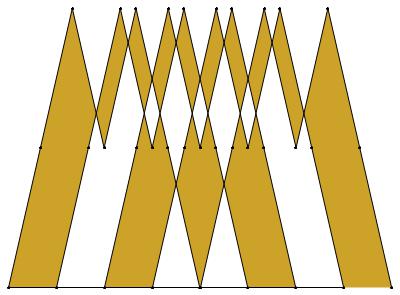
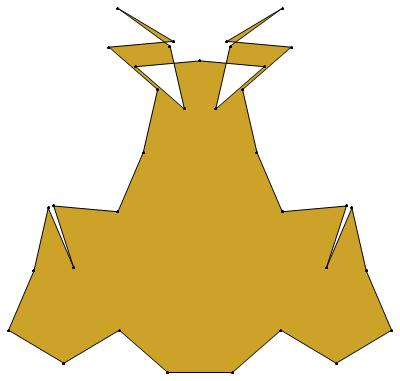
EXAMPLE: (n, α) = (35, 3)
ODD σ

   1    3    5 7 9 11
   13    15    17 19 21 23

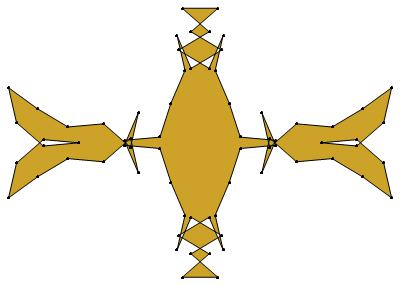
         25 27      29 31 33

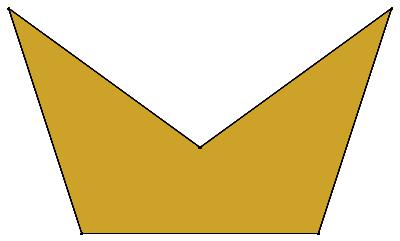
EVEN σ

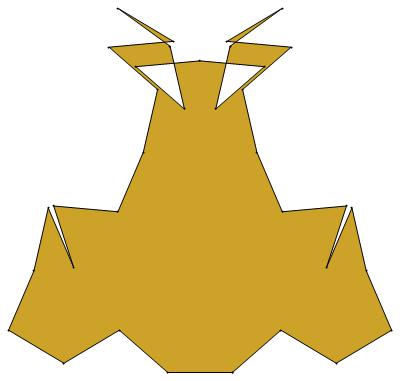
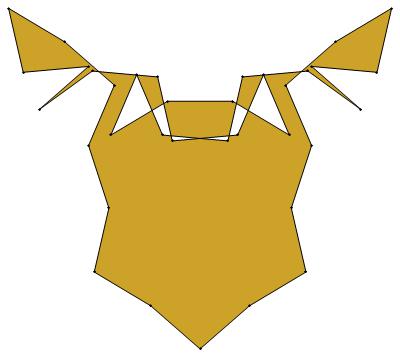
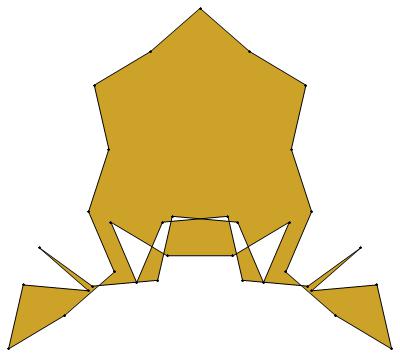
2    4      6 8 10 12

14    16      18   20   22 24
   26    28      30 32 34

EXAMPLE: (n, α) = (15, 3)

ODD σ

   1 3    5   7   9   11    13

EVEN σ

   2 4    6   8   10    12    14

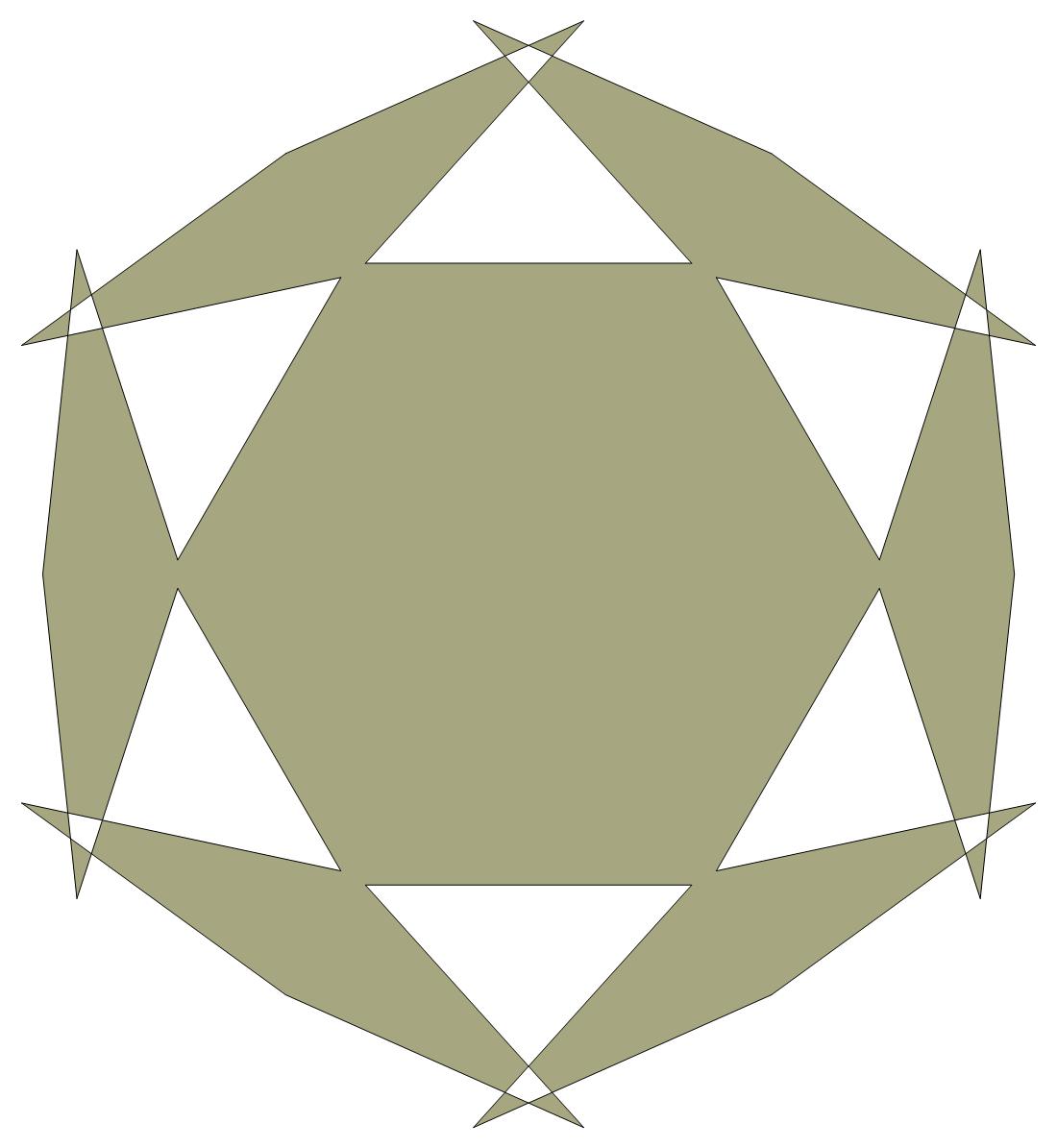
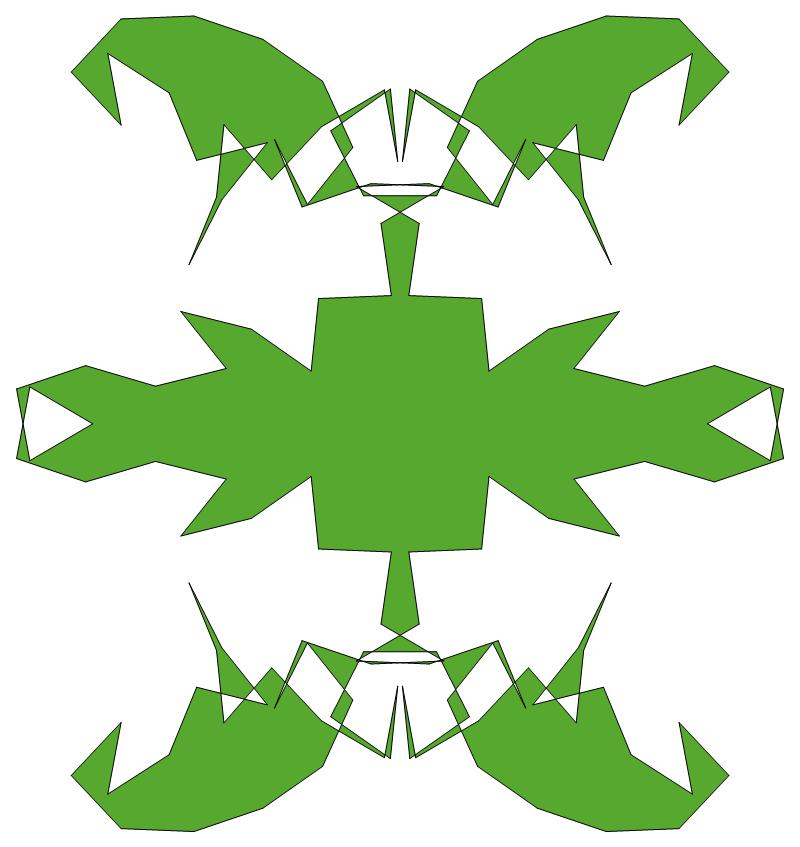
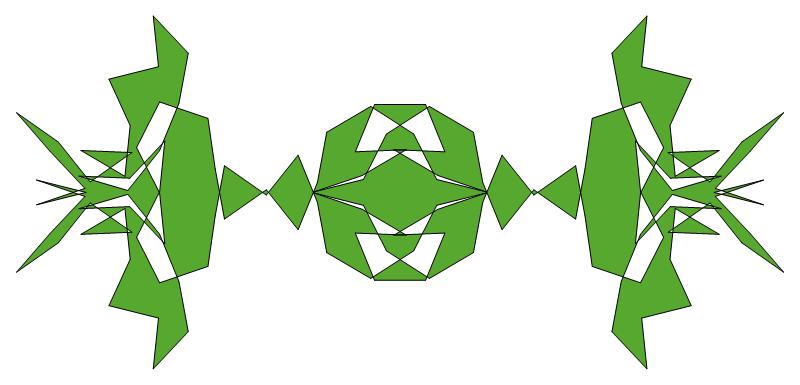
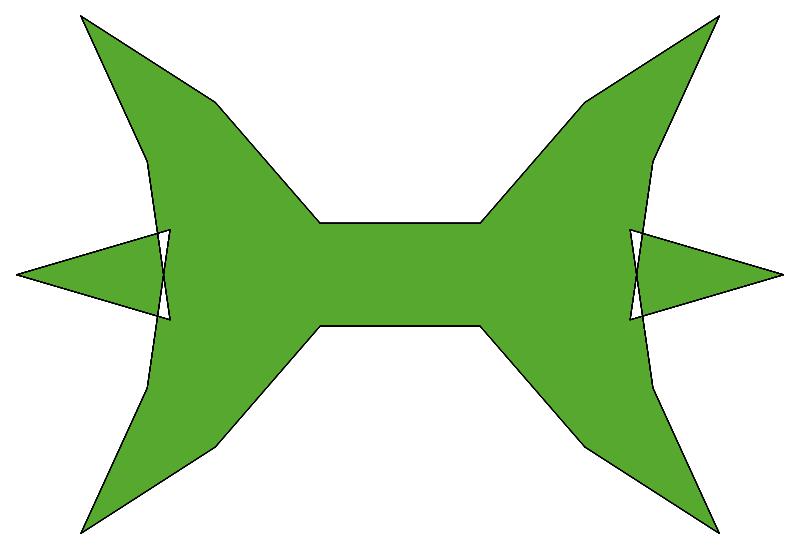
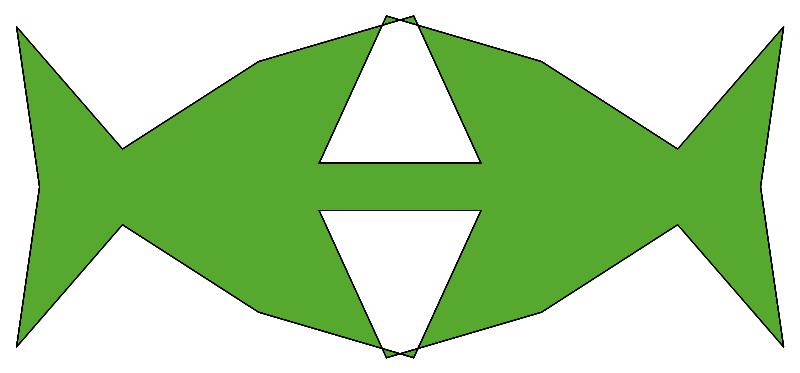
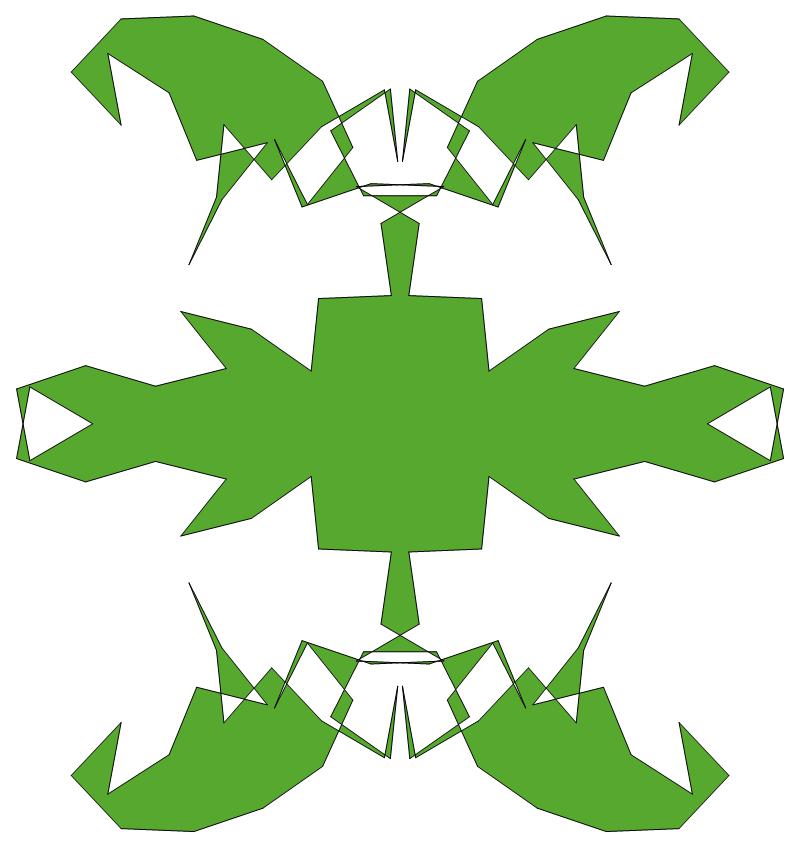
EXAMPLE: (n, α) = (77, 3)

ODD σ

1    3       5 7    9    11

   13    15      17   19 21   23

25    27      29   31   33    35

37    39      41   43   45 47

49    51      53   55   57    59

61    63      65   67   69 71

          73    75

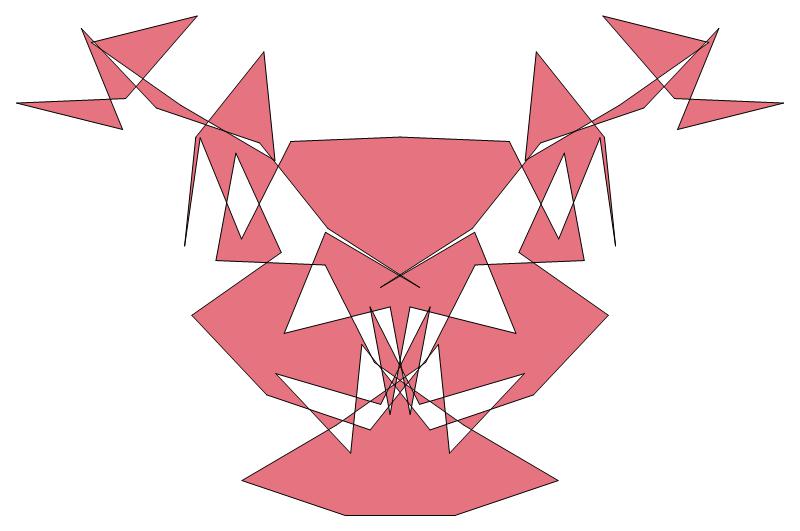
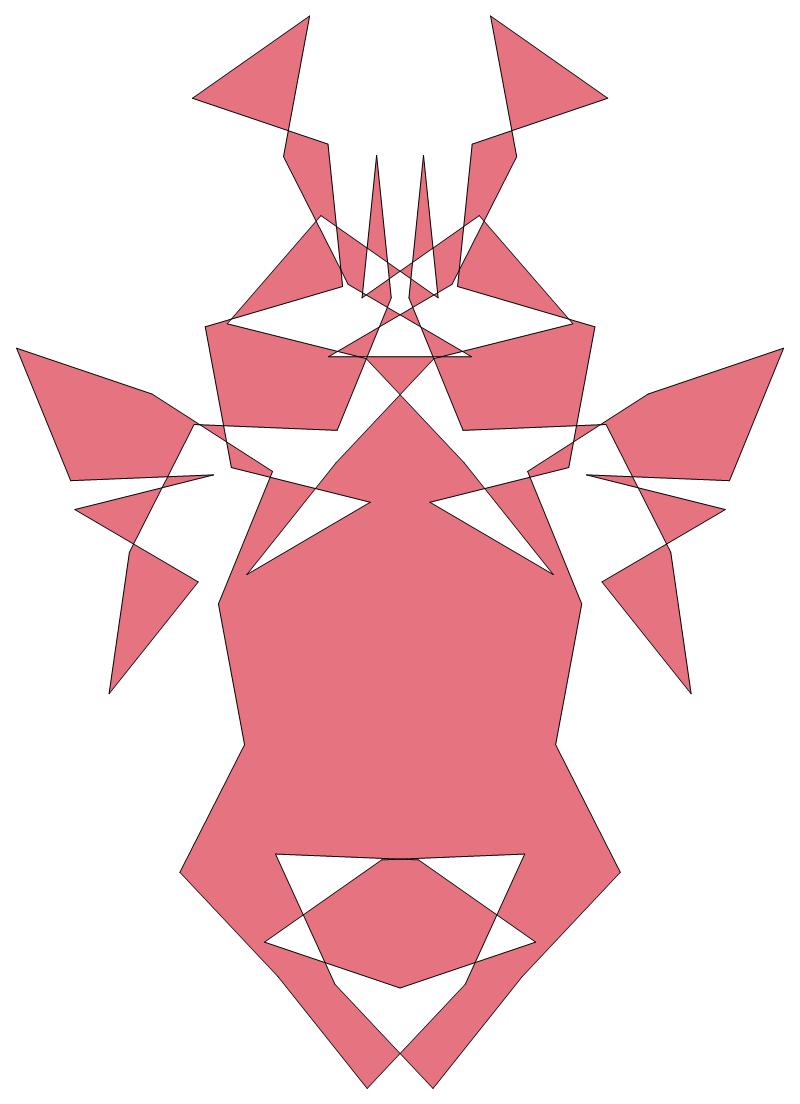
EVEN σ

2    4       6 8    10    12

   14    16      18   20 22   24

26    28      30   32   34    36

38    40      42   44    46 48

50    52      54   56   58    60

62    64      66   68   70 72

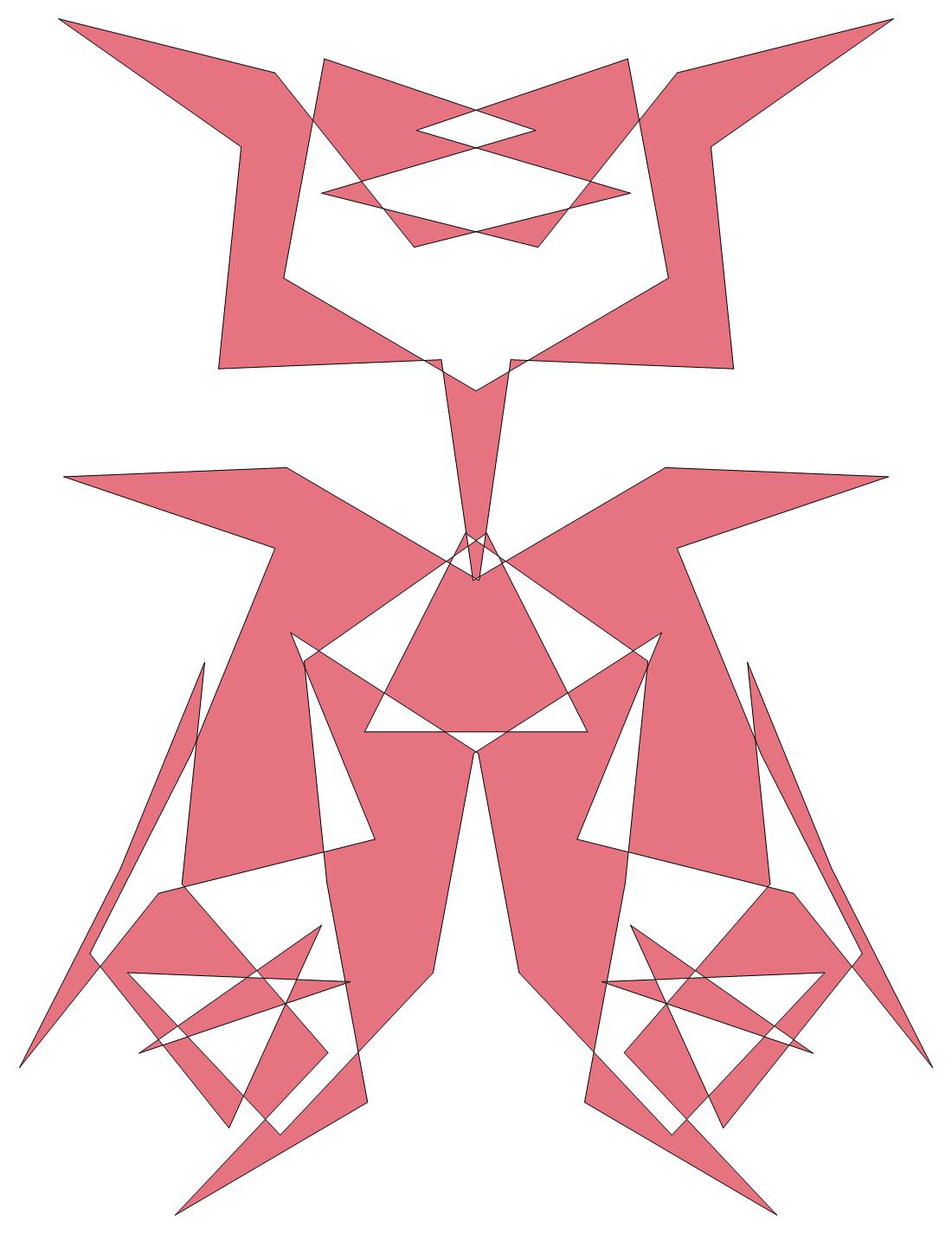
          74    76

A 'Cat's Cradle'

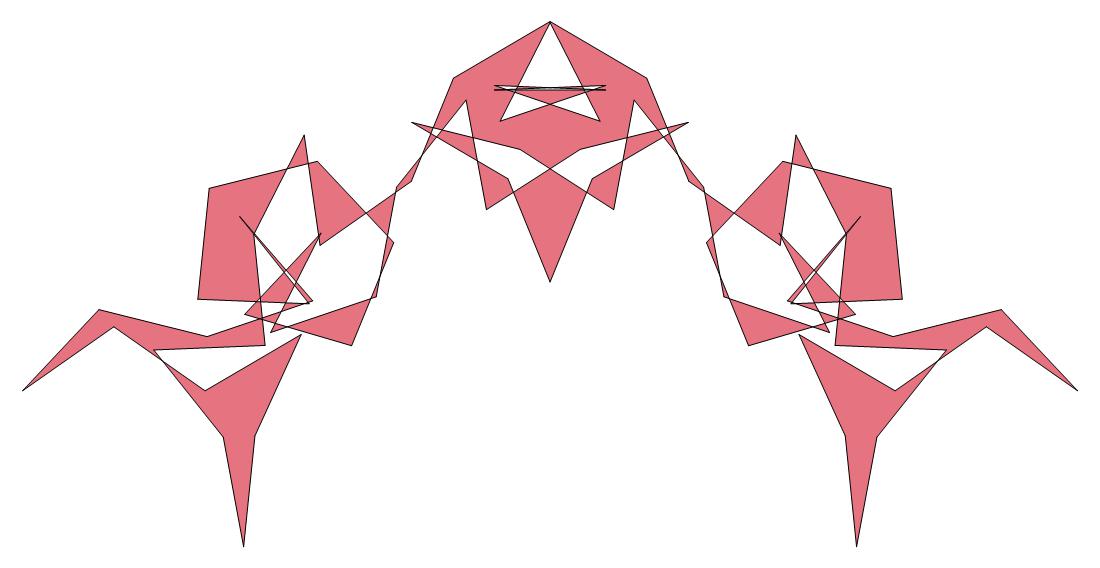
Three examples of 'Decorated Cycloids'

(n, α, σ) = (75, 3, 49)
ν=7350

CATALOG OF SELECTED IMAGES (1986)

Of the three integers labeling each image in this catalog,
the first is the exponent α,
the second is the [loop] step σ, and
the third is the modulus n.
Part 2
Part 3
Part 4
Part 5
Part 6
Part 7
Part 8
Part 9
Part 10
   The image sets in Parts 2 to 8 were generated (in 1983) with a
a FORTRAN program on a mainframe computer.
The image set in Part 9 was generated with a MATHEMATICA
notebook. It is composed of a sequence of 33 images for
modulus n = 65,
exponent α = 3, and
step σ = 1, 3, 5, ..., 63, 65.
   The image set in Part 10 was generated with a MATHEMATICA
notebook. It is composed of a sequence of 10 images for
   modulus n = 3,5,7,11,13,17,19,23,29,31,
exponent α = modulus, and
step σ = 4.

The variety of K-patterns is unlimited.
Below are many examples of
CAT'S CRADLE and
DECORATED CYCLOID
patterns.

CAT'S CRADLE family
                     n = p³ (p = odd prime),
α = p, and
       σ = odd integer.

If σ = k p (k = odd integer), the pattern is defined as the trivial
pattern, because it consists of a single horizontal unit vector.
If σ ≠ k p (k = odd integer), the pattern is called non-trivial.
It contains 2p² unit vectors and has d2 symmetry. There are
two lines of reflection — one horizontal and the other vertical.
There are altogether p(p − 1)/2 non-trivial patterns, each
composed of two interlaced sub-patterns L and R, which are
congruent and have dp symmetry. Each sub-pattern is rotated
about its center by the angle π/p with respect to the other.
L and R each contain p congruent replicas of a pattern motif M,
a d1-symmetric chain of p − 1 unit vectors, centered at angular
    positions that are uniformly distributed around the respective centers
   of L and R. Each replica of M in L(R) is joined at either end by
a horizontal unit vector to a replica of M in R(L). Consecutive
instances of these linking vectors are oppositely directed.

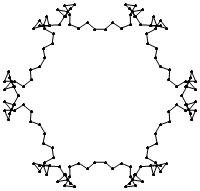
Below is a CAT'S CRADLE pattern for (p, σ, j₀) = (11,1,0).
   Both the set S_red of eleven red instances of the ten-vector motif M
and the set S_green of eleven green instances of M have d11 symmetry.
Every vertex of the red dashed regular 11-gon coincides with the
midpoint of one of the red 10-vector pattern motifs of the frieze, and
   every vertex of the green dashed regular 11-gon coincides with the
midpoint of one of the green 10-vector pattern motifs of the frieze.
The red and green sub-patterns are congruent, but each is rotated
about its center by the angle π/p with respect to the other
and their centers are separated by a horizontal unit vector.

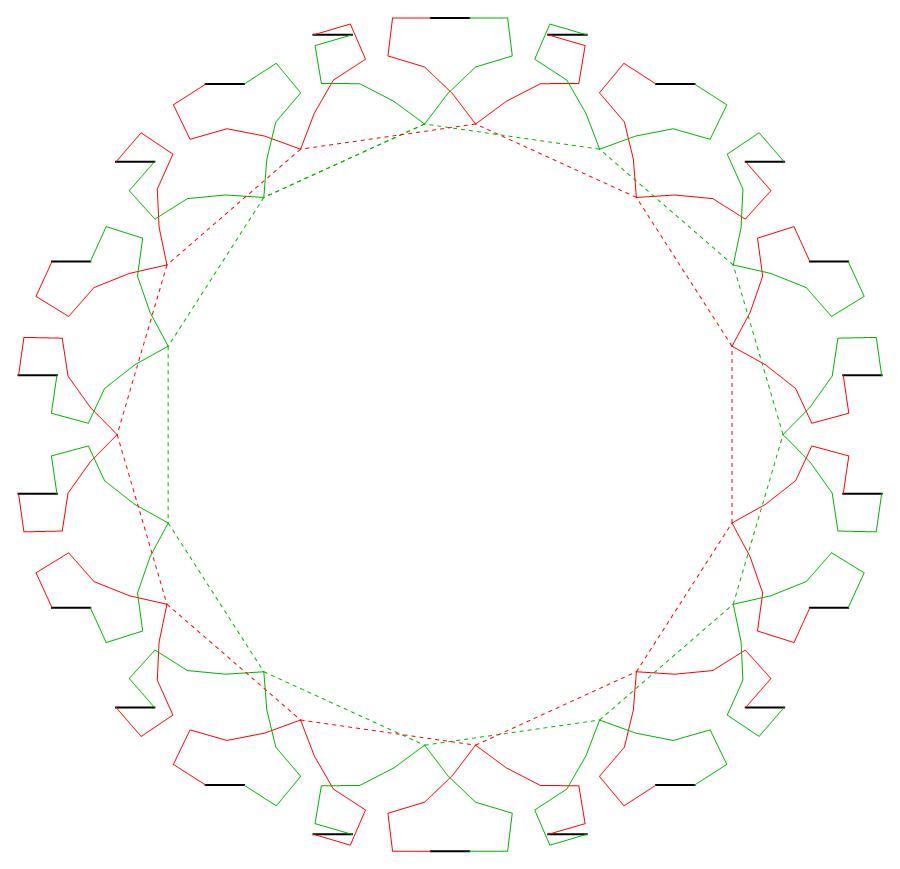
CAT'S CRADLE pattern for (p, σ, j₀) = (11,1,0)

   DECORATED CYCLOID family
           n = p³ (p = odd prime),
α = p, and
                                                                            σ = even integer from the set {2, 4, 6, ..., p(p − 3)/2, p(p − 1)/2}.

    For each odd prime p, there are p(p − 1)/2 non-trivial
frieze patterns — one for each even step σ:

If σ = k p (k = even integer), the pattern is trivial.
It contains a single horizontal unit vector.
   If σ ≠ k p , the pattern is composed of a linear chain of
   congruent pattern motifs M, each of which is comprised
    of p − 1 unit vectors and has d1 symmetry. Each replica
of M is joined at either end to another replica of M by a
   horizontal unit linking vector. The linking vectors are
all pointed in the same direction (left or right).
      As described below, the vertices at the centers of all the
   instances of M lie on a single cycloid — hence the
family name, 'DECORATED CYCLOID'.
The parametric equations for the prolate cycloid are:
x = a φ − b sin φ
y = a − b cosφ,
b > a.

There are 61 odd primes p < 300.
Here is an ordered sequence of 61 images — one for each of these 61 primes —
of the (p-1)-vector pattern motif M of a DECORATED CYCLOID frieze pattern.
The parameter set (n, α, σ, j₀) for each of these DECORATED CYCLOIDS is (p, p, 2, 0).

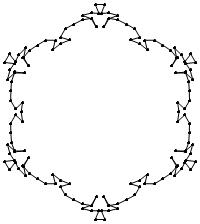
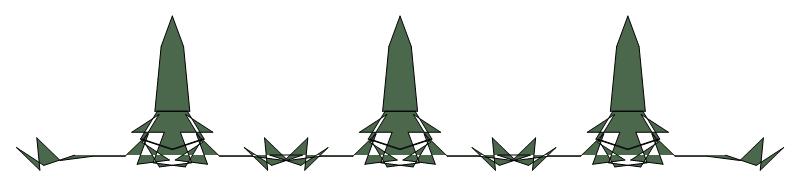
Below is a DECORATED CYCLOID frieze for (p, σ, j₀) = (11,2,0).

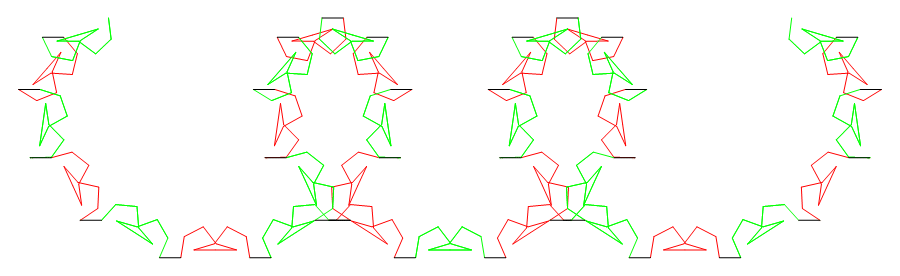
Just as in the CAT'S CRADLE for (p, σ, j₀) = (11,1,0) shown above,
every red or green ten-vector pattern motif M has d1 symmetry, but
in these patterns, the center of every motif lies on the same curve, a
prolate cycloid. The horizontal unit vectors that join red and green
motifs all have a common direction — to the right. All instances of
the motif M are related by composition of (a) rotation by an integer
multiple of π/m about the center of a common circle and (b) translation
to the right by an integer number of unit vectors.
John H. Conway has invented a new symbol for the symmetry of frieze
patterns that have two parallel lines of reflection (he calls this symmetry 'sidle'):

(cf. p. 68 of 'The SYMMETRIES of THINGS',
by Conway, Burgiel, and Goodman-Strauss,
A.K. Peters, Ltd, 2008).

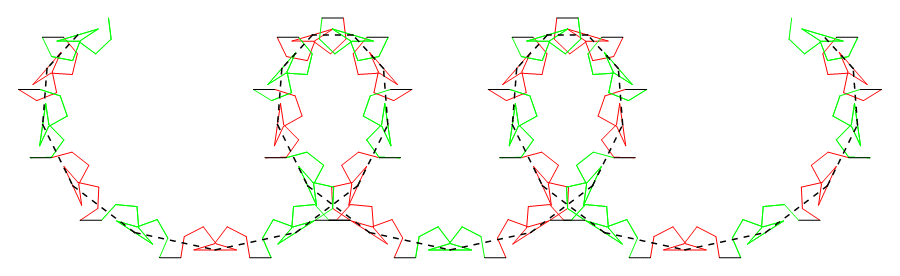
Click here for an enlarged view of this CAT'S CRADLE image — (p, σ, j₀) = (11,1,0)
The dashed chords join those vertices in the pattern that lie exactly on the corresponding cycloid (just below).

Click here for an enlarged view of this image

Corresponding to every CAT'S CRADLE or DECORATED CYCLOID pattern,
there exists a simpler unlinked centro-symmetric pattern of d2p symmetry based
on the same motif M. In these unlinked patterns, there are no linking vectors, and
the motifs in each of the two interlaced motif subsets are located at the same radial
distance from the center of the pattern. The central angles of consecutive instances
of the motif differ by Δθ = σ π/p (mod 2π).

Below — at the right — is the complete set of three
non-trivial CAT'S CRADLE patterns for p = 3. At
the left is the associated unlinked d6-symmetric pattern.

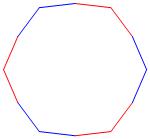
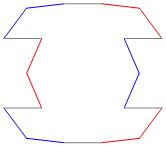
σ = 1     Δθ = 60°

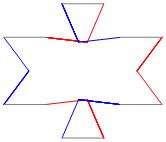
σ = 5     Δθ = − 60°

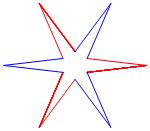
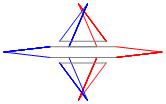
σ = 7     Δθ = 60°

In the right column below is the complete set of twenty-
one non-trivial CAT'S CRADLE patterns for p = 7. In
the left column are the associated unlinked d14 patterns.

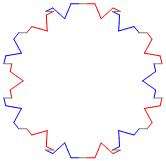
σ = 1     Δθ ≅ π/7

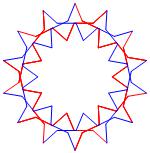
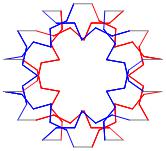
σ = 3     Δθ ≅ 3π/7

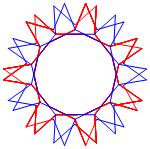
σ = 5     Δθ ≅ 5π/7

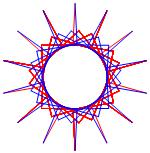
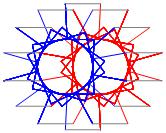
σ = 9     Δθ ≅ − 5π/7

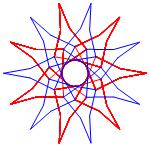
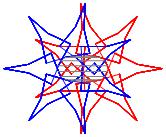
σ = 11     Δθ ≅ − 3π/7

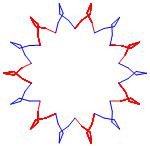
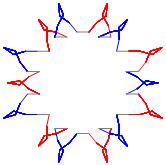
σ = 13     Δθ ≅ − π/7

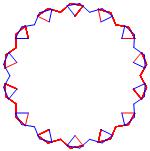
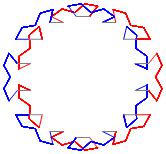
σ = 15     Δθ ≅ π/7

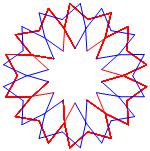
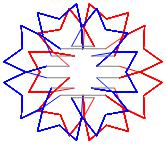
σ = 17     Δθ ≅ 3π/7

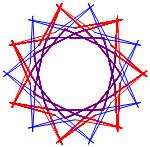
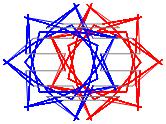
σ = 19     Δθ ≅ 5π/7

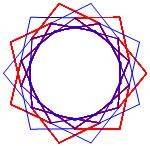
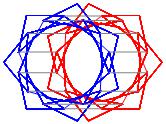
σ = 23     Δθ ≅ − 5π/7

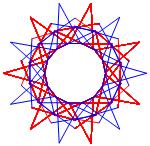
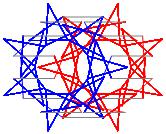
σ = 25     Δθ ≅ − 3π/7

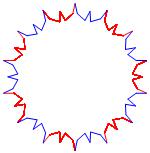
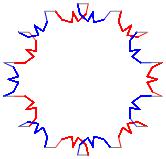
σ = 27    - Δθ ≅ − π/7

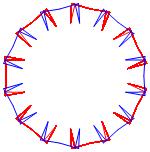
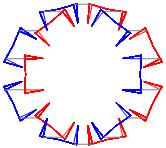
σ = 29     Δθ ≅ π/7

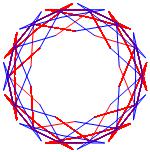
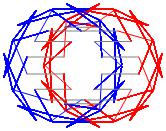
σ = 31     Δθ ≅ 3π/7

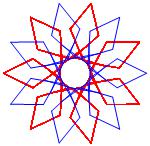
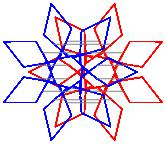
σ = 33     Δθ ≅ 5π/7

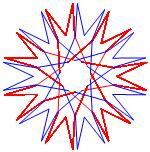
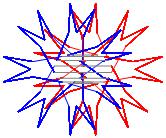
σ = 37     Δθ ≅ − 5π/7

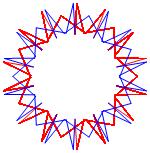
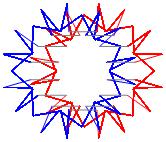
σ = 39     Δθ ≅ − 3π/7

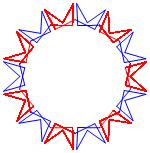
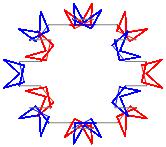
σ = 41     Δθ ≅ −π/7

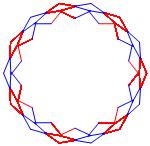
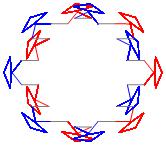
σ = 43     Δθ ≅ π/7

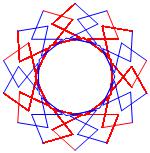
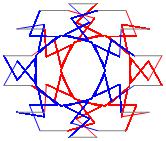
σ = 45     Δθ ≅ 3π/7

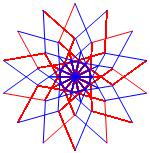
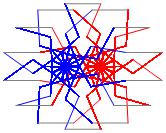
σ = 47     Δθ ≅ 5π/7

CAT'S CRADLE_5
The complete set of 10 non-trivial patterns of CAT'S CRADLE_5 (p = 5):
σ = {1, 3, 7, 9, 11, 13, 17, 19, 21, 23}.
The entire ten-pattern sequence is displayed eight times.
The pattern for σ_50k+j (j, k = 1, 2, 3,...) is identical to the pattern for σ_j.
To animate the sequence, hold down the 'PageDown' key.
Here this set of ten patterns is shown in two colors.

CAT'S CRADLE_7
The complete set of the 21 non-trivial patterns of CAT'S CRADLE_7 (p = 7):
σ = {1, 3, 5, 9, 11, 13, 15, 17, 19, 23, 25, 27, 29, 31, 33, 37, 39, 41, 43, 45, 47}.
The pattern for σ_98k+j (j, k = 1, 2, 3,...) is identical to the pattern for σ_j, and
the pattern for σ_49k+j (j, k = 1, 2, 3,...) is identical to the pattern for σ_49k−j.
Here's an alternative way to show the detailed structure of these patterns:
For σ ≠ 7k (k=1,2,...), the complete image is followed by a d7-symmetric
unlinked image of one-half of the complete pattern, comprising a set of
seven replicas of the six-edged pattern motif M. The horizontal linking
vectors are omitted from this image, but a colored stellated heptagon
{p/q} is inscribed, with each vertex located at the center of one of the
seven replicas of the pattern motif. The polygon density (also known
as the winding number) of each heptagon is determined simply by the
angular positions of the centers of the seven replicas of the pattern motif,
   which are governed by the order in which the edges of the pattern are drawn.
By inspecting these patterns you can readily confirm that the 'q' in {p/q}
is equal to σ (mod 7). (The proof is short and simple. Do you recognize it?)

To animate these sequences, hold down the 'PageDown' key.

CAT'S CRADLE_13
The complete set of 78 non-trivial patterns of CAT'S CRADLE_13 (p = 13):
σ = {1, 3, 5, 7, 9, 11, 15, 17, ..., 165, 167}.
To animate the sequence, hold down the 'PageDown' key.

CAT'S CRADLE_17
The first 128 patterns of CAT'S CRADLE_17 (p = 17):
σ = {1, 3, 5, ..., 253, 255}.
Included are 7 instances of the trivial pattern.
(The complete set contains 136 distinct non-trival patterns.)
To animate the sequence, hold down the 'PageDown' key.

CAT'S CRADLE_47
The first 48 patterns of CAT'S CRADLE_47 (p = 47):
σ = {1, 3, ..., 93}.
Included is one instance of the trivial pattern.
(The complete set contains 1081 non-trival patterns.)
To animate the sequence, hold down the 'PageDown' key.
You may need to
(a) adjust the ZOOM value to 100%
and then
(b) center the images on the screen.

DECORATED CYCLOID_5
The complete set of 10 non-trivial patterns for DECORATED CYCLOID_5 (p=5):
σ = {2, 4, 6, 8, 12, 14, 16, 18, 22, 24}.
Each pattern is shown eight times.
The pattern for σ_50k+j (j, k = 1, 2, 3,...) is identical to the pattern for σ_j.
To animate the sequence, hold down the 'PageDown' key.

DECORATED CYCLOID_7
The first 21 non-trivial patterns for DECORATED CYCLOID_7 (p=7)
σ = {2, 4, 6, 8, 12, 14, 16, 18, 22, ..., 46, 48}.
The pattern for σ_98k+j (j, k = 1, 2, 3,...) is identical to the pattern for σ_j.
To animate the sequence, hold down the 'PageDown' key.
DECORATED CYCLOID_7 (complete)
The complete set of 49 patterns for DECORATED CYCLOID_7 (p=7):
σ = {2, 4, 6, ..., 96, 98}.
The red dashed chords join those vertices
that lie on the corresponding cycloid.

The pattern for σ_100k+j (j, k = 1, 2, 3,...) is identical to the pattern for σ_j.
To animate the sequence, hold down the 'PageDown' key.

DECORATED CYCLOID_17
The first 128 patterns of DECORATED CYCLOID_17 (p=17):
σ = {2, 4, ..., 256}.
Included are 7 instances of the trivial pattern.
(The complete set contains 136 distinct non-trival patterns.)
To animate the sequence, hold down the 'PageDown' key.

DECORATED CYCLOID_47
The first 140 patterns of DECORATED CYCLOID_47 (p=47):
σ = {2, 4, ..., 280}.
Included are 3 instances of the trivial pattern.
To animate the sequence, hold down the 'PageDown' key.

Back to GEOMETRY GARRET