Welcome to the
GEOMETRY GARRET!
A Pot-Pourri of People, Pictures, Places, Penrose Patterns, Polyhedra, Polyominoes, Posters, Posies, and Puzzles
Alan H. Schoen
Comments are welcome!

Gyroid Jingle
(Anon.)
Fritz Laves found a crystal net with edges joined by threes,
It twists and turns throughout R3 in perfect helices.
This net has two varieties – to left or right they spiral.
When two are intertwined the combination isn’t chiral.
‘Twixt two such nets a curving surface wends its way through space,
With tunnels everywhere that make it look just like old lace.
Now some do say the cosmos uses pasta (1) as its model.
(If that’s too big a stretch for you, you could just say it’s twaddle.)
R. Wagner wrote some famous operas, staging them at Bayreuth
(A name with several rhyming words – there’s thyroid and there’s gyroid).
And that’s the name by which we know this anticlastic surface,
Whose labyrinths are such a maze they’re bound to make you nervous.
We hear that gyroid shapes are formed in heav’n in some stars.
(There’s no report that this occurs on Venus or on Mars.)
Such stars are not the common types like Capricorn or Castor,
But rather they’re like neutron stars (which spin around much faster).
Since many words do rhyme with ‘G’, like brie and ghee and plea,
To simplify this verse we’ll call the gyroid simply G.
Schwarz, Weierstrass, and Riemann taught us long ago to see
That G’s the offspring of two others known as P and D.
There’s Single G and Double G. Which one do you like more?
Since both occur in Nature, there’s no point in keeping score.
(2) Luzzati found that Double G can crystallize as soap,
And in the soap domain he’s known world over as the Pope.
Cosmologists say the universe arose by chance – not purpose.
So we conclude the gyroid’s just an accidental surface.
Vittorio2 found its structure hidden in a plain detergent.
And now phenomena like this are properly called emergent.
1. Appearance of the Single Gyroid Network Phase in Nuclear Pasta Matter,
arXiv:1404.4760v5 [nucl-th] 31 Oct 2014, B. Schuetrumpf, M. A. Klatt,
K. Iida, G. E. Schroeder-Turk, J. A. Maruhn, K. Mecke, P.-G. Reinhard








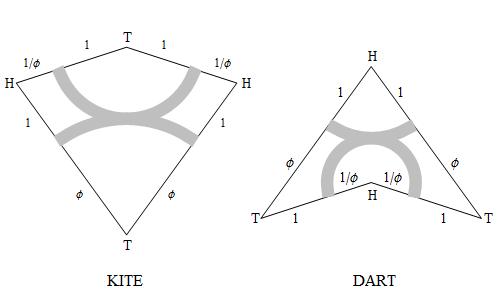
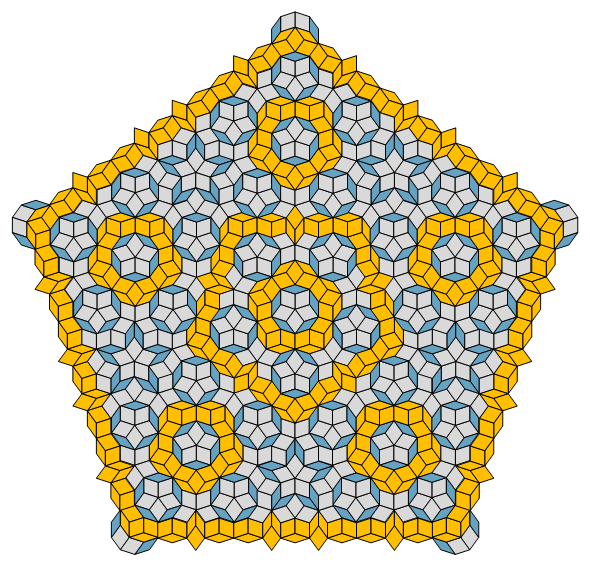

grid.gif)

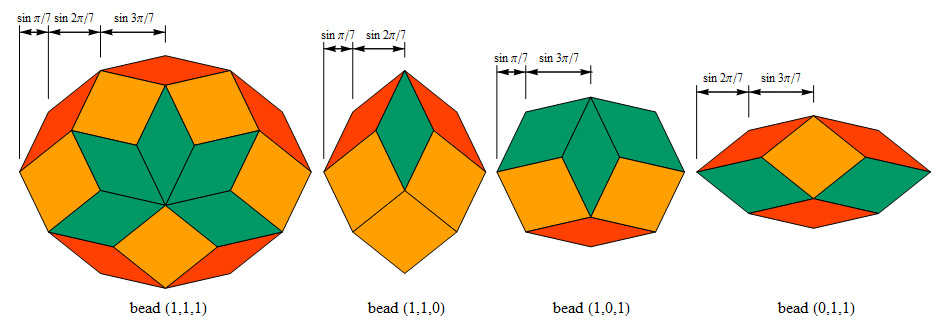


_thumbnail_reduced.jpg)
_thumbnail_reduced.jpg)
_thumbnail_reduced.jpg)





.jpg)








_thumbnail_reduced.jpg)









_in_clearboxes_thumbnail_reduced.jpg)
_in_clearboxes(2)_thumbnail_reduced.jpg)
_twopieces_thumbnail_reduced.jpg)


_[111]_thumbnail_reduced.jpg)
.jpg)








.jpg)









.jpg)
.jpg)
.jpg)
_thumbnail_reduced.jpg)





_thumbnail_reduced.jpg)

